Cosmological Analysis with Calibrated Neural Quantile Estimation and Approximate Simulators

A major challenge in extracting information from current and upcoming surveys of cosmological Large-Scale Structure (LSS) is the limited availability of computationally expensive high-fidelity simulations. We introduce Neural Quantile Estimation (NQE), a new Simulation-Based Inference (SBI) method that leverages a large number of approximate simulations for training and a small number of high-fidelity simulations for calibration. This approach guarantees an unbiased posterior and achieves near-optimal constraining power when the approximate simulations are reasonably accurate. As a proof of concept, we demonstrate that cosmological parameters can be inferred at field level from projected 2-dim dark matter density maps up to $k_{\rm max}\sim1.5\,h$/Mpc at $z=0$ by training on $\sim10^4$ Particle-Mesh (PM) simulations with transfer function correction and calibrating with $\sim10^2$ Particle-Particle (PP) simulations. The calibrated posteriors closely match those obtained by directly training on $\sim10^4$ expensive PP simulations, but at a fraction of the computational cost. Our method offers a practical and scalable framework for SBI of cosmological LSS, enabling precise inference across vast volumes and down to small scales.

Simulation-Based Inference with Quantile Regression

We present Neural Quantile Estimation (NQE), a novel Simulation-Based Inference (SBI) method based on conditional quantile regression. NQE autoregressively learns individual one dimensional quantiles for each posterior dimension, conditioned on the data and previous posterior dimensions. Posterior samples are obtained by interpolating the predicted quantiles using monotonic cubic Hermite spline, with specific treatment for the tail behavior and multi-modal distributions. We introduce an alternative definition for the Bayesian credible region using the local Cumulative Density Function (CDF), offering substantially faster evaluation than the traditional Highest Posterior Density Region (HPDR). In case of limited simulation budget and/or known model misspecification, a post-processing broadening step can be integrated into NQE to ensure the unbiasedness of the posterior estimation with negligible additional computational cost. We demonstrate that the proposed NQE method achieves state-of-the-art performance on a variety of benchmark problems.

Beyond Moments: Robustly Learning Affine Transformations with Asymptotically Optimal Error

We present a polynomial-time algorithm for robustly learning an unknown affine transformation of the standard hypercube from samples, an important and well-studied setting for independent component analysis (ICA). Specifically, given an $\epsilon$-corrupted sample from a distribution $D$ obtained by applying an unknown affine transformation $x \rightarrow Ax+s$ to the uniform distribution on a $d$-dimensional hypercube $[-1,1]^d$, our algorithm constructs $\hat{A}, \hat{s}$ such that the total variation distance of the distribution $\hat{D}$ from $D$ is $O(\epsilon)$ using poly$(d)$ time and samples. Total variation distance is the information-theoretically strongest possible notion of distance in our setting and our recovery guarantees in this distance are optimal up to the absolute constant factor multiplying $\epsilon$. In particular, if the columns of $A$ are normalized to be unit length, our total variation distance guarantee implies a bound on the sum of the $\ell_2$ distances between the column vectors of $A$ and $A'$, $\sum_{i =1}^d \|a_i-\hat{a}_i\|_2 = O(\epsilon)$. In contrast, the strongest known prior results only yield a $\epsilon^{O(1)}$ (relative) bound on the distance between individual $a_i$'s and their estimates and translate into an $O(d\epsilon)$ bound on the total variation distance. Our key innovation is a new approach to ICA (even to outlier-free ICA) that circumvents the difficulties in the classical method of moments and instead relies on a new geometric certificate of correctness of an affine transformation. Our algorithm is based on a new method that iteratively improves an estimate of the unknown affine transformation whenever the requirements of the certificate are not met.

Galaxy Spin Classification I: Z-wise vs S-wise Spirals With Chirality Equivariant Residual Network

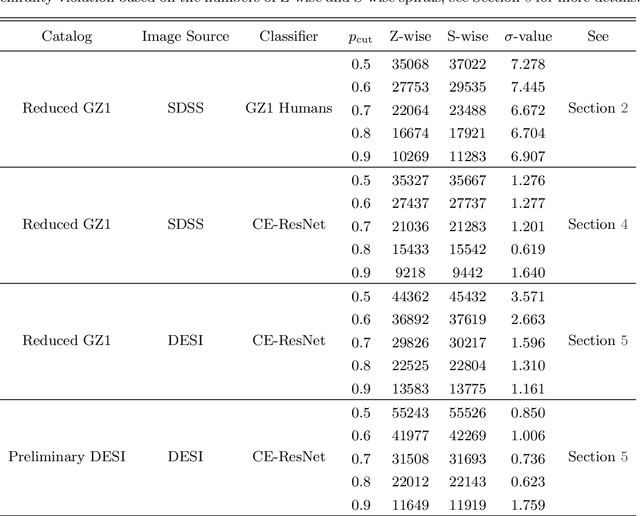
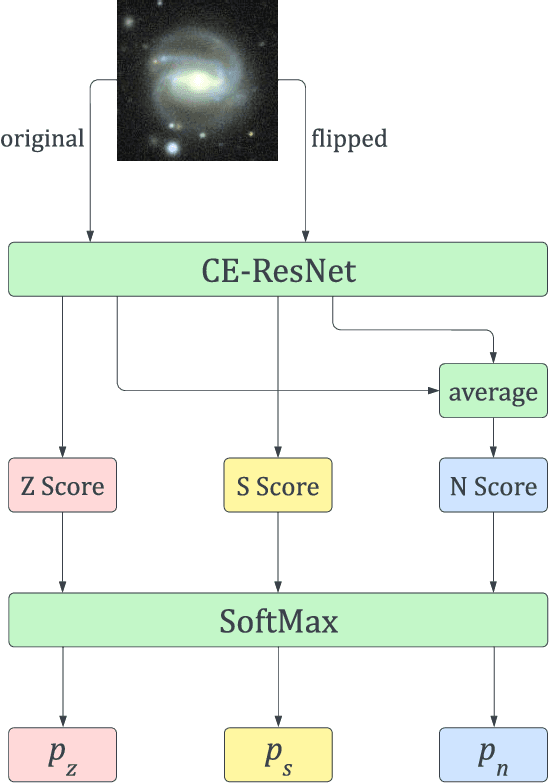
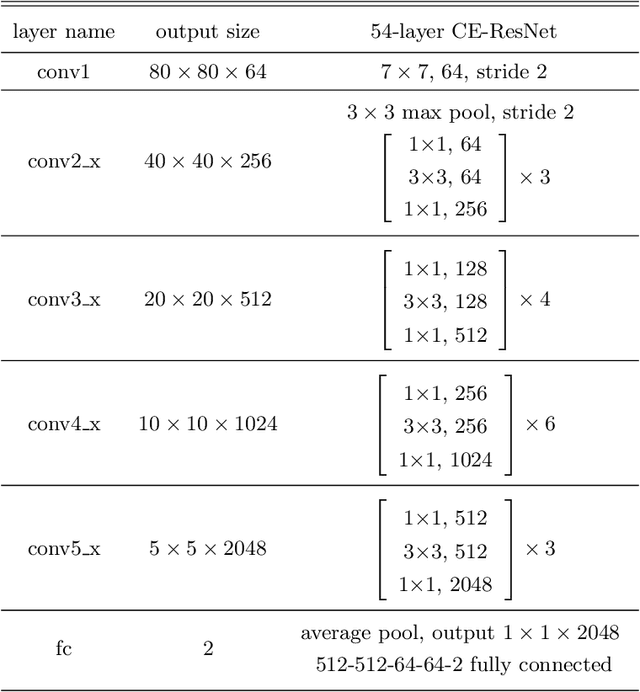
The angular momentum of galaxies (galaxy spin) contains rich information about the initial condition of the Universe, yet it is challenging to efficiently measure the spin direction for the tremendous amount of galaxies that are being mapped by the ongoing and forthcoming cosmological surveys. We present a machine learning based classifier for the Z-wise vs S-wise spirals, which can help to break the degeneracy in the galaxy spin direction measurement. The proposed Chirality Equivariant Residual Network (CE-ResNet) is manifestly equivariant under a reflection of the input image, which guarantees that there is no inherent asymmetry between the Z-wise and S-wise probability estimators. We train the model with Sloan Digital Sky Survey (SDSS) images, with the training labels given by the Galaxy Zoo 1 (GZ1) project. A combination of data augmentation tricks are used during the training, making the model more robust to be applied to other surveys. We find a $\sim\!30\%$ increase of both types of spirals when Dark Energy Spectroscopic Instrument (DESI) images are used for classification, due to the better imaging quality of DESI. We verify that the $\sim\!7\sigma$ difference between the numbers of Z-wise and S-wise spirals is due to human bias, since the discrepancy drops to $<\!1.8\sigma$ with our CE-ResNet classification results. We discuss the potential systematics that are relevant to the future cosmological applications.

Robustly Learning Mixtures of $k$ Arbitrary Gaussians

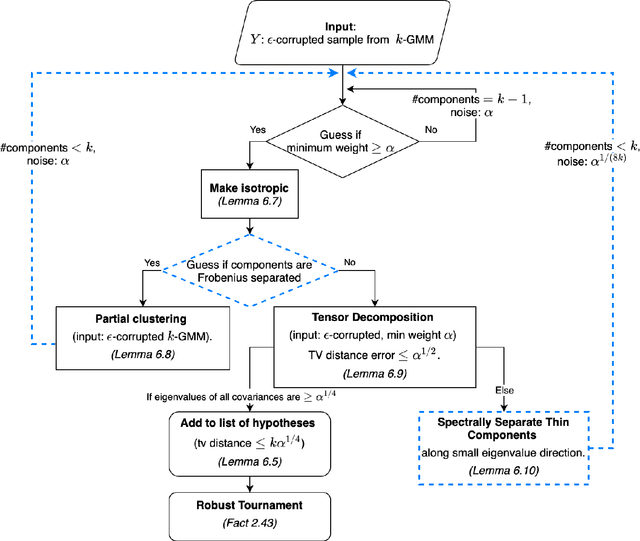
We give a polynomial-time algorithm for the problem of robustly estimating a mixture of $k$ arbitrary Gaussians in $\mathbb{R}^d$, for any fixed $k$, in the presence of a constant fraction of arbitrary corruptions. This resolves the main open problem in several previous works on algorithmic robust statistics, which addressed the special cases of robustly estimating (a) a single Gaussian, (b) a mixture of TV-distance separated Gaussians, and (c) a uniform mixture of two Gaussians. Our main tools are an efficient \emph{partial clustering} algorithm that relies on the sum-of-squares method, and a novel tensor decomposition algorithm that allows errors in both Frobenius norm and low-rank terms.

Normalizing Constant Estimation with Gaussianized Bridge Sampling

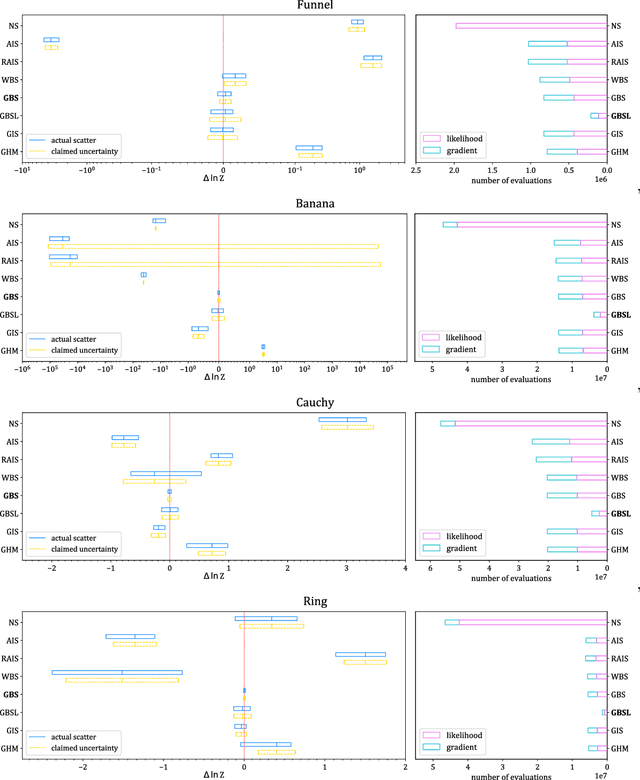
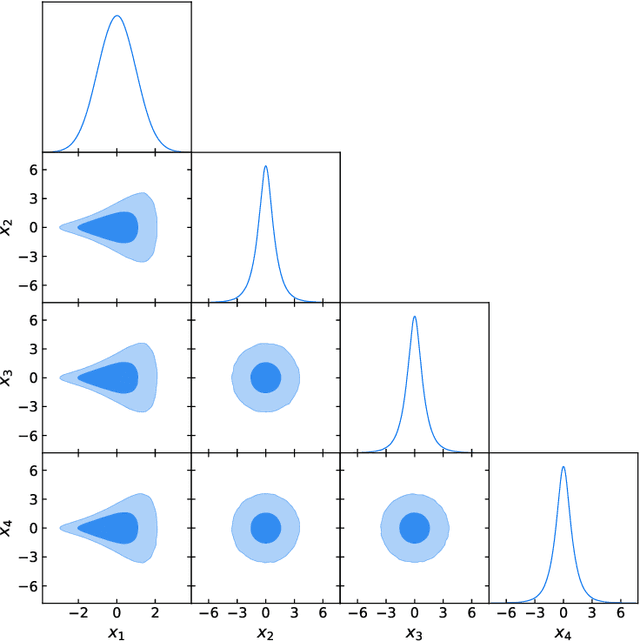
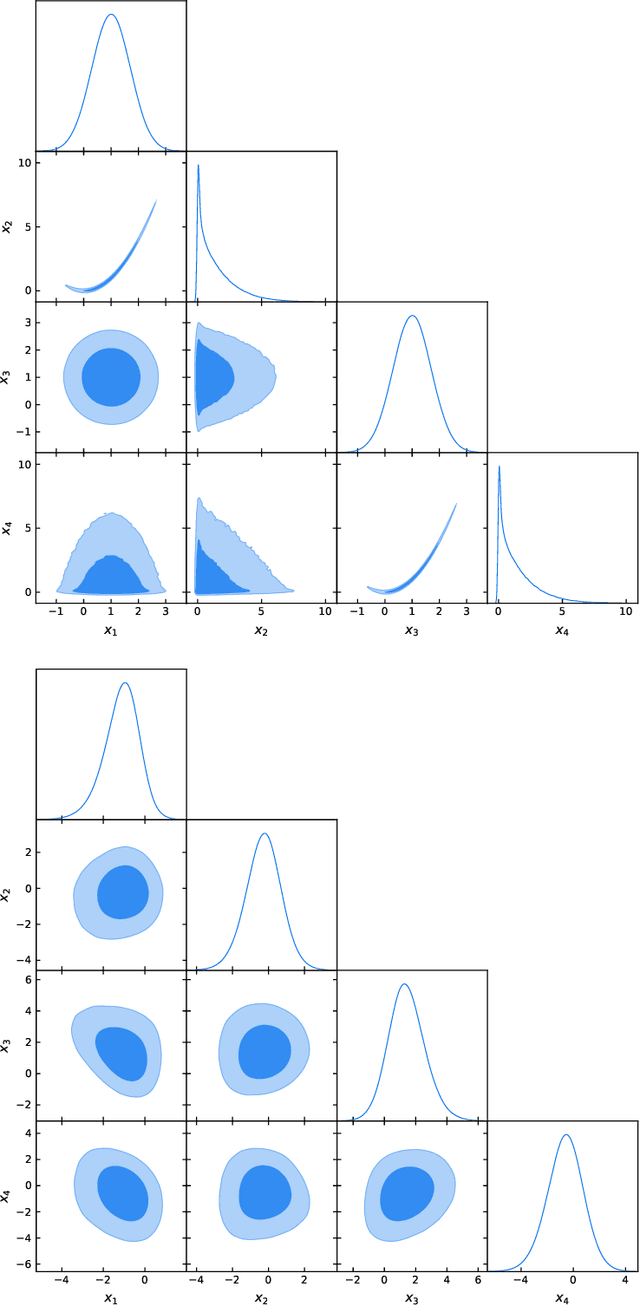
Normalizing constant (also called partition function, Bayesian evidence, or marginal likelihood) is one of the central goals of Bayesian inference, yet most of the existing methods are both expensive and inaccurate. Here we develop a new approach, starting from posterior samples obtained with a standard Markov Chain Monte Carlo (MCMC). We apply a novel Normalizing Flow (NF) approach to obtain an analytic density estimator from these samples, followed by Optimal Bridge Sampling (OBS) to obtain the normalizing constant. We compare our method which we call Gaussianized Bridge Sampling (GBS) to existing methods such as Nested Sampling (NS) and Annealed Importance Sampling (AIS) on several examples, showing our method is both significantly faster and substantially more accurate than these methods, and comes with a reliable error estimation.

Robustly Clustering a Mixture of Gaussians

We give an efficient algorithm for robustly clustering of a mixture of arbitrary Gaussians, a central open problem in the theory of computationally efficient robust estimation, assuming only that for each pair of component Gaussians, their means are well-separated or their covariances are well-separated.