Robustly Learning Mixtures of $k$ Arbitrary Gaussians
Paper and Code
Dec 31, 2020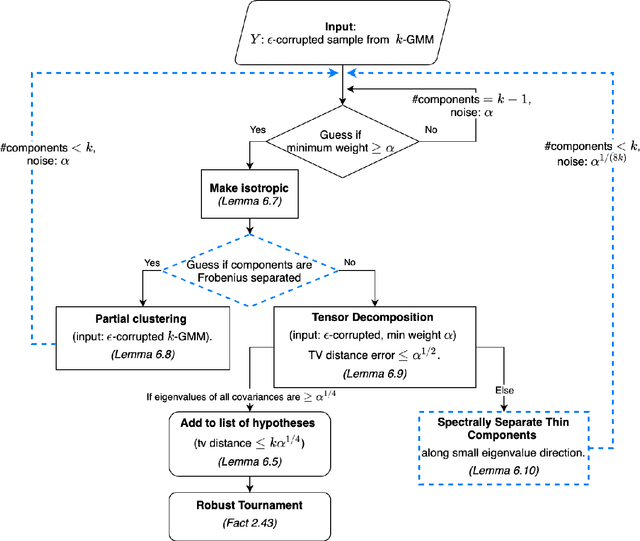
We give a polynomial-time algorithm for the problem of robustly estimating a mixture of $k$ arbitrary Gaussians in $\mathbb{R}^d$, for any fixed $k$, in the presence of a constant fraction of arbitrary corruptions. This resolves the main open problem in several previous works on algorithmic robust statistics, which addressed the special cases of robustly estimating (a) a single Gaussian, (b) a mixture of TV-distance separated Gaussians, and (c) a uniform mixture of two Gaussians. Our main tools are an efficient \emph{partial clustering} algorithm that relies on the sum-of-squares method, and a novel tensor decomposition algorithm that allows errors in both Frobenius norm and low-rank terms.
* This version fixes an issue with a technical statement (Fact 2.35 in
the previous arXiv version, replaced by Lemmas 2.38 and 2.41 in the current
version) that claimed a bound on the variance of a more general class of
distributions than what is needed in our approach
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge