Persistent Sampling: Unleashing the Potential of Sequential Monte Carlo

Sequential Monte Carlo (SMC) methods are powerful tools for Bayesian inference but suffer from requiring many particles for accurate estimates, leading to high computational costs. We introduce persistent sampling (PS), an extension of SMC that mitigates this issue by allowing particles from previous iterations to persist. This generates a growing, weighted ensemble of particles distributed across iterations. In each iteration, PS utilizes multiple importance sampling and resampling from the mixture of all previous distributions to produce the next generation of particles. This addresses particle impoverishment and mode collapse, resulting in more accurate posterior approximations. Furthermore, this approach provides lower-variance marginal likelihood estimates for model comparison. Additionally, the persistent particles improve transition kernel adaptation for efficient exploration. Experiments on complex distributions show that PS consistently outperforms standard methods, achieving lower squared bias in posterior moment estimation and significantly reduced marginal likelihood errors, all at a lower computational cost. PS offers a robust, efficient, and scalable framework for Bayesian inference.

Sequential Kalman Monte Carlo for gradient-free inference in Bayesian inverse problems

Ensemble Kalman Inversion (EKI) has been proposed as an efficient method for solving inverse problems with expensive forward models. However, the method is based on the assumption that we proceed through a sequence of Gaussian measures in moving from the prior to the posterior, and that the forward model is linear. In this work, we introduce Sequential Kalman Monte Carlo (SKMC) samplers, where we exploit EKI and Flow Annealed Kalman Inversion (FAKI) within a Sequential Monte Carlo (SMC) sampling scheme to perform efficient gradient-free inference in Bayesian inverse problems. FAKI employs normalizing flows (NF) to relax the Gaussian ansatz of the target measures in EKI. NFs are able to learn invertible maps between a Gaussian latent space and the original data space, allowing us to perform EKI updates in the Gaussianized NF latent space. However, FAKI alone is not able to correct for the model linearity assumptions in EKI. Errors in the particle distribution as we move through the sequence of target measures can therefore compound to give incorrect posterior moment estimates. In this work we consider the use of EKI and FAKI to initialize the particle distribution for each target in an adaptive SMC annealing scheme, before performing t-preconditioned Crank-Nicolson (tpCN) updates to distribute particles according to the target. We demonstrate the performance of these SKMC samplers on three challenging numerical benchmarks, showing significant improvements in the rate of convergence compared to standard SMC with importance weighted resampling at each temperature level. Code implementing the SKMC samplers is available at https://github.com/RichardGrumitt/KalmanMC.

Flow Annealed Kalman Inversion for Gradient-Free Inference in Bayesian Inverse Problems

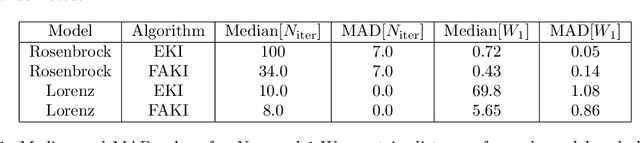
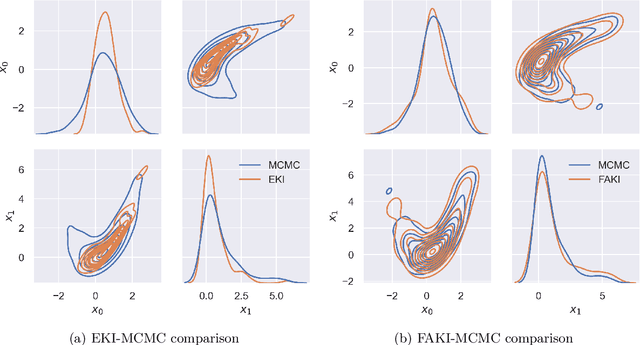
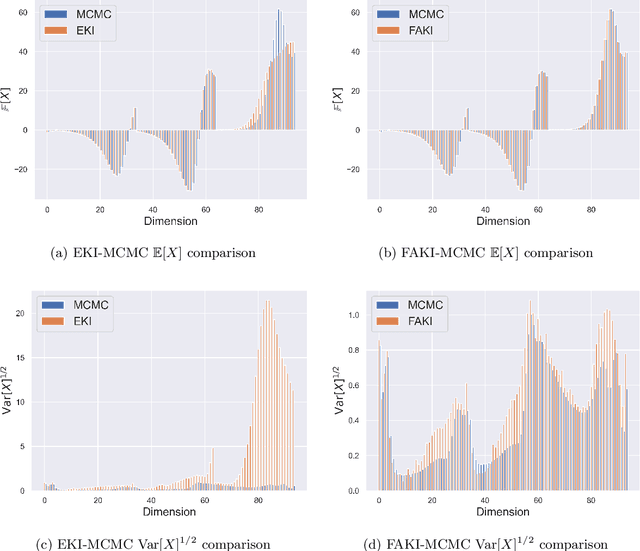
For many scientific inverse problems we are required to evaluate an expensive forward model. Moreover, the model is often given in such a form that it is unrealistic to access its gradients. In such a scenario, standard Markov Chain Monte Carlo algorithms quickly become impractical, requiring a large number of serial model evaluations to converge on the target distribution. In this paper we introduce Flow Annealed Kalman Inversion (FAKI). This is a generalization of Ensemble Kalman Inversion (EKI), where we embed the Kalman filter updates in a temperature annealing scheme, and use normalizing flows (NF) to map the intermediate measures corresponding to each temperature level to the standard Gaussian. In doing so, we relax the Gaussian ansatz for the intermediate measures used in standard EKI, allowing us to achieve higher fidelity approximations to non-Gaussian targets. We demonstrate the performance of FAKI on two numerical benchmarks, showing dramatic improvements over standard EKI in terms of accuracy whilst accelerating its already rapid convergence properties (typically in $\mathcal{O}(10)$ steps).

Ensemble Slice Sampling

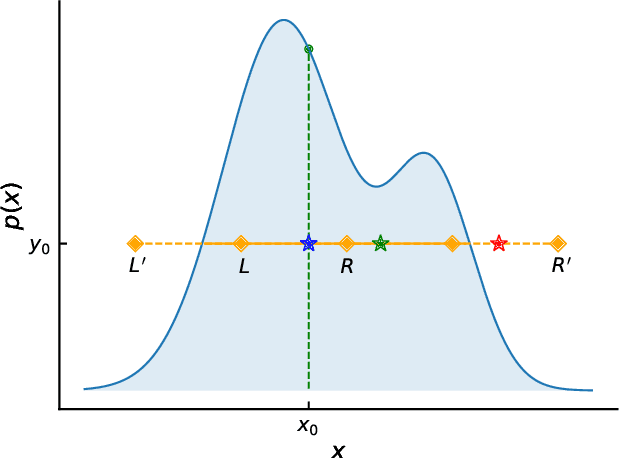
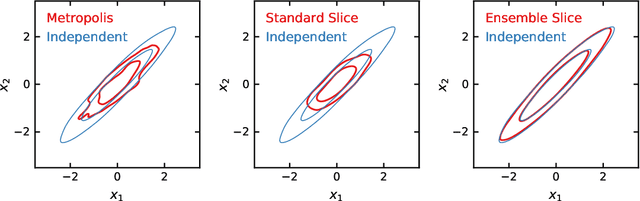
Slice Sampling has emerged as a powerful Markov Chain Monte Carlo algorithm that adapts to the characteristics of the target distribution with minimal hand-tuning. However, Slice Sampling's performance is highly sensitive to the user-specified initial length scale hyperparameter. Moreover, Slice Sampling generally struggles with poorly scaled or strongly correlated distributions. This paper introduces Ensemble Slice Sampling, a new class of algorithms that bypasses such difficulties by adaptively tuning the length scale. Furthermore, Ensemble Slice Sampling's performance is immune to linear correlations by exploiting an ensemble of parallel walkers. These algorithms are trivial to construct, require no hand-tuning, and can easily be implemented in parallel computing environments. Empirical tests show that Ensemble Slice Sampling can improve efficiency by more than an order of magnitude compared to conventional MCMC methods on highly correlated target distributions such as the Autoregressive Process of Order 1 and the Correlated Funnel distribution.