Local primordial non-Gaussianity from the large-scale clustering of photometric DESI luminous red galaxies

We use angular clustering of luminous red galaxies from the Dark Energy Spectroscopic Instrument (DESI) imaging surveys to constrain the local primordial non-Gaussianity parameter fNL. Our sample comprises over 12 million targets, covering 14,000 square degrees of the sky, with redshifts in the range 0.2< z < 1.35. We identify Galactic extinction, survey depth, and astronomical seeing as the primary sources of systematic error, and employ linear regression and artificial neural networks to alleviate non-cosmological excess clustering on large scales. Our methods are tested against log-normal simulations with and without fNL and systematics, showing superior performance of the neural network treatment in reducing remaining systematics. Assuming the universality relation, we find fNL $= 47^{+14(+29)}_{-11(-22)}$ at 68\%(95\%) confidence. With a more aggressive treatment, including regression against the full set of imaging maps, our maximum likelihood value shifts slightly to fNL$ \sim 50$ and the uncertainty on fNL increases due to the removal of large-scale clustering information. We apply a series of robustness tests (e.g., cuts on imaging, declination, or scales used) that show consistency in the obtained constraints. Despite extensive efforts to mitigate systematics, our measurements indicate fNL > 0 with a 99.9 percent confidence level. This outcome raises concerns as it could be attributed to unforeseen systematics, including calibration errors or uncertainties associated with low-\ell systematics in the extinction template. Alternatively, it could suggest a scale-dependent fNL model--causing significant non-Gaussianity around large-scale structure while leaving cosmic microwave background scales unaffected. Our results encourage further studies of fNL with DESI spectroscopic samples, where the inclusion of 3D clustering modes should help separate imaging systematics.

Ensemble Slice Sampling

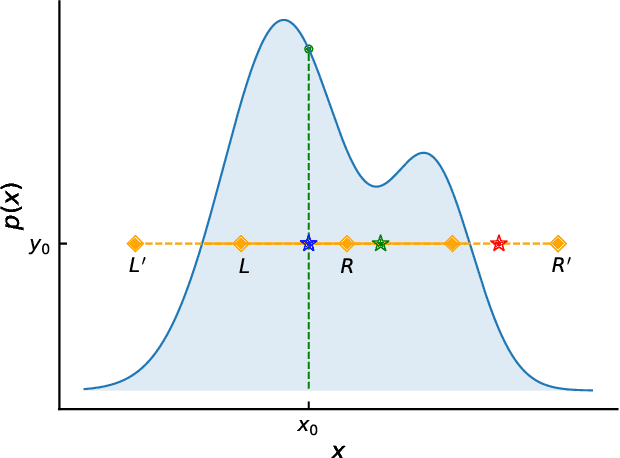
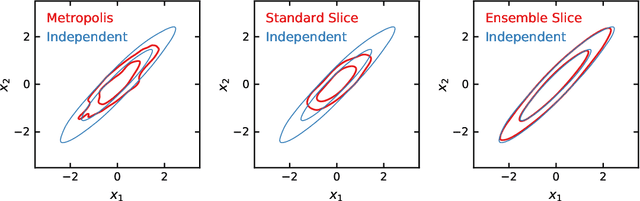
Slice Sampling has emerged as a powerful Markov Chain Monte Carlo algorithm that adapts to the characteristics of the target distribution with minimal hand-tuning. However, Slice Sampling's performance is highly sensitive to the user-specified initial length scale hyperparameter. Moreover, Slice Sampling generally struggles with poorly scaled or strongly correlated distributions. This paper introduces Ensemble Slice Sampling, a new class of algorithms that bypasses such difficulties by adaptively tuning the length scale. Furthermore, Ensemble Slice Sampling's performance is immune to linear correlations by exploiting an ensemble of parallel walkers. These algorithms are trivial to construct, require no hand-tuning, and can easily be implemented in parallel computing environments. Empirical tests show that Ensemble Slice Sampling can improve efficiency by more than an order of magnitude compared to conventional MCMC methods on highly correlated target distributions such as the Autoregressive Process of Order 1 and the Correlated Funnel distribution.