Ensemble Slice Sampling

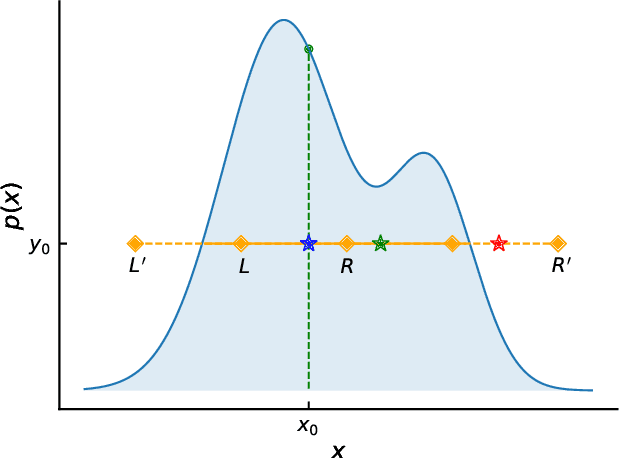
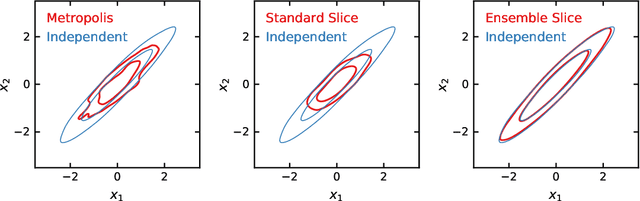
Slice Sampling has emerged as a powerful Markov Chain Monte Carlo algorithm that adapts to the characteristics of the target distribution with minimal hand-tuning. However, Slice Sampling's performance is highly sensitive to the user-specified initial length scale hyperparameter. Moreover, Slice Sampling generally struggles with poorly scaled or strongly correlated distributions. This paper introduces Ensemble Slice Sampling, a new class of algorithms that bypasses such difficulties by adaptively tuning the length scale. Furthermore, Ensemble Slice Sampling's performance is immune to linear correlations by exploiting an ensemble of parallel walkers. These algorithms are trivial to construct, require no hand-tuning, and can easily be implemented in parallel computing environments. Empirical tests show that Ensemble Slice Sampling can improve efficiency by more than an order of magnitude compared to conventional MCMC methods on highly correlated target distributions such as the Autoregressive Process of Order 1 and the Correlated Funnel distribution.