Opportunities in AI/ML for the Rubin LSST Dark Energy Science Collaboration

The Vera C. Rubin Observatory's Legacy Survey of Space and Time (LSST) will produce unprecedented volumes of heterogeneous astronomical data (images, catalogs, and alerts) that challenge traditional analysis pipelines. The LSST Dark Energy Science Collaboration (DESC) aims to derive robust constraints on dark energy and dark matter from these data, requiring methods that are statistically powerful, scalable, and operationally reliable. Artificial intelligence and machine learning (AI/ML) are already embedded across DESC science workflows, from photometric redshifts and transient classification to weak lensing inference and cosmological simulations. Yet their utility for precision cosmology hinges on trustworthy uncertainty quantification, robustness to covariate shift and model misspecification, and reproducible integration within scientific pipelines. This white paper surveys the current landscape of AI/ML across DESC's primary cosmological probes and cross-cutting analyses, revealing that the same core methodologies and fundamental challenges recur across disparate science cases. Since progress on these cross-cutting challenges would benefit multiple probes simultaneously, we identify key methodological research priorities, including Bayesian inference at scale, physics-informed methods, validation frameworks, and active learning for discovery. With an eye on emerging techniques, we also explore the potential of the latest foundation model methodologies and LLM-driven agentic AI systems to reshape DESC workflows, provided their deployment is coupled with rigorous evaluation and governance. Finally, we discuss critical software, computing, data infrastructure, and human capital requirements for the successful deployment of these new methodologies, and consider associated risks and opportunities for broader coordination with external actors.

Hybrid Physical-Neural Simulator for Fast Cosmological Hydrodynamics

Cosmological field-level inference requires differentiable forward models that solve the challenging dynamics of gas and dark matter under hydrodynamics and gravity. We propose a hybrid approach where gravitational forces are computed using a differentiable particle-mesh solver, while the hydrodynamics are parametrized by a neural network that maps local quantities to an effective pressure field. We demonstrate that our method improves upon alternative approaches, such as an Enthalpy Gradient Descent baseline, both at the field and summary-statistic level. The approach is furthermore highly data efficient, with a single reference simulation of cosmological structure formation being sufficient to constrain the neural pressure model. This opens the door for future applications where the model is fit directly to observational data, rather than a training set of simulations.

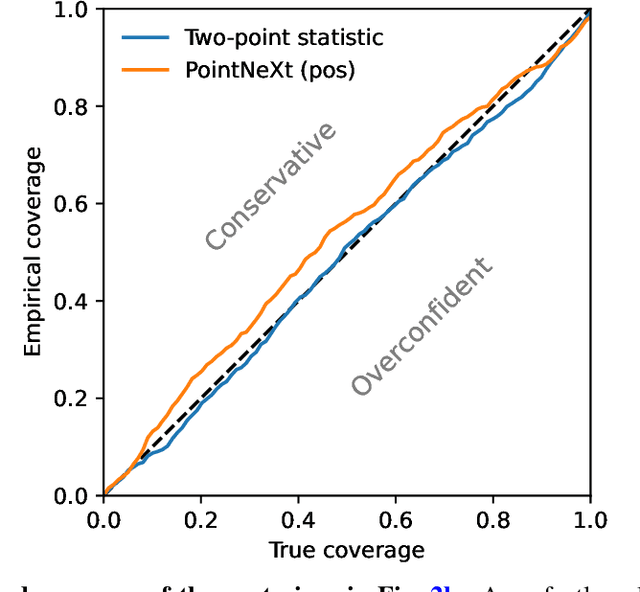
Cosmology from Galaxy Redshift Surveys with PointNet

In recent years, deep learning approaches have achieved state-of-the-art results in the analysis of point cloud data. In cosmology, galaxy redshift surveys resemble such a permutation invariant collection of positions in space. These surveys have so far mostly been analysed with two-point statistics, such as power spectra and correlation functions. The usage of these summary statistics is best justified on large scales, where the density field is linear and Gaussian. However, in light of the increased precision expected from upcoming surveys, the analysis of -- intrinsically non-Gaussian -- small angular separations represents an appealing avenue to better constrain cosmological parameters. In this work, we aim to improve upon two-point statistics by employing a \textit{PointNet}-like neural network to regress the values of the cosmological parameters directly from point cloud data. Our implementation of PointNets can analyse inputs of $\mathcal{O}(10^4) - \mathcal{O}(10^5)$ galaxies at a time, which improves upon earlier work for this application by roughly two orders of magnitude. Additionally, we demonstrate the ability to analyse galaxy redshift survey data on the lightcone, as opposed to previously static simulation boxes at a given fixed redshift.

Painting with baryons: augmenting N-body simulations with gas using deep generative models

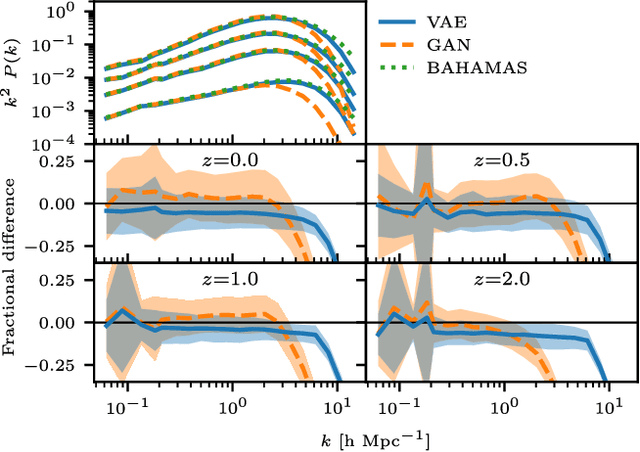
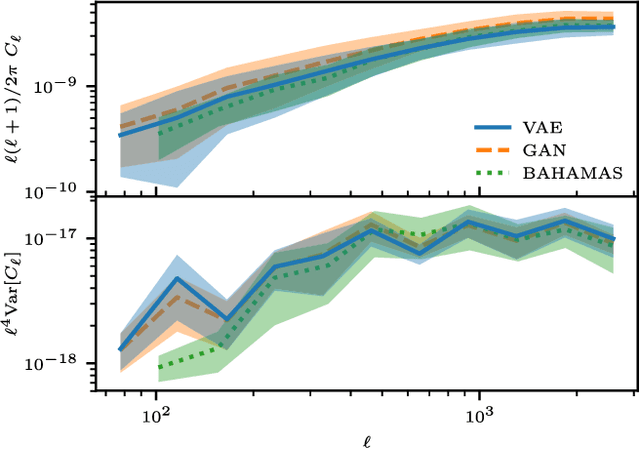
Running hydrodynamical simulations to produce mock data of large-scale structure and baryonic probes, such as the thermal Sunyaev-Zeldovich (tSZ) effect, at cosmological scales is computationally challenging. We propose to leverage the expressive power of deep generative models to find an effective description of the large-scale gas distribution and temperature. We train two deep generative models, a variational auto-encoder and a generative adversarial network, on pairs of matter density and pressure slices from the BAHAMAS hydrodynamical simulation. The trained models are able to successfully map matter density to the corresponding gas pressure. We then apply the trained models on 100 lines-of-sight from SLICS, a suite of N-body simulations optimised for weak lensing covariance estimation, to generate maps of the tSZ effect. The generated tSZ maps are found to be statistically consistent with those from BAHAMAS. We conclude by considering a specific observable, the angular cross-power spectrum between the weak lensing convergence and the tSZ effect and its variance, where we find excellent agreement between the predictions from BAHAMAS and SLICS, thus enabling the use of SLICS for tSZ covariance estimation.