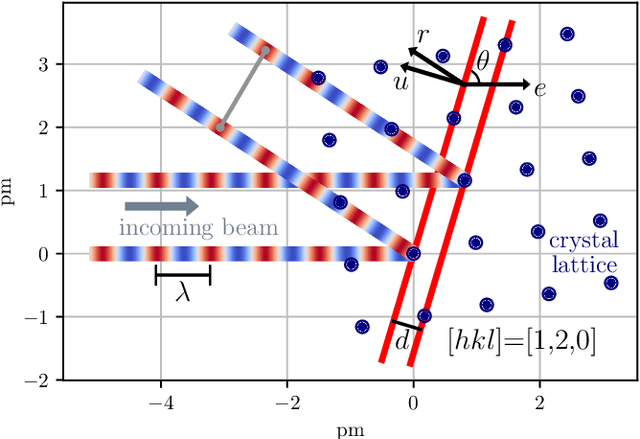
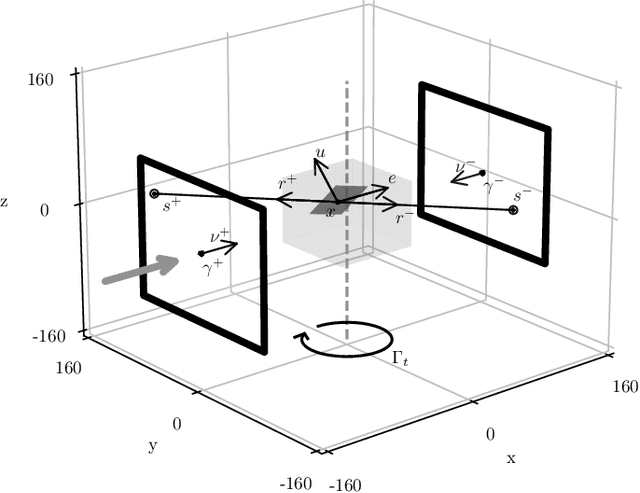
Laue Indexing with Optimal Transport

Laue tomography experiments retrieve the positions and orientations of crystal grains in a polycrystalline samples from diffraction patterns recorded at multiple viewing angles. The use of a broad wavelength spectrum beam can greatly reduce the experimental time, but poses a difficult challenge for the indexing of diffraction peaks in polycrystalline samples; the information about the wavelength of these Bragg peaks is absent and the diffraction patterns from multiple grains are superimposed. To date, no algorithms exist capable of indexing samples with more than about 500 grains efficiently. To address this need we present a novel method: Laue indexing with Optimal Transport (LaueOT). We create a probabilistic description of the multi-grain indexing problem and propose a solution based on Sinkhorn Expectation-Maximization method, which allows to efficiently find the maximum of the likelihood thanks to the assignments being calculated using Optimal Transport. This is a non-convex optimization problem, where the orientations and positions of grains are optimized simultaneously with grain-to-spot assignments, while robustly handling the outliers. The selection of initial prototype grains to consider in the optimization problem are also calculated within the Optimal Transport framework. LaueOT can rapidly and effectively index up to 1000 grains on a single large memory GPU within less than 30 minutes. We demonstrate the performance of LaueOT on simulations with variable numbers of grains, spot position measurement noise levels, and outlier fractions. The algorithm recovers the correct number of grains even for high noise levels and up to 70% outliers in our experiments. We compare the results of indexing with LaueOT to existing algorithms both on synthetic and real neutron diffraction data from well-characterized samples.

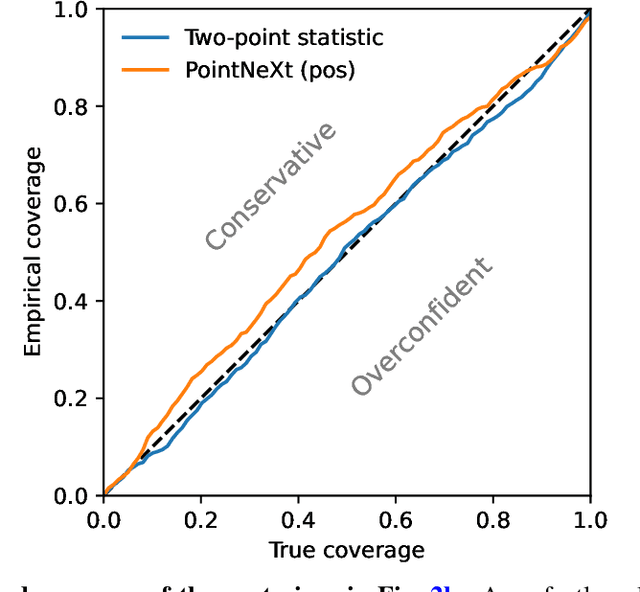
Cosmology from Galaxy Redshift Surveys with PointNet

In recent years, deep learning approaches have achieved state-of-the-art results in the analysis of point cloud data. In cosmology, galaxy redshift surveys resemble such a permutation invariant collection of positions in space. These surveys have so far mostly been analysed with two-point statistics, such as power spectra and correlation functions. The usage of these summary statistics is best justified on large scales, where the density field is linear and Gaussian. However, in light of the increased precision expected from upcoming surveys, the analysis of -- intrinsically non-Gaussian -- small angular separations represents an appealing avenue to better constrain cosmological parameters. In this work, we aim to improve upon two-point statistics by employing a \textit{PointNet}-like neural network to regress the values of the cosmological parameters directly from point cloud data. Our implementation of PointNets can analyse inputs of $\mathcal{O}(10^4) - \mathcal{O}(10^5)$ galaxies at a time, which improves upon earlier work for this application by roughly two orders of magnitude. Additionally, we demonstrate the ability to analyse galaxy redshift survey data on the lightcone, as opposed to previously static simulation boxes at a given fixed redshift.

DeepLSS: breaking parameter degeneracies in large scale structure with deep learning analysis of combined probes

In classical cosmological analysis of large scale structure surveys with 2-pt functions, the parameter measurement precision is limited by several key degeneracies within the cosmology and astrophysics sectors. For cosmic shear, clustering amplitude $\sigma_8$ and matter density $\Omega_m$ roughly follow the $S_8=\sigma_8(\Omega_m/0.3)^{0.5}$ relation. In turn, $S_8$ is highly correlated with the intrinsic galaxy alignment amplitude $A_{\rm{IA}}$. For galaxy clustering, the bias $b_g$ is degenerate with both $\sigma_8$ and $\Omega_m$, as well as the stochasticity $r_g$. Moreover, the redshift evolution of IA and bias can cause further parameter confusion. A tomographic 2-pt probe combination can partially lift these degeneracies. In this work we demonstrate that a deep learning analysis of combined probes of weak gravitational lensing and galaxy clustering, which we call DeepLSS, can effectively break these degeneracies and yield significantly more precise constraints on $\sigma_8$, $\Omega_m$, $A_{\rm{IA}}$, $b_g$, $r_g$, and IA redshift evolution parameter $\eta_{\rm{IA}}$. The most significant gains are in the IA sector: the precision of $A_{\rm{IA}}$ is increased by approximately 8x and is almost perfectly decorrelated from $S_8$. Galaxy bias $b_g$ is improved by 1.5x, stochasticity $r_g$ by 3x, and the redshift evolution $\eta_{\rm{IA}}$ and $\eta_b$ by 1.6x. Breaking these degeneracies leads to a significant gain in constraining power for $\sigma_8$ and $\Omega_m$, with the figure of merit improved by 15x. We give an intuitive explanation for the origin of this information gain using sensitivity maps. These results indicate that the fully numerical, map-based forward modeling approach to cosmological inference with machine learning may play an important role in upcoming LSS surveys. We discuss perspectives and challenges in its practical deployment for a full survey analysis.

Emulation of cosmological mass maps with conditional generative adversarial networks

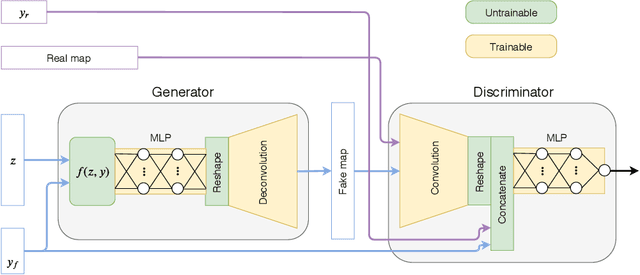
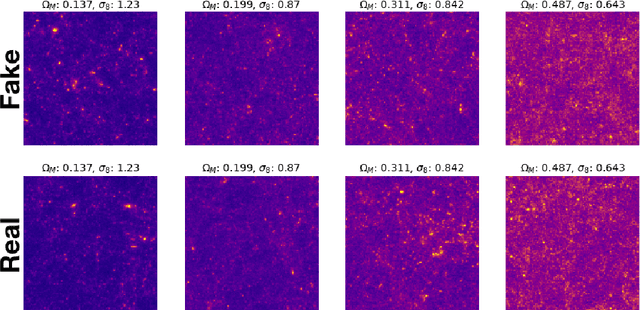
Mass maps created using weak gravitational lensing techniques play a crucial role in understanding the evolution of structures in the universe and our ability to constrain cosmological models. The mass maps are based on computationally expensive N-body simulations, which can create a computational bottleneck for data analysis. Simulation-based emulators of observables are starting to play an increasingly important role in cosmology, as the analytical predictions are expected to reach their precision limits for upcoming experiments. Modern deep generative models, such as Generative Adversarial Networks (GANs), have demonstrated their potential to significantly reduce the computational cost of generating such simulations and generate the observable mass maps directly. Until now, most GAN approaches produce simulations for a fixed value of the cosmological parameters, which limits their practical applicability. We instead propose a new conditional model that is able to generate simulations for arbitrary cosmological parameters spanned by the space of simulations. Our results show that unseen cosmologies can be generated with high statistical accuracy and visual quality. This contribution is a step towards emulating weak lensing observables at the map level, as opposed to the summary statistic level.

Cosmological N-body simulations: a challenge for scalable generative models

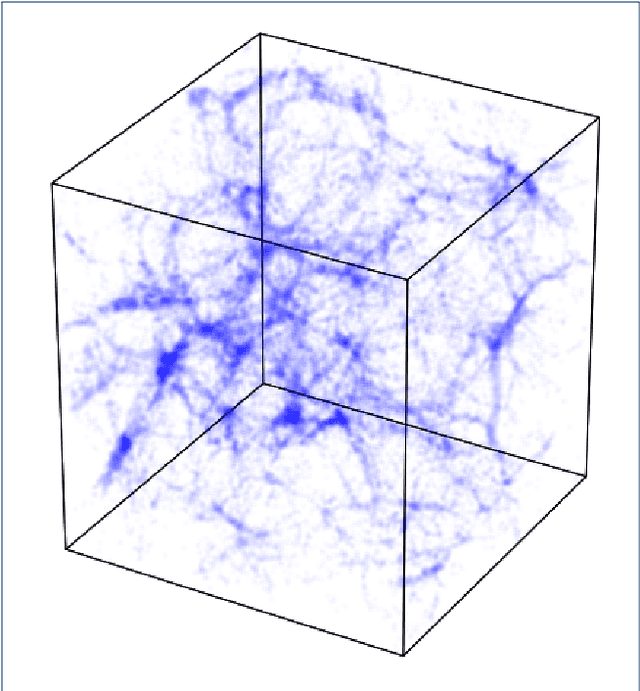
Deep generative models, such as Generative Adversarial Networks (GANs) or Variational Autoencoders have been demonstrated to produce images of high visual quality. However, the existing hardware on which these models are trained severely limits the size of the images that can be generated. The rapid growth of high dimensional data in many fields of science therefore poses a significant challenge for generative models. In cosmology, the large-scale, 3D matter distribution, modeled with N-body simulations, plays a crucial role in understanding of evolution of structures in the universe. As these simulations are computationally very expensive, GANs have recently generated interest as a possible method to emulate these datasets, but they have been, so far, mostly limited to 2D data. In this work, we introduce a new benchmark for the generation of 3D N-body simulations, in order to stimulate new ideas in the machine learning community and move closer to the practical use of generative models in cosmology. As a first benchmark result, we propose a scalable GAN approach for training a generator of N-body 3D cubes. Our technique relies on two key building blocks, (i) splitting the generation of the high-dimensional data into smaller parts, and (ii) using a multi-scale approach that efficiently captures global image features that might otherwise be lost in the splitting process. We evaluate the performance of our model for the generation of N-body samples using various statistical measures commonly used in cosmology. Our results show that the proposed model produces samples of high visual quality, although the statistical analysis reveals that capturing rare features in the data poses significant problems for the generative models. We make the data, quality evaluation routines, and the proposed GAN architecture publicly available at https://github.com/nperraud/3DcosmoGAN

DeepSphere: towards an equivariant graph-based spherical CNN

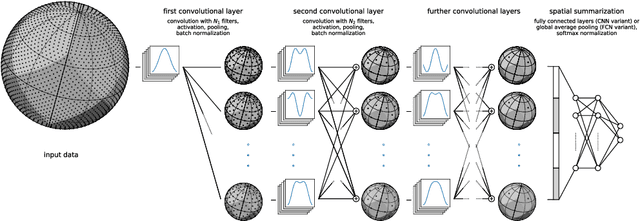
Spherical data is found in many applications. By modeling the discretized sphere as a graph, we can accommodate non-uniformly distributed, partial, and changing samplings. Moreover, graph convolutions are computationally more efficient than spherical convolutions. As equivariance is desired to exploit rotational symmetries, we discuss how to approach rotation equivariance using the graph neural network introduced in Defferrard et al. (2016). Experiments show good performance on rotation-invariant learning problems. Code and examples are available at https://github.com/SwissDataScienceCenter/DeepSphere

DeepSphere: Efficient spherical Convolutional Neural Network with HEALPix sampling for cosmological applications

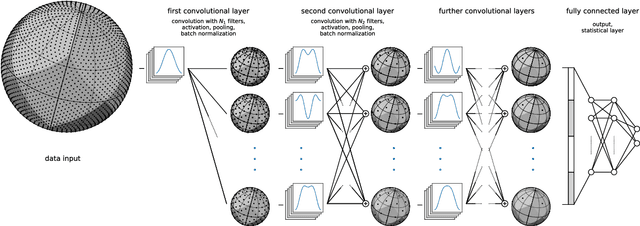
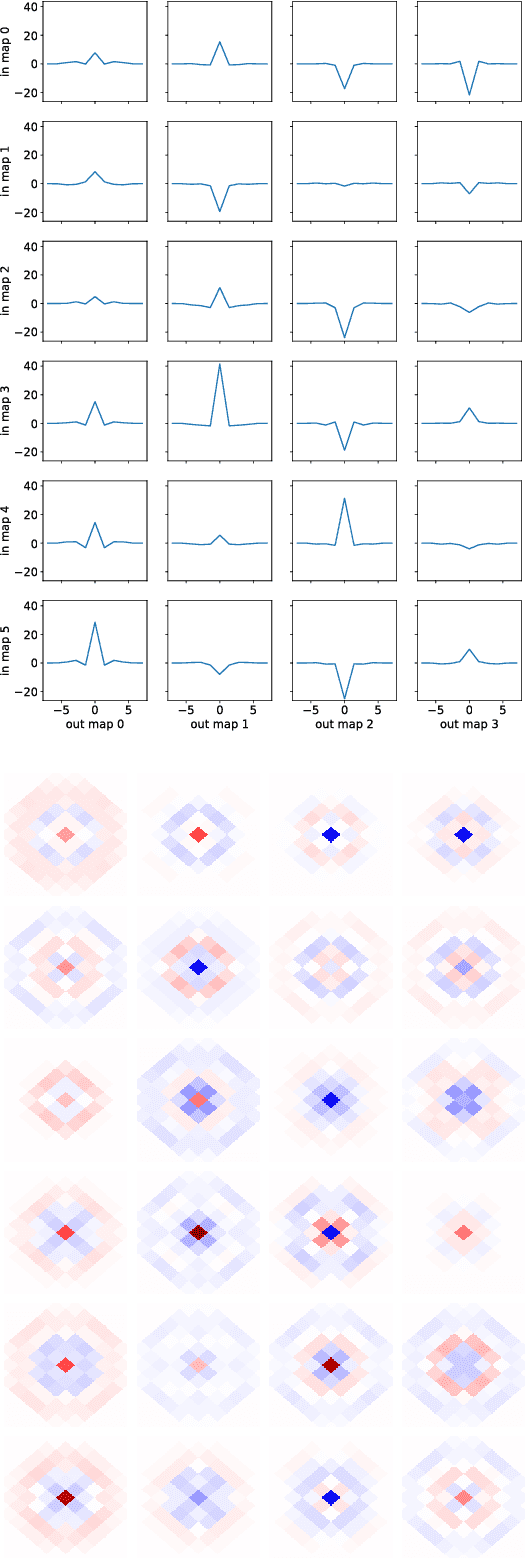
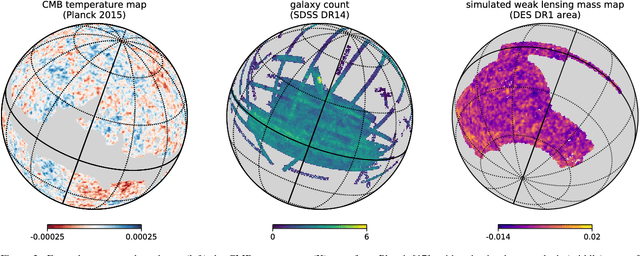
Convolutional Neural Networks (CNNs) are a cornerstone of the Deep Learning toolbox and have led to many breakthroughs in Artificial Intelligence. These networks have mostly been developed for regular Euclidean domains such as those supporting images, audio, or video. Because of their success, CNN-based methods are becoming increasingly popular in Cosmology. Cosmological data often comes as spherical maps, which make the use of the traditional CNNs more complicated. The commonly used pixelization scheme for spherical maps is the Hierarchical Equal Area isoLatitude Pixelisation (HEALPix). We present a spherical CNN for analysis of full and partial HEALPix maps, which we call DeepSphere. The spherical CNN is constructed by representing the sphere as a graph. Graphs are versatile data structures that can act as a discrete representation of a continuous manifold. Using the graph-based representation, we define many of the standard CNN operations, such as convolution and pooling. With filters restricted to being radial, our convolutions are equivariant to rotation on the sphere, and DeepSphere can be made invariant or equivariant to rotation. This way, DeepSphere is a special case of a graph CNN, tailored to the HEALPix sampling of the sphere. This approach is computationally more efficient than using spherical harmonics to perform convolutions. We demonstrate the method on a classification problem of weak lensing mass maps from two cosmological models and compare the performance of the CNN with that of two baseline classifiers. The results show that the performance of DeepSphere is always superior or equal to both of these baselines. For high noise levels and for data covering only a smaller fraction of the sphere, DeepSphere achieves typically 10% better classification accuracy than those baselines. Finally, we show how learned filters can be visualized to introspect the neural network.

Fast Cosmic Web Simulations with Generative Adversarial Networks

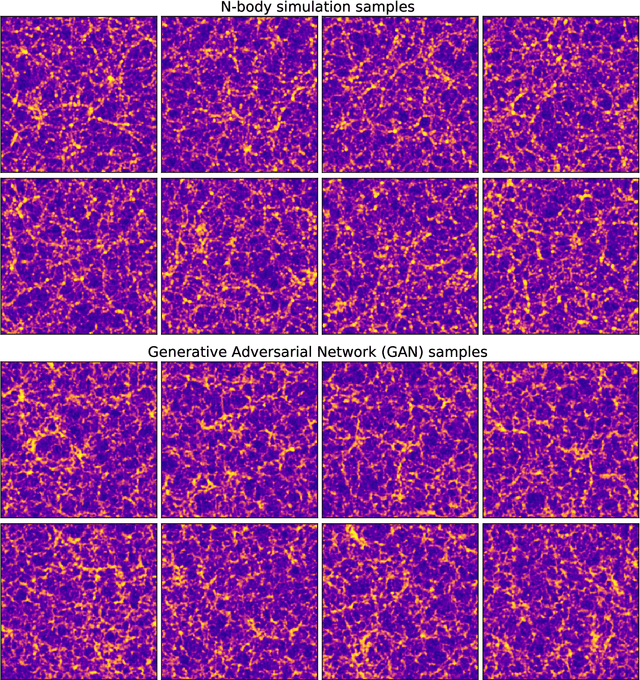
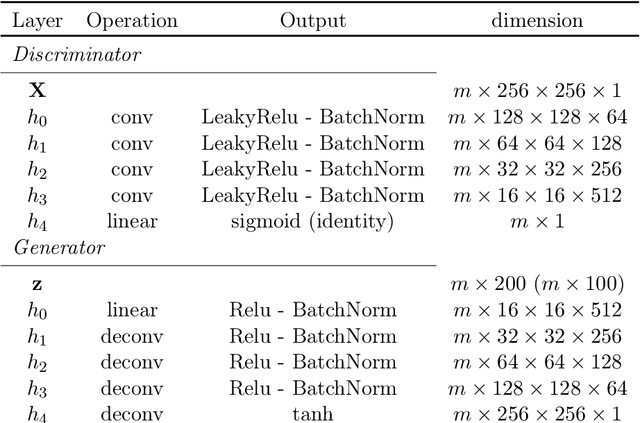
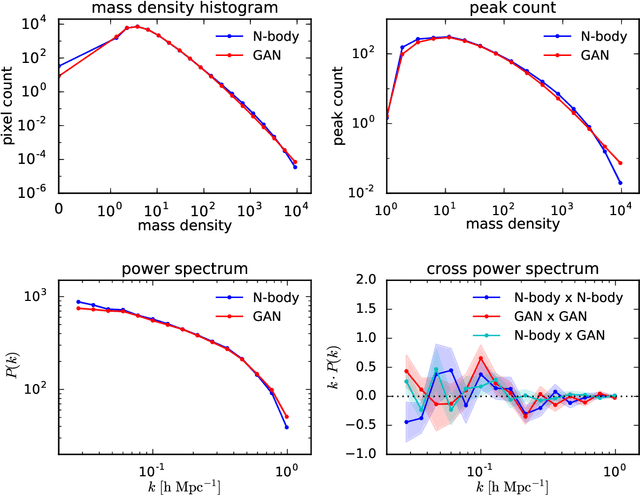
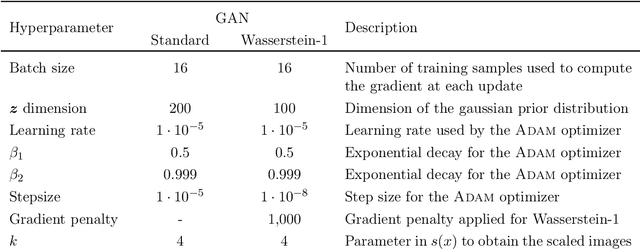
Dark matter in the universe evolves through gravity to form a complex network of halos, filaments, sheets and voids, that is known as the cosmic web. Computational models of the underlying physical processes, such as classical N-body simulations, are extremely resource intensive, as they track the action of gravity in an expanding universe using billions of particles as tracers of the cosmic matter distribution. Therefore, upcoming cosmology experiments will face a computational bottleneck that may limit the exploitation of their full scientific potential. To address this challenge, we demonstrate the application of a machine learning technique called Generative Adversarial Networks (GAN) to learn models that can efficiently generate new, physically realistic realizations of the cosmic web. Our training set is a small, representative sample of 2D image snapshots from N-body simulations of size 500 and 100 Mpc. We show that the GAN-produced results are qualitatively and quantitatively very similar to the originals. Generation of a new cosmic web realization with a GAN takes a fraction of a second, compared to the many hours needed by the N-body technique. We anticipate that GANs will therefore play an important role in providing extremely fast and precise simulations of cosmic web in the era of large cosmological surveys, such as Euclid and LSST.

Fast Point Spread Function Modeling with Deep Learning

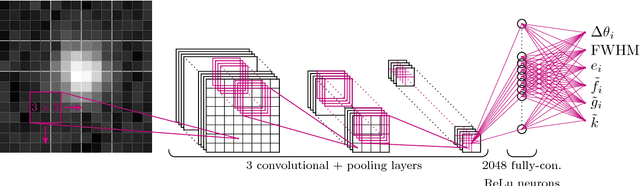
Modeling the Point Spread Function (PSF) of wide-field surveys is vital for many astrophysical applications and cosmological probes including weak gravitational lensing. The PSF smears the image of any recorded object and therefore needs to be taken into account when inferring properties of galaxies from astronomical images. In the case of cosmic shear, the PSF is one of the dominant sources of systematic errors and must be treated carefully to avoid biases in cosmological parameters. Recently, forward modeling approaches to calibrate shear measurements within the Monte-Carlo Control Loops ($MCCL$) framework have been developed. These methods typically require simulating a large amount of wide-field images, thus, the simulations need to be very fast yet have realistic properties in key features such as the PSF pattern. Hence, such forward modeling approaches require a very flexible PSF model, which is quick to evaluate and whose parameters can be estimated reliably from survey data. We present a PSF model that meets these requirements based on a fast deep-learning method to estimate its free parameters. We demonstrate our approach on publicly available SDSS data. We extract the most important features of the SDSS sample via principal component analysis. Next, we construct our model based on perturbations of a fixed base profile, ensuring that it captures these features. We then train a Convolutional Neural Network to estimate the free parameters of the model from noisy images of the PSF. This allows us to render a model image of each star, which we compare to the SDSS stars to evaluate the performance of our method. We find that our approach is able to accurately reproduce the SDSS PSF at the pixel level, which, due to the speed of both the model evaluation and the parameter estimation, offers good prospects for incorporating our method into the $MCCL$ framework.

Accelerating Approximate Bayesian Computation with Quantile Regression: Application to Cosmological Redshift Distributions

Approximate Bayesian Computation (ABC) is a method to obtain a posterior distribution without a likelihood function, using simulations and a set of distance metrics. For that reason, it has recently been gaining popularity as an analysis tool in cosmology and astrophysics. Its drawback, however, is a slow convergence rate. We propose a novel method, which we call qABC, to accelerate ABC with Quantile Regression. In this method, we create a model of quantiles of distance measure as a function of input parameters. This model is trained on a small number of simulations and estimates which regions of the prior space are likely to be accepted into the posterior. Other regions are then immediately rejected. This procedure is then repeated as more simulations are available. We apply it to the practical problem of estimation of redshift distribution of cosmological samples, using forward modelling developed in previous work. The qABC method converges to nearly same posterior as the basic ABC. It uses, however, only 20\% of the number of simulations compared to basic ABC, achieving a fivefold gain in execution time for our problem. For other problems the acceleration rate may vary; it depends on how close the prior is to the final posterior. We discuss possible improvements and extensions to this method.