Ankit Srivastava
Generative AI in Live Operations: Evidence of Productivity Gains in Cybersecurity and Endpoint Management
Apr 09, 2025



Abstract:We measure the association between generative AI (GAI) tool adoption and four metrics spanning security operations, information protection, and endpoint management: 1) number of security alerts per incident, 2) probability of security incident reopenings, 3) time to classify a data loss prevention alert, and 4) time to resolve device policy conflicts. We find that GAI is associated with robust and statistically and practically significant improvements in the four metrics. Although unobserved confounders inhibit causal identification, these results are among the first to use observational data from live operations to investigate the relationship between GAI adoption and security operations, data loss prevention, and device policy management.
Using R-functions to Control the Shape of Soft Robots
Jun 05, 2023Abstract:In this paper, we introduce a new approach for soft robot shape formation and morphing using approximate distance fields. The method uses concepts from constructive solid geometry, R-functions, to construct an approximate distance function to the boundary of a domain in $\Re^d$. The gradients of the R-functions can then be used to generate control algorithms for shape formation tasks for soft robots. By construction, R-functions are smooth and convex everywhere, possess precise differential properties, and easily extend from $\Re^2$ to $\Re^3$ if needed. Furthermore, R-function theory provides a straightforward method to creating composite distance functions for any desired shape by combining subsets of distance functions. The process is highly efficient since the shape description is an analytical expression, and in this sense, it is better than competing control algorithms such as those based on potential fields. Although the method could also apply to swarm robots, in this paper it is applied to soft robots to demonstrate shape formation and morphing in 2-D (simulation and experimentation) and 3-D (simulation).
Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks
Apr 17, 2021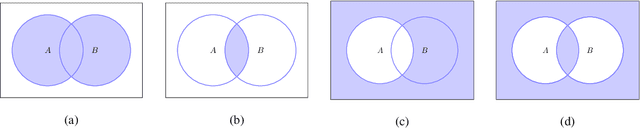

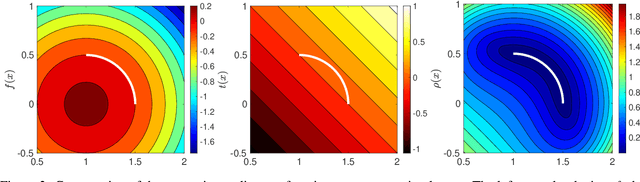
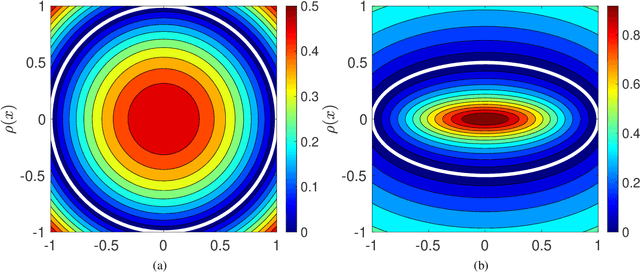
Abstract:In this paper, we introduce a new approach based on distance fields to exactly impose boundary conditions in physics-informed deep neural networks. The challenges in satisfying Dirichlet boundary conditions in meshfree and particle methods are well-known. This issue is also pertinent in the development of physics informed neural networks (PINN) for the solution of partial differential equations. We introduce geometry-aware trial functions in artifical neural networks to improve the training in deep learning for partial differential equations. To this end, we use concepts from constructive solid geometry (R-functions) and generalized barycentric coordinates (mean value potential fields) to construct $\phi$, an approximate distance function to the boundary of a domain. To exactly impose homogeneous Dirichlet boundary conditions, the trial function is taken as $\phi$ multiplied by the PINN approximation, and its generalization via transfinite interpolation is used to a priori satisfy inhomogeneous Dirichlet (essential), Neumann (natural), and Robin boundary conditions on complex geometries. In doing so, we eliminate modeling error associated with the satisfaction of boundary conditions in a collocation method and ensure that kinematic admissibility is met pointwise in a Ritz method. We present numerical solutions for linear and nonlinear boundary-value problems over domains with affine and curved boundaries. Benchmark problems in 1D for linear elasticity, advection-diffusion, and beam bending; and in 2D for the Poisson equation, biharmonic equation, and the nonlinear Eikonal equation are considered. The approach extends to higher dimensions, and we showcase its use by solving a Poisson problem with homogeneneous Dirichlet boundary conditions over the 4D hypercube. This study provides a pathway for meshfree analysis to be conducted on the exact geometry without domain discretization.
Cosmological N-body simulations: a challenge for scalable generative models
Aug 15, 2019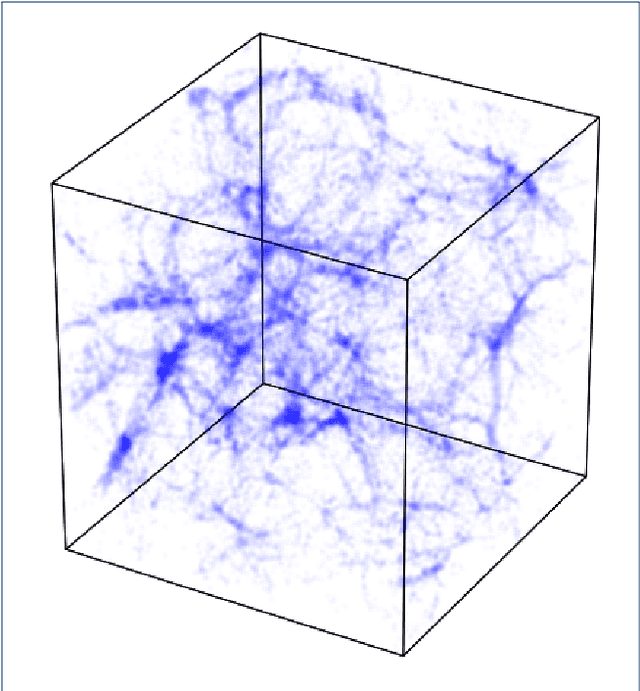



Abstract:Deep generative models, such as Generative Adversarial Networks (GANs) or Variational Autoencoders have been demonstrated to produce images of high visual quality. However, the existing hardware on which these models are trained severely limits the size of the images that can be generated. The rapid growth of high dimensional data in many fields of science therefore poses a significant challenge for generative models. In cosmology, the large-scale, 3D matter distribution, modeled with N-body simulations, plays a crucial role in understanding of evolution of structures in the universe. As these simulations are computationally very expensive, GANs have recently generated interest as a possible method to emulate these datasets, but they have been, so far, mostly limited to 2D data. In this work, we introduce a new benchmark for the generation of 3D N-body simulations, in order to stimulate new ideas in the machine learning community and move closer to the practical use of generative models in cosmology. As a first benchmark result, we propose a scalable GAN approach for training a generator of N-body 3D cubes. Our technique relies on two key building blocks, (i) splitting the generation of the high-dimensional data into smaller parts, and (ii) using a multi-scale approach that efficiently captures global image features that might otherwise be lost in the splitting process. We evaluate the performance of our model for the generation of N-body samples using various statistical measures commonly used in cosmology. Our results show that the proposed model produces samples of high visual quality, although the statistical analysis reveals that capturing rare features in the data poses significant problems for the generative models. We make the data, quality evaluation routines, and the proposed GAN architecture publicly available at https://github.com/nperraud/3DcosmoGAN
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge