Fast Cosmic Web Simulations with Generative Adversarial Networks

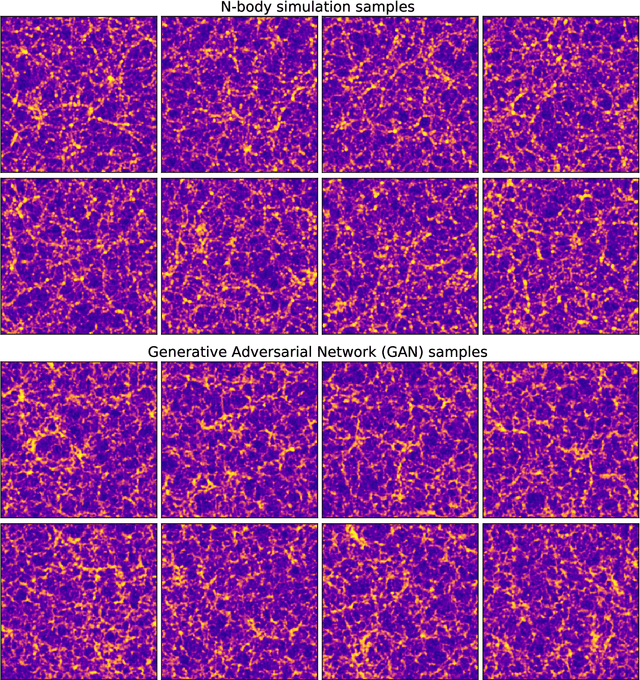
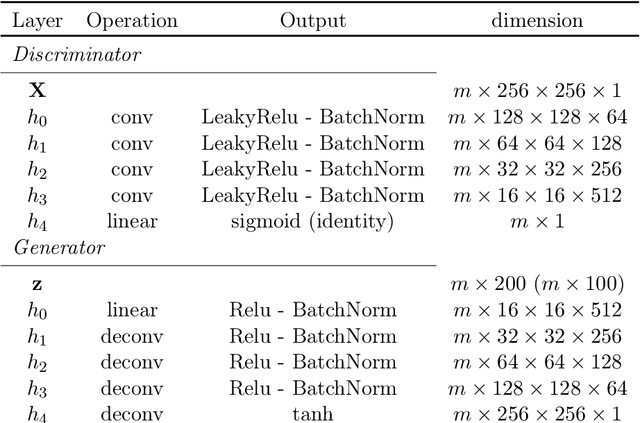
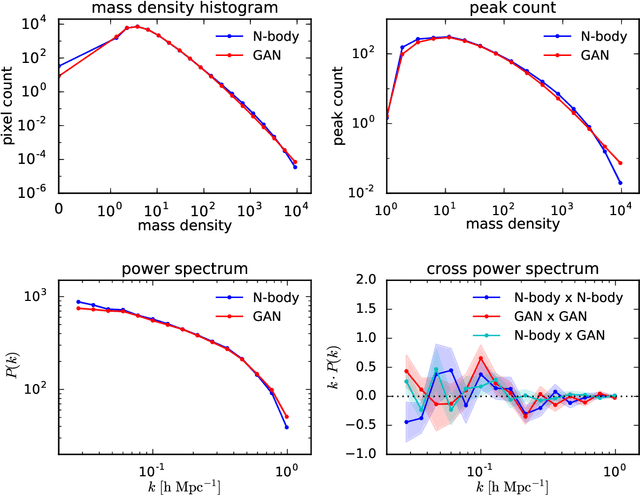
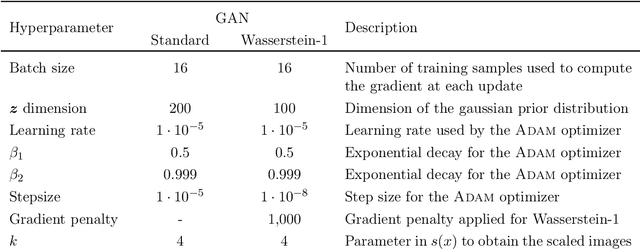
Dark matter in the universe evolves through gravity to form a complex network of halos, filaments, sheets and voids, that is known as the cosmic web. Computational models of the underlying physical processes, such as classical N-body simulations, are extremely resource intensive, as they track the action of gravity in an expanding universe using billions of particles as tracers of the cosmic matter distribution. Therefore, upcoming cosmology experiments will face a computational bottleneck that may limit the exploitation of their full scientific potential. To address this challenge, we demonstrate the application of a machine learning technique called Generative Adversarial Networks (GAN) to learn models that can efficiently generate new, physically realistic realizations of the cosmic web. Our training set is a small, representative sample of 2D image snapshots from N-body simulations of size 500 and 100 Mpc. We show that the GAN-produced results are qualitatively and quantitatively very similar to the originals. Generation of a new cosmic web realization with a GAN takes a fraction of a second, compared to the many hours needed by the N-body technique. We anticipate that GANs will therefore play an important role in providing extremely fast and precise simulations of cosmic web in the era of large cosmological surveys, such as Euclid and LSST.

Fast Point Spread Function Modeling with Deep Learning

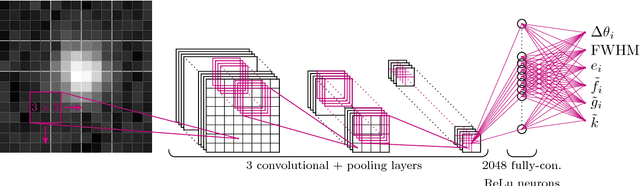
Modeling the Point Spread Function (PSF) of wide-field surveys is vital for many astrophysical applications and cosmological probes including weak gravitational lensing. The PSF smears the image of any recorded object and therefore needs to be taken into account when inferring properties of galaxies from astronomical images. In the case of cosmic shear, the PSF is one of the dominant sources of systematic errors and must be treated carefully to avoid biases in cosmological parameters. Recently, forward modeling approaches to calibrate shear measurements within the Monte-Carlo Control Loops ($MCCL$) framework have been developed. These methods typically require simulating a large amount of wide-field images, thus, the simulations need to be very fast yet have realistic properties in key features such as the PSF pattern. Hence, such forward modeling approaches require a very flexible PSF model, which is quick to evaluate and whose parameters can be estimated reliably from survey data. We present a PSF model that meets these requirements based on a fast deep-learning method to estimate its free parameters. We demonstrate our approach on publicly available SDSS data. We extract the most important features of the SDSS sample via principal component analysis. Next, we construct our model based on perturbations of a fixed base profile, ensuring that it captures these features. We then train a Convolutional Neural Network to estimate the free parameters of the model from noisy images of the PSF. This allows us to render a model image of each star, which we compare to the SDSS stars to evaluate the performance of our method. We find that our approach is able to accurately reproduce the SDSS PSF at the pixel level, which, due to the speed of both the model evaluation and the parameter estimation, offers good prospects for incorporating our method into the $MCCL$ framework.

Accelerating Approximate Bayesian Computation with Quantile Regression: Application to Cosmological Redshift Distributions

Approximate Bayesian Computation (ABC) is a method to obtain a posterior distribution without a likelihood function, using simulations and a set of distance metrics. For that reason, it has recently been gaining popularity as an analysis tool in cosmology and astrophysics. Its drawback, however, is a slow convergence rate. We propose a novel method, which we call qABC, to accelerate ABC with Quantile Regression. In this method, we create a model of quantiles of distance measure as a function of input parameters. This model is trained on a small number of simulations and estimates which regions of the prior space are likely to be accepted into the posterior. Other regions are then immediately rejected. This procedure is then repeated as more simulations are available. We apply it to the practical problem of estimation of redshift distribution of cosmological samples, using forward modelling developed in previous work. The qABC method converges to nearly same posterior as the basic ABC. It uses, however, only 20\% of the number of simulations compared to basic ABC, achieving a fivefold gain in execution time for our problem. For other problems the acceleration rate may vary; it depends on how close the prior is to the final posterior. We discuss possible improvements and extensions to this method.

Cosmological model discrimination with Deep Learning

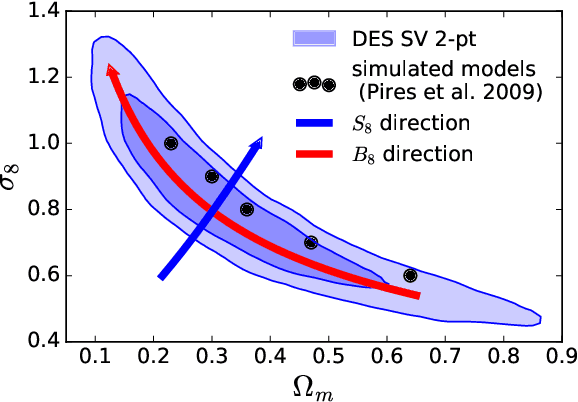
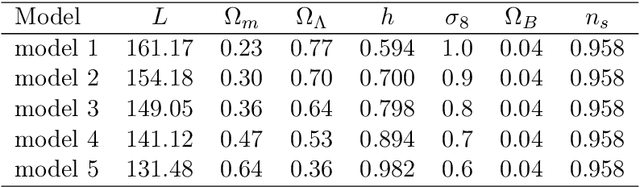
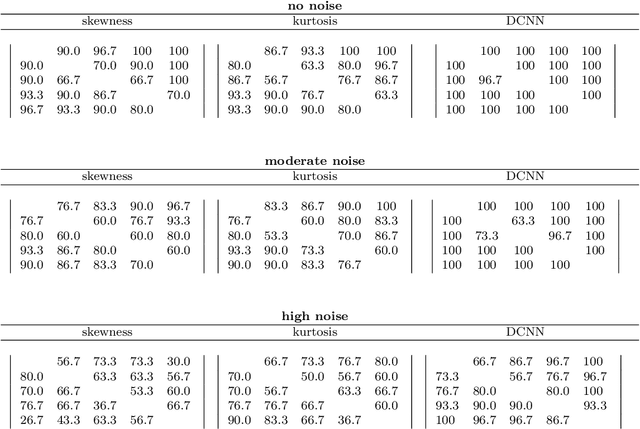
We demonstrate the potential of Deep Learning methods for measurements of cosmological parameters from density fields, focusing on the extraction of non-Gaussian information. We consider weak lensing mass maps as our dataset. We aim for our method to be able to distinguish between five models, which were chosen to lie along the $\sigma_8$ - $\Omega_m$ degeneracy, and have nearly the same two-point statistics. We design and implement a Deep Convolutional Neural Network (DCNN) which learns the relation between five cosmological models and the mass maps they generate. We develop a new training strategy which ensures the good performance of the network for high levels of noise. We compare the performance of this approach to commonly used non-Gaussian statistics, namely the skewness and kurtosis of the convergence maps. We find that our implementation of DCNN outperforms the skewness and kurtosis statistics, especially for high noise levels. The network maintains the mean discrimination efficiency greater than $85\%$ even for noise levels corresponding to ground based lensing observations, while the other statistics perform worse in this setting, achieving efficiency less than $70\%$. This demonstrates the ability of CNN-based methods to efficiently break the $\sigma_8$ - $\Omega_m$ degeneracy with weak lensing mass maps alone. We discuss the potential of this method to be applied to the analysis of real weak lensing data and other datasets.