Raphael Sgier
DeepSphere: towards an equivariant graph-based spherical CNN
Apr 08, 2019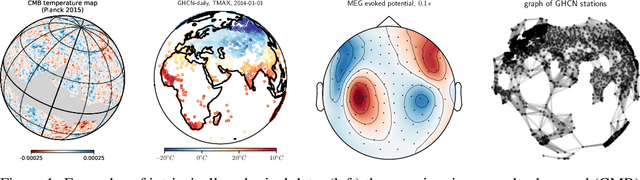


Abstract:Spherical data is found in many applications. By modeling the discretized sphere as a graph, we can accommodate non-uniformly distributed, partial, and changing samplings. Moreover, graph convolutions are computationally more efficient than spherical convolutions. As equivariance is desired to exploit rotational symmetries, we discuss how to approach rotation equivariance using the graph neural network introduced in Defferrard et al. (2016). Experiments show good performance on rotation-invariant learning problems. Code and examples are available at https://github.com/SwissDataScienceCenter/DeepSphere
DeepSphere: Efficient spherical Convolutional Neural Network with HEALPix sampling for cosmological applications
Oct 29, 2018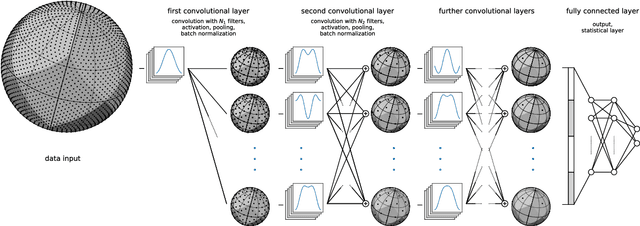

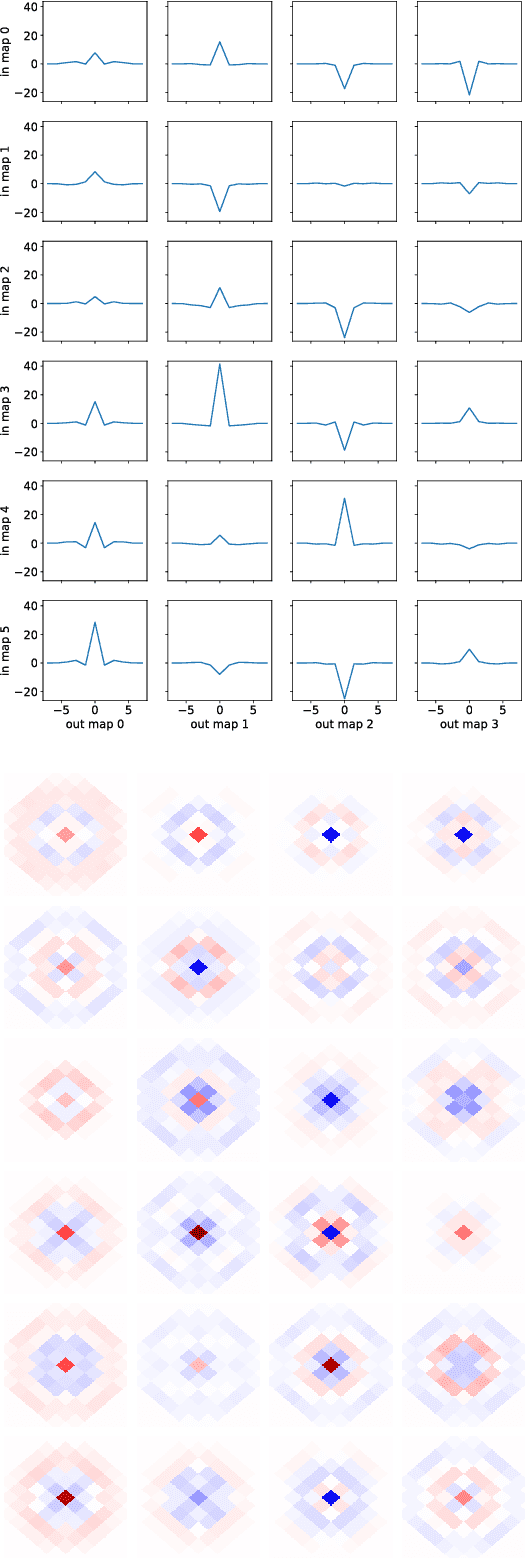
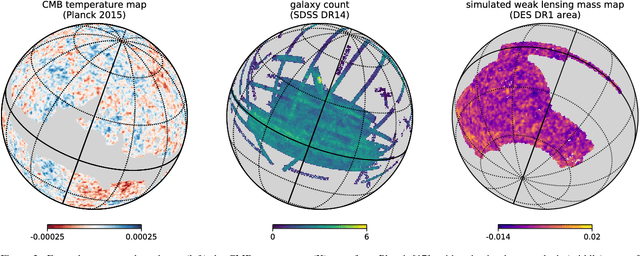
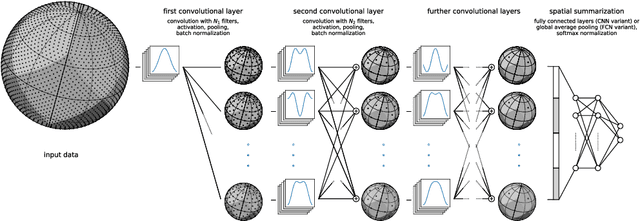
Abstract:Convolutional Neural Networks (CNNs) are a cornerstone of the Deep Learning toolbox and have led to many breakthroughs in Artificial Intelligence. These networks have mostly been developed for regular Euclidean domains such as those supporting images, audio, or video. Because of their success, CNN-based methods are becoming increasingly popular in Cosmology. Cosmological data often comes as spherical maps, which make the use of the traditional CNNs more complicated. The commonly used pixelization scheme for spherical maps is the Hierarchical Equal Area isoLatitude Pixelisation (HEALPix). We present a spherical CNN for analysis of full and partial HEALPix maps, which we call DeepSphere. The spherical CNN is constructed by representing the sphere as a graph. Graphs are versatile data structures that can act as a discrete representation of a continuous manifold. Using the graph-based representation, we define many of the standard CNN operations, such as convolution and pooling. With filters restricted to being radial, our convolutions are equivariant to rotation on the sphere, and DeepSphere can be made invariant or equivariant to rotation. This way, DeepSphere is a special case of a graph CNN, tailored to the HEALPix sampling of the sphere. This approach is computationally more efficient than using spherical harmonics to perform convolutions. We demonstrate the method on a classification problem of weak lensing mass maps from two cosmological models and compare the performance of the CNN with that of two baseline classifiers. The results show that the performance of DeepSphere is always superior or equal to both of these baselines. For high noise levels and for data covering only a smaller fraction of the sphere, DeepSphere achieves typically 10% better classification accuracy than those baselines. Finally, we show how learned filters can be visualized to introspect the neural network.
Fast Cosmic Web Simulations with Generative Adversarial Networks
Sep 20, 2018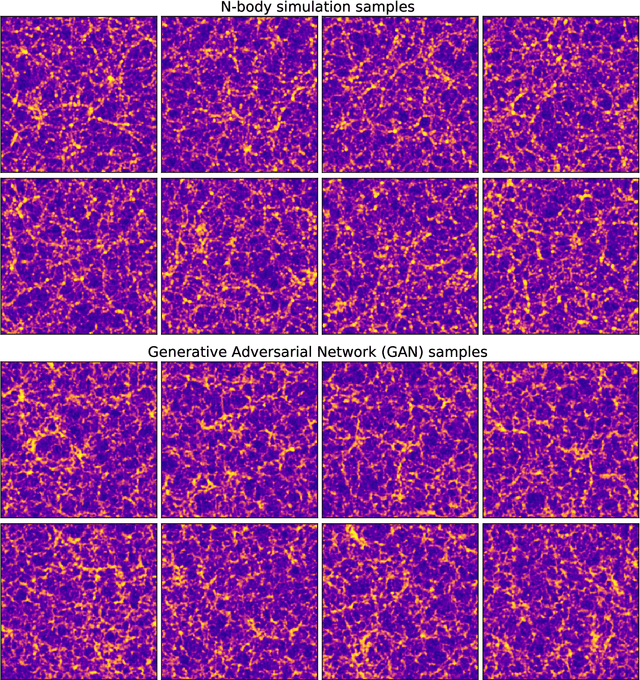
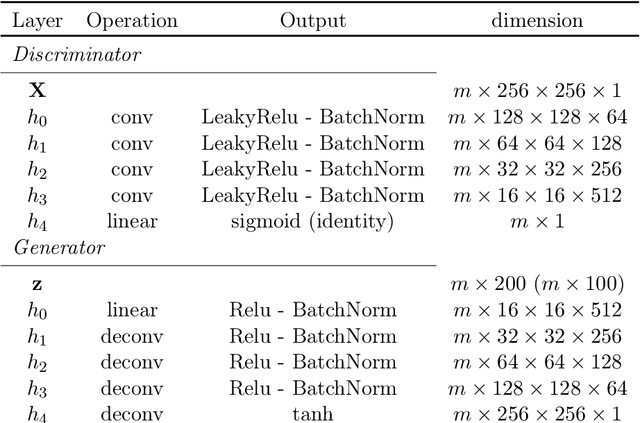
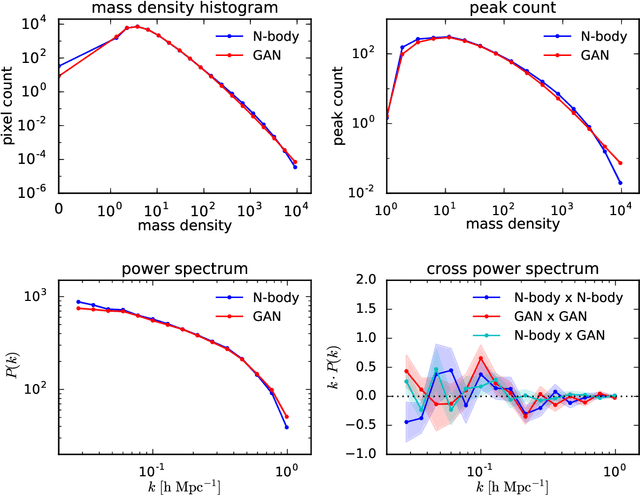
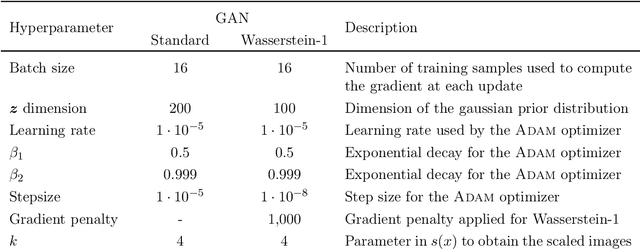
Abstract:Dark matter in the universe evolves through gravity to form a complex network of halos, filaments, sheets and voids, that is known as the cosmic web. Computational models of the underlying physical processes, such as classical N-body simulations, are extremely resource intensive, as they track the action of gravity in an expanding universe using billions of particles as tracers of the cosmic matter distribution. Therefore, upcoming cosmology experiments will face a computational bottleneck that may limit the exploitation of their full scientific potential. To address this challenge, we demonstrate the application of a machine learning technique called Generative Adversarial Networks (GAN) to learn models that can efficiently generate new, physically realistic realizations of the cosmic web. Our training set is a small, representative sample of 2D image snapshots from N-body simulations of size 500 and 100 Mpc. We show that the GAN-produced results are qualitatively and quantitatively very similar to the originals. Generation of a new cosmic web realization with a GAN takes a fraction of a second, compared to the many hours needed by the N-body technique. We anticipate that GANs will therefore play an important role in providing extremely fast and precise simulations of cosmic web in the era of large cosmological surveys, such as Euclid and LSST.
Cosmological model discrimination with Deep Learning
Jul 18, 2017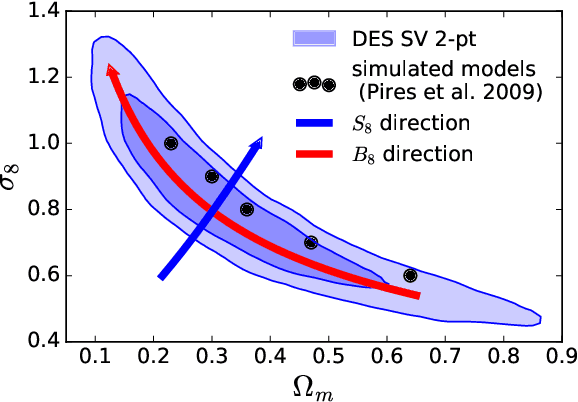
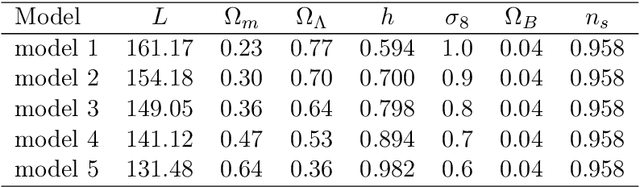

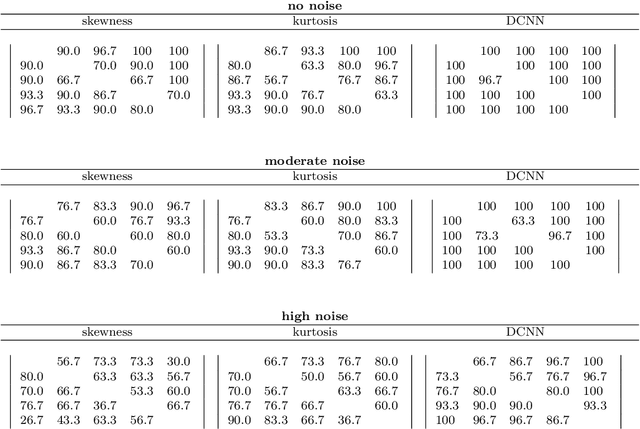
Abstract:We demonstrate the potential of Deep Learning methods for measurements of cosmological parameters from density fields, focusing on the extraction of non-Gaussian information. We consider weak lensing mass maps as our dataset. We aim for our method to be able to distinguish between five models, which were chosen to lie along the $\sigma_8$ - $\Omega_m$ degeneracy, and have nearly the same two-point statistics. We design and implement a Deep Convolutional Neural Network (DCNN) which learns the relation between five cosmological models and the mass maps they generate. We develop a new training strategy which ensures the good performance of the network for high levels of noise. We compare the performance of this approach to commonly used non-Gaussian statistics, namely the skewness and kurtosis of the convergence maps. We find that our implementation of DCNN outperforms the skewness and kurtosis statistics, especially for high noise levels. The network maintains the mean discrimination efficiency greater than $85\%$ even for noise levels corresponding to ground based lensing observations, while the other statistics perform worse in this setting, achieving efficiency less than $70\%$. This demonstrates the ability of CNN-based methods to efficiently break the $\sigma_8$ - $\Omega_m$ degeneracy with weak lensing mass maps alone. We discuss the potential of this method to be applied to the analysis of real weak lensing data and other datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge