NeuroSteiner: A Graph Transformer for Wirelength Estimation

A core objective of physical design is to minimize wirelength (WL) when placing chip components on a canvas. Computing the minimal WL of a placement requires finding rectilinear Steiner minimum trees (RSMTs), an NP-hard problem. We propose NeuroSteiner, a neural model that distills GeoSteiner, an optimal RSMT solver, to navigate the cost--accuracy frontier of WL estimation. NeuroSteiner is trained on synthesized nets labeled by GeoSteiner, alleviating the need to train on real chip designs. Moreover, NeuroSteiner's differentiability allows to place by minimizing WL through gradient descent. On ISPD 2005 and 2019, NeuroSteiner can obtain 0.3% WL error while being 60% faster than GeoSteiner, or 0.2% and 30%.

CodeIt: Self-Improving Language Models with Prioritized Hindsight Replay

Large language models are increasingly solving tasks that are commonly believed to require human-level reasoning ability. However, these models still perform very poorly on benchmarks of general intelligence such as the Abstraction and Reasoning Corpus (ARC). In this paper, we approach ARC as a programming-by-examples problem, and introduce a novel and scalable method for language model self-improvement called Code Iteration (CodeIt). Our method iterates between 1) program sampling and hindsight relabeling, and 2) learning from prioritized experience replay. By relabeling the goal of an episode (i.e., the target program output given input) to the realized output produced by the sampled program, our method effectively deals with the extreme sparsity of rewards in program synthesis. Applying CodeIt to the ARC dataset, we demonstrate that prioritized hindsight replay, along with pre-training and data-augmentation, leads to successful inter-task generalization. CodeIt is the first neuro-symbolic approach that scales to the full ARC evaluation dataset. Our method solves 15% of ARC evaluation tasks, achieving state-of-the-art performance and outperforming existing neural and symbolic baselines.

ChebLieNet: Invariant Spectral Graph NNs Turned Equivariant by Riemannian Geometry on Lie Groups

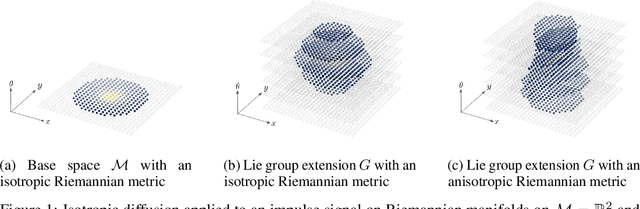
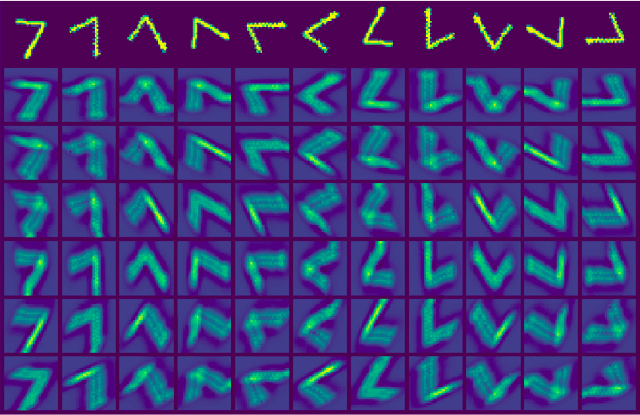
We introduce ChebLieNet, a group-equivariant method on (anisotropic) manifolds. Surfing on the success of graph- and group-based neural networks, we take advantage of the recent developments in the geometric deep learning field to derive a new approach to exploit any anisotropies in data. Via discrete approximations of Lie groups, we develop a graph neural network made of anisotropic convolutional layers (Chebyshev convolutions), spatial pooling and unpooling layers, and global pooling layers. Group equivariance is achieved via equivariant and invariant operators on graphs with anisotropic left-invariant Riemannian distance-based affinities encoded on the edges. Thanks to its simple form, the Riemannian metric can model any anisotropies, both in the spatial and orientation domains. This control on anisotropies of the Riemannian metrics allows to balance equivariance (anisotropic metric) against invariance (isotropic metric) of the graph convolution layers. Hence we open the doors to a better understanding of anisotropic properties. Furthermore, we empirically prove the existence of (data-dependent) sweet spots for anisotropic parameters on CIFAR10. This crucial result is evidence of the benefice we could get by exploiting anisotropic properties in data. We also evaluate the scalability of this approach on STL10 (image data) and ClimateNet (spherical data), showing its remarkable adaptability to diverse tasks.

Learning to recover orientations from projections in single-particle cryo-EM

A major challenge in single-particle cryo-electron microscopy (cryo-EM) is that the orientations adopted by the 3D particles prior to imaging are unknown; yet, this knowledge is essential for high-resolution reconstruction. We present a method to recover these orientations directly from the acquired set of 2D projections. Our approach consists of two steps: (i) the estimation of distances between pairs of projections, and (ii) the recovery of the orientation of each projection from these distances. In step (i), pairwise distances are estimated by a Siamese neural network trained on synthetic cryo-EM projections from resolved bio-structures. In step (ii), orientations are recovered by minimizing the difference between the distances estimated from the projections and the distances induced by the recovered orientations. We evaluated the method on synthetic cryo-EM datasets. Current results demonstrate that orientations can be accurately recovered from projections that are shifted and corrupted with a high level of noise. The accuracy of the recovery depends on the accuracy of the distance estimator. While not yet deployed in a real experimental setup, the proposed method offers a novel learning-based take on orientation recovery in SPA. Our code is available at https://github.com/JelenaBanjac/protein-reconstruction

DeepSphere: a graph-based spherical CNN

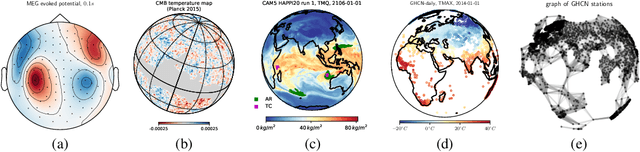
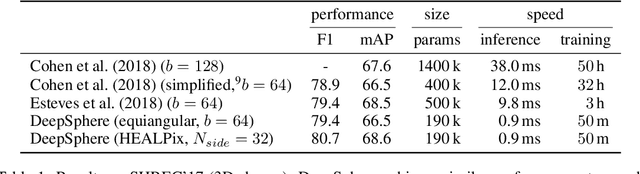
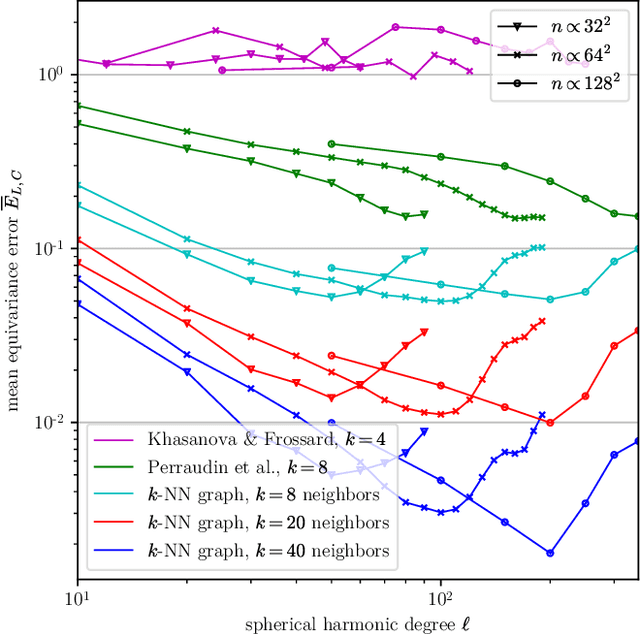
Designing a convolution for a spherical neural network requires a delicate tradeoff between efficiency and rotation equivariance. DeepSphere, a method based on a graph representation of the sampled sphere, strikes a controllable balance between these two desiderata. This contribution is twofold. First, we study both theoretically and empirically how equivariance is affected by the underlying graph with respect to the number of vertices and neighbors. Second, we evaluate DeepSphere on relevant problems. Experiments show state-of-the-art performance and demonstrates the efficiency and flexibility of this formulation. Perhaps surprisingly, comparison with previous work suggests that anisotropic filters might be an unnecessary price to pay. Our code is available at https://github.com/deepsphere

Simplicial Neural Networks

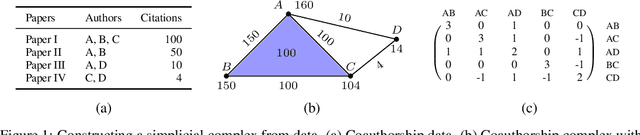
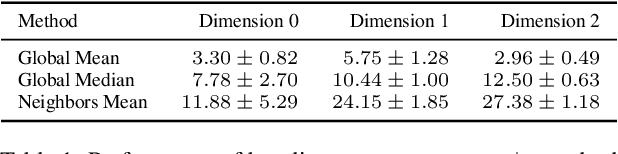
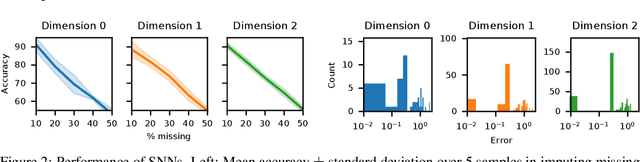
We present simplicial neural networks (SNNs), a generalization of graph neural networks to data that live on a class of topological spaces called simplicial complexes. These are natural multi-dimensional extensions of graphs that encode not only pairwise relationships but also higher-order interactions between vertices - allowing us to consider richer data, including vector fields and $n$-fold collaboration networks. We define an appropriate notion of convolution that we leverage to construct the desired convolutional neural networks. We test the SNNs on the task of imputing missing data on coauthorship complexes.

DeepSphere: towards an equivariant graph-based spherical CNN

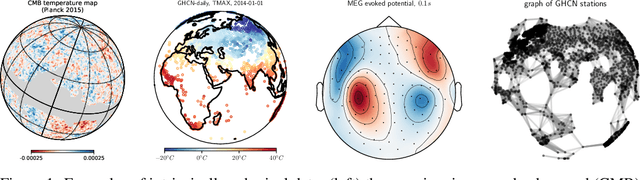
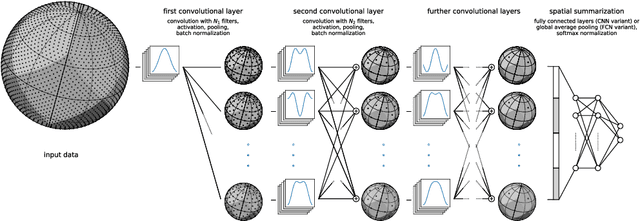
Spherical data is found in many applications. By modeling the discretized sphere as a graph, we can accommodate non-uniformly distributed, partial, and changing samplings. Moreover, graph convolutions are computationally more efficient than spherical convolutions. As equivariance is desired to exploit rotational symmetries, we discuss how to approach rotation equivariance using the graph neural network introduced in Defferrard et al. (2016). Experiments show good performance on rotation-invariant learning problems. Code and examples are available at https://github.com/SwissDataScienceCenter/DeepSphere

DeepSphere: Efficient spherical Convolutional Neural Network with HEALPix sampling for cosmological applications

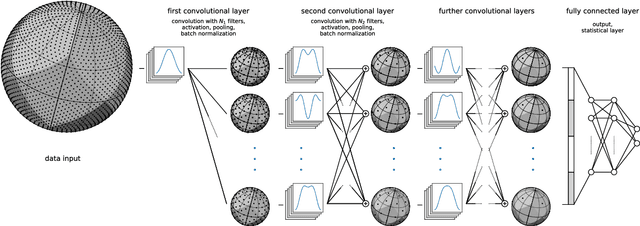
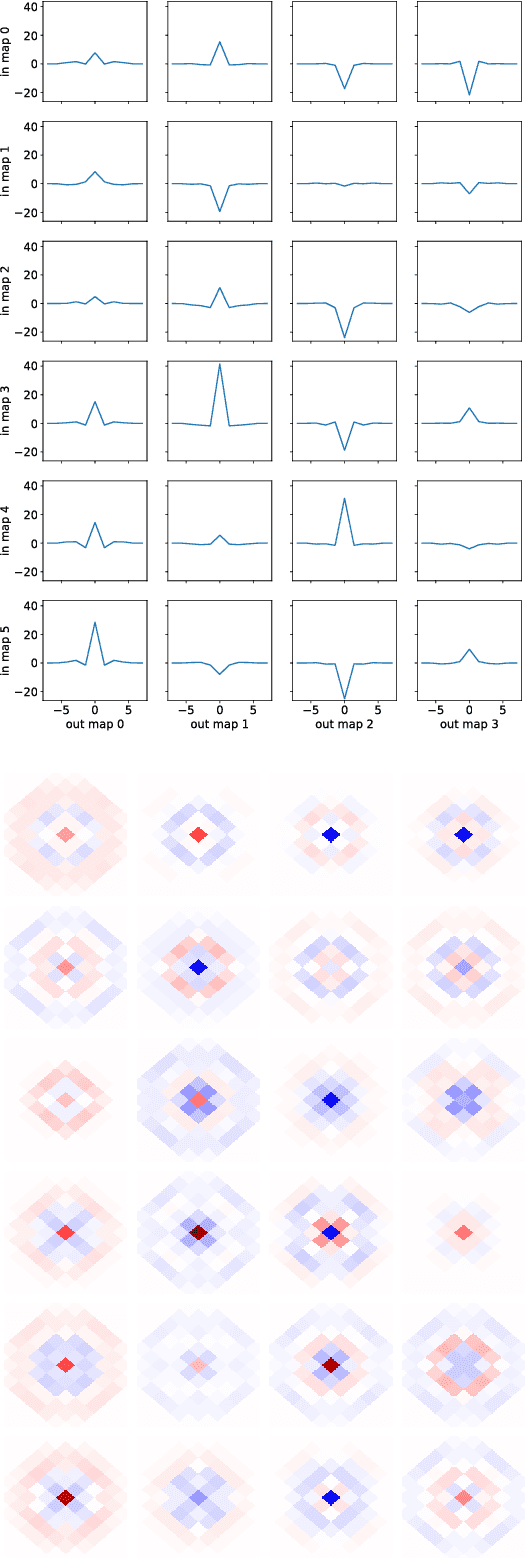
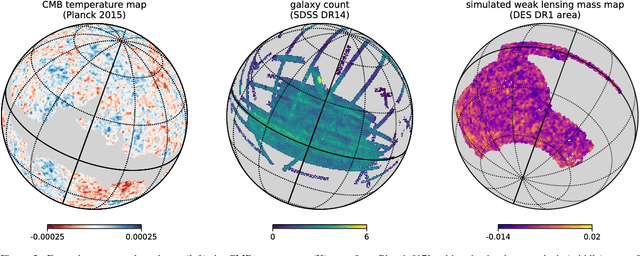
Convolutional Neural Networks (CNNs) are a cornerstone of the Deep Learning toolbox and have led to many breakthroughs in Artificial Intelligence. These networks have mostly been developed for regular Euclidean domains such as those supporting images, audio, or video. Because of their success, CNN-based methods are becoming increasingly popular in Cosmology. Cosmological data often comes as spherical maps, which make the use of the traditional CNNs more complicated. The commonly used pixelization scheme for spherical maps is the Hierarchical Equal Area isoLatitude Pixelisation (HEALPix). We present a spherical CNN for analysis of full and partial HEALPix maps, which we call DeepSphere. The spherical CNN is constructed by representing the sphere as a graph. Graphs are versatile data structures that can act as a discrete representation of a continuous manifold. Using the graph-based representation, we define many of the standard CNN operations, such as convolution and pooling. With filters restricted to being radial, our convolutions are equivariant to rotation on the sphere, and DeepSphere can be made invariant or equivariant to rotation. This way, DeepSphere is a special case of a graph CNN, tailored to the HEALPix sampling of the sphere. This approach is computationally more efficient than using spherical harmonics to perform convolutions. We demonstrate the method on a classification problem of weak lensing mass maps from two cosmological models and compare the performance of the CNN with that of two baseline classifiers. The results show that the performance of DeepSphere is always superior or equal to both of these baselines. For high noise levels and for data covering only a smaller fraction of the sphere, DeepSphere achieves typically 10% better classification accuracy than those baselines. Finally, we show how learned filters can be visualized to introspect the neural network.

Learning to Recognize Musical Genre from Audio

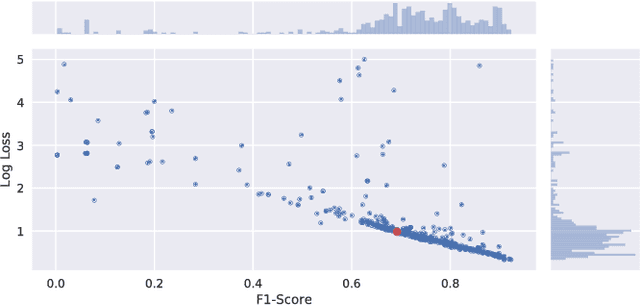
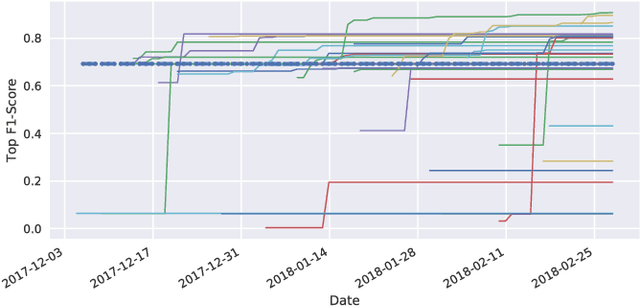
We here summarize our experience running a challenge with open data for musical genre recognition. Those notes motivate the task and the challenge design, show some statistics about the submissions, and present the results.

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering

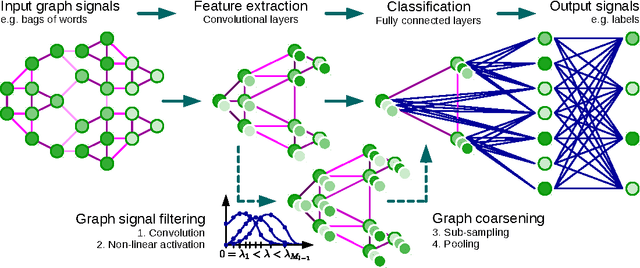
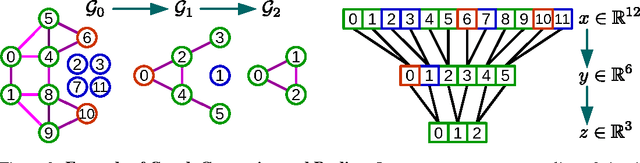
In this work, we are interested in generalizing convolutional neural networks (CNNs) from low-dimensional regular grids, where image, video and speech are represented, to high-dimensional irregular domains, such as social networks, brain connectomes or words' embedding, represented by graphs. We present a formulation of CNNs in the context of spectral graph theory, which provides the necessary mathematical background and efficient numerical schemes to design fast localized convolutional filters on graphs. Importantly, the proposed technique offers the same linear computational complexity and constant learning complexity as classical CNNs, while being universal to any graph structure. Experiments on MNIST and 20NEWS demonstrate the ability of this novel deep learning system to learn local, stationary, and compositional features on graphs.