Gard Spreemann
Simplicial Neural Networks
Oct 07, 2020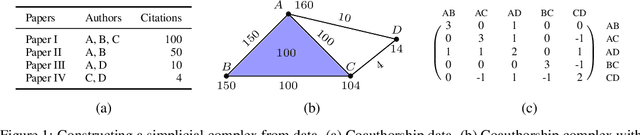


Abstract:We present simplicial neural networks (SNNs), a generalization of graph neural networks to data that live on a class of topological spaces called simplicial complexes. These are natural multi-dimensional extensions of graphs that encode not only pairwise relationships but also higher-order interactions between vertices - allowing us to consider richer data, including vector fields and $n$-fold collaboration networks. We define an appropriate notion of convolution that we leverage to construct the desired convolutional neural networks. We test the SNNs on the task of imputing missing data on coauthorship complexes.
A Notion of Harmonic Clustering in Simplicial Complexes
Oct 16, 2019

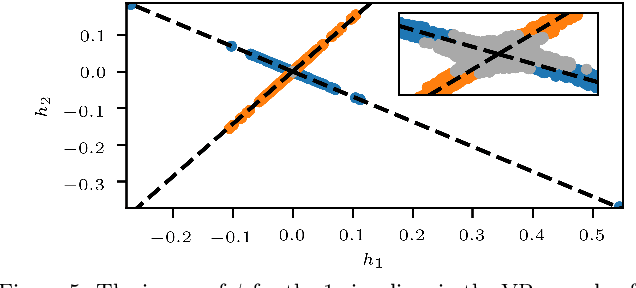
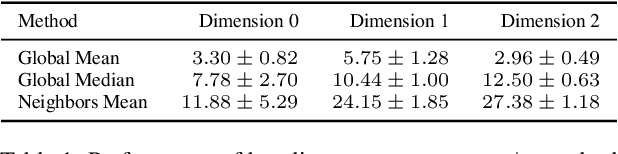
Abstract:We outline a novel clustering scheme for simplicial complexes that produces clusters of simplices in a way that is sensitive to the homology of the complex. The method is inspired by, and can be seen as a higher-dimensional version of, graph spectral clustering. The algorithm involves only sparse eigenproblems, and is therefore computationally efficient. We believe that it has broad application as a way to extract features from simplicial complexes that often arise in topological data analysis.
Topology of Learning in Artificial Neural Networks
Feb 21, 2019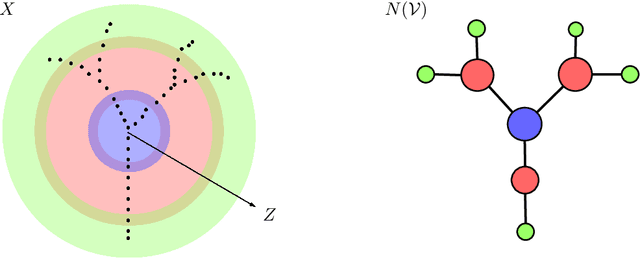
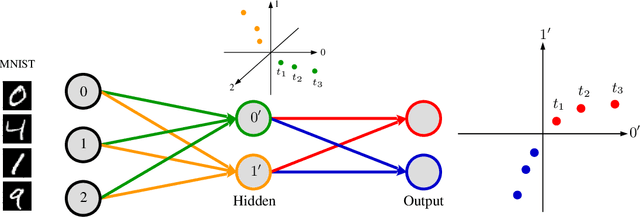
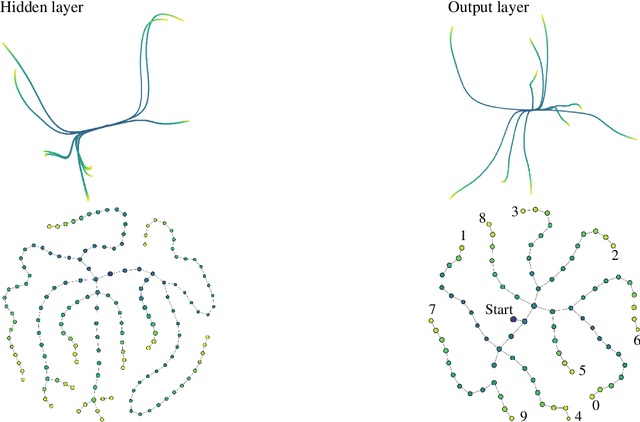
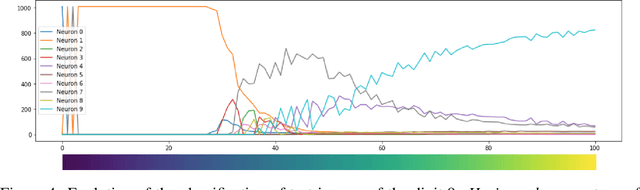
Abstract:Understanding how neural networks learn remains one of the central challenges in machine learning research. From random at the start of training, the weights of a neural network evolve in such a way as to be able to perform a variety of tasks, like classifying images. Here we study the emergence of structure in the weights by applying methods from topological data analysis. We train simple feedforward neural networks on the MNIST dataset and monitor the evolution of the weights. When initialized to zero, the weights follow trajectories that branch off recurrently, thus generating trees that describe the growth of the effective capacity of each layer. When initialized to tiny random values, the weights evolve smoothly along two-dimensional surfaces. We show that natural coordinates on these learning surfaces correspond to important factors of variation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge