A Notion of Harmonic Clustering in Simplicial Complexes
Paper and Code
Oct 16, 2019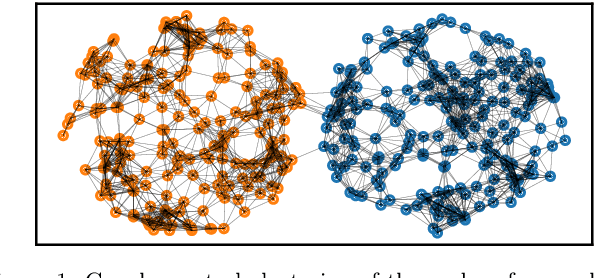
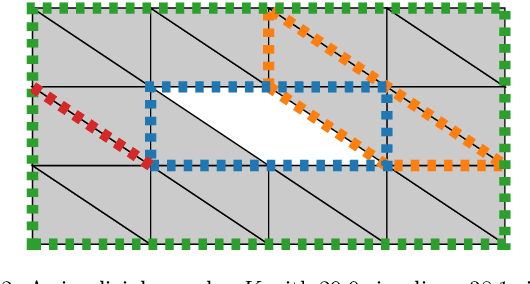

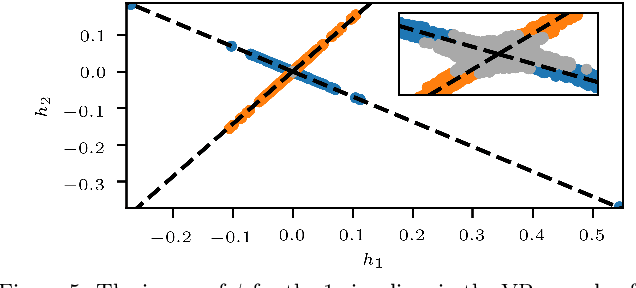
We outline a novel clustering scheme for simplicial complexes that produces clusters of simplices in a way that is sensitive to the homology of the complex. The method is inspired by, and can be seen as a higher-dimensional version of, graph spectral clustering. The algorithm involves only sparse eigenproblems, and is therefore computationally efficient. We believe that it has broad application as a way to extract features from simplicial complexes that often arise in topological data analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge