Laue Indexing with Optimal Transport

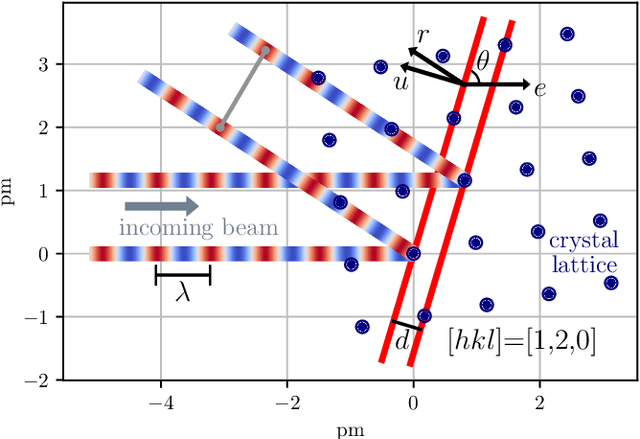
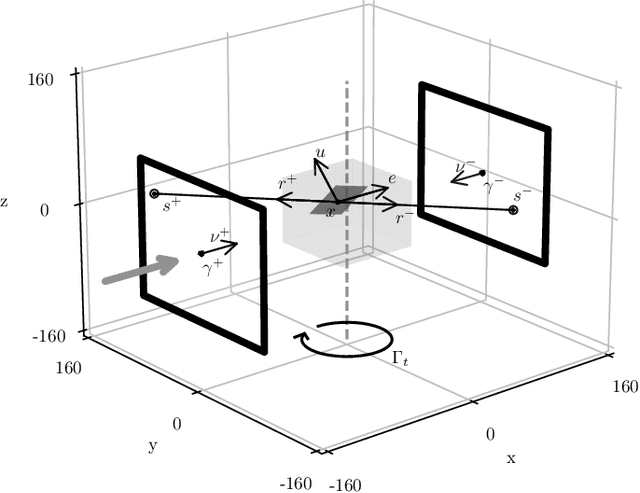
Laue tomography experiments retrieve the positions and orientations of crystal grains in a polycrystalline samples from diffraction patterns recorded at multiple viewing angles. The use of a broad wavelength spectrum beam can greatly reduce the experimental time, but poses a difficult challenge for the indexing of diffraction peaks in polycrystalline samples; the information about the wavelength of these Bragg peaks is absent and the diffraction patterns from multiple grains are superimposed. To date, no algorithms exist capable of indexing samples with more than about 500 grains efficiently. To address this need we present a novel method: Laue indexing with Optimal Transport (LaueOT). We create a probabilistic description of the multi-grain indexing problem and propose a solution based on Sinkhorn Expectation-Maximization method, which allows to efficiently find the maximum of the likelihood thanks to the assignments being calculated using Optimal Transport. This is a non-convex optimization problem, where the orientations and positions of grains are optimized simultaneously with grain-to-spot assignments, while robustly handling the outliers. The selection of initial prototype grains to consider in the optimization problem are also calculated within the Optimal Transport framework. LaueOT can rapidly and effectively index up to 1000 grains on a single large memory GPU within less than 30 minutes. We demonstrate the performance of LaueOT on simulations with variable numbers of grains, spot position measurement noise levels, and outlier fractions. The algorithm recovers the correct number of grains even for high noise levels and up to 70% outliers in our experiments. We compare the results of indexing with LaueOT to existing algorithms both on synthetic and real neutron diffraction data from well-characterized samples.