Towards solving model bias in cosmic shear forward modeling

As the volume and quality of modern galaxy surveys increase, so does the difficulty of measuring the cosmological signal imprinted in galaxy shapes. Weak gravitational lensing sourced by the most massive structures in the Universe generates a slight shearing of galaxy morphologies called cosmic shear, key probe for cosmological models. Modern techniques of shear estimation based on statistics of ellipticity measurements suffer from the fact that the ellipticity is not a well-defined quantity for arbitrary galaxy light profiles, biasing the shear estimation. We show that a hybrid physical and deep learning Hierarchical Bayesian Model, where a generative model captures the galaxy morphology, enables us to recover an unbiased estimate of the shear on realistic galaxies, thus solving the model bias.

Neural Posterior Estimation with Differentiable Simulators

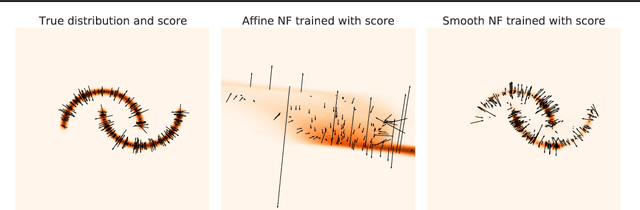
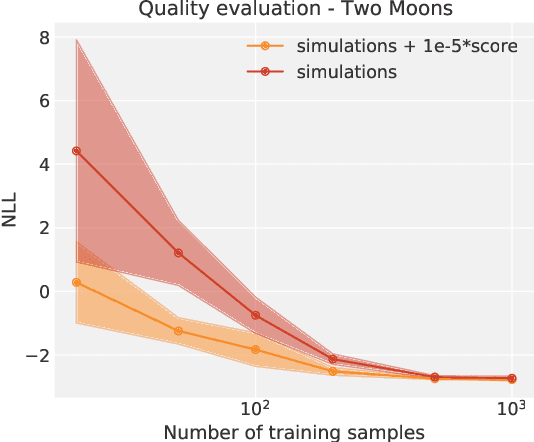
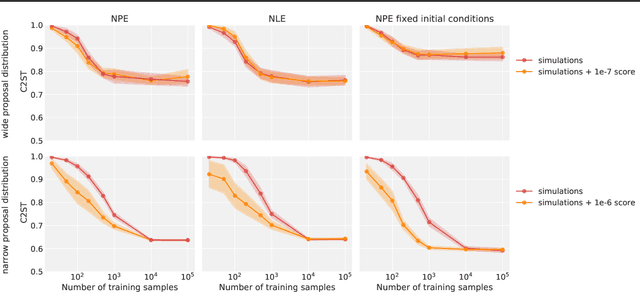
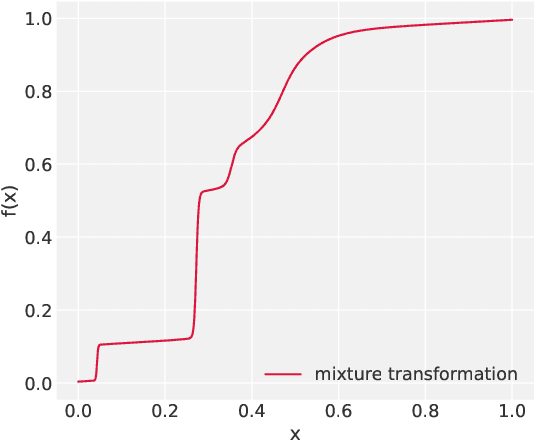
Simulation-Based Inference (SBI) is a promising Bayesian inference framework that alleviates the need for analytic likelihoods to estimate posterior distributions. Recent advances using neural density estimators in SBI algorithms have demonstrated the ability to achieve high-fidelity posteriors, at the expense of a large number of simulations ; which makes their application potentially very time-consuming when using complex physical simulations. In this work we focus on boosting the sample-efficiency of posterior density estimation using the gradients of the simulator. We present a new method to perform Neural Posterior Estimation (NPE) with a differentiable simulator. We demonstrate how gradient information helps constrain the shape of the posterior and improves sample-efficiency.

Probabilistic Mass Mapping with Neural Score Estimation

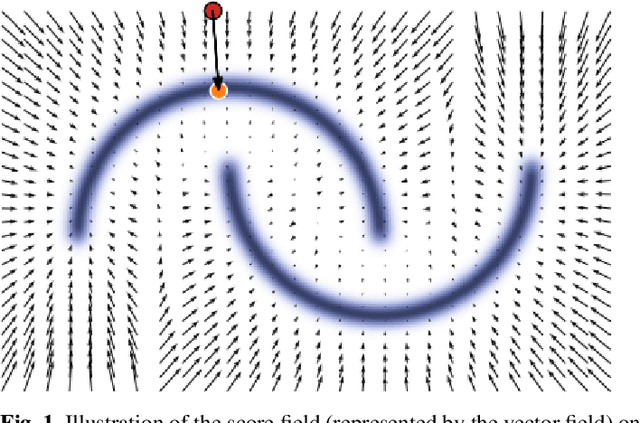
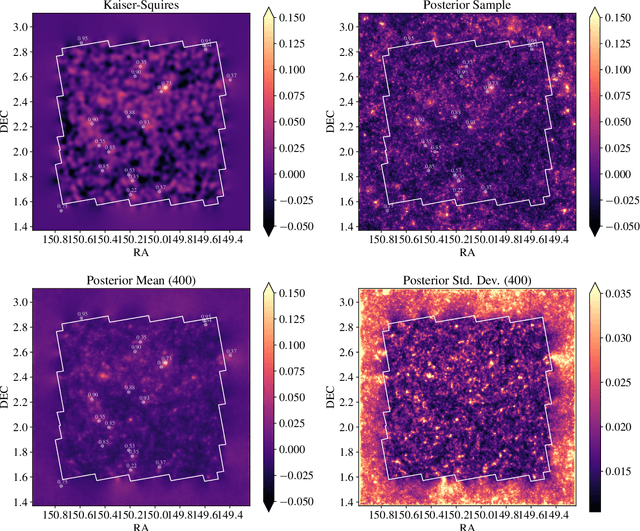
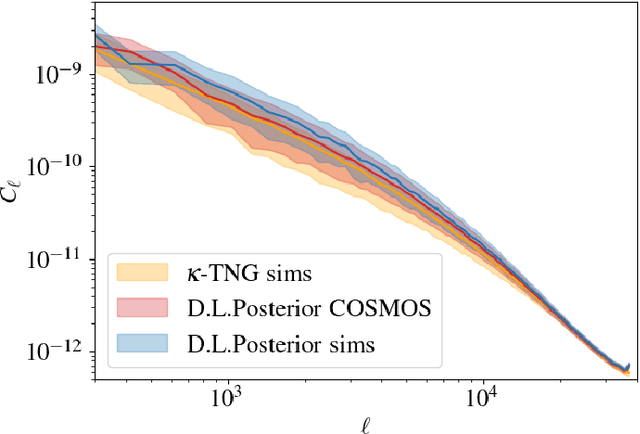
Weak lensing mass-mapping is a useful tool to access the full distribution of dark matter on the sky, but because of intrinsic galaxy ellipticies and finite fields/missing data, the recovery of dark matter maps constitutes a challenging ill-posed inverse problem. We introduce a novel methodology allowing for efficient sampling of the high-dimensional Bayesian posterior of the weak lensing mass-mapping problem, and relying on simulations for defining a fully non-Gaussian prior. We aim to demonstrate the accuracy of the method on simulations, and then proceed to applying it to the mass reconstruction of the HST/ACS COSMOS field. The proposed methodology combines elements of Bayesian statistics, analytic theory, and a recent class of Deep Generative Models based on Neural Score Matching. This approach allows us to do the following: 1) Make full use of analytic cosmological theory to constrain the 2pt statistics of the solution. 2) Learn from cosmological simulations any differences between this analytic prior and full simulations. 3) Obtain samples from the full Bayesian posterior of the problem for robust Uncertainty Quantification. We demonstrate the method on the $\kappa$TNG simulations and find that the posterior mean significantly outperfoms previous methods (Kaiser-Squires, Wiener filter, Sparsity priors) both on root-mean-square error and in terms of the Pearson correlation. We further illustrate the interpretability of the recovered posterior by establishing a close correlation between posterior convergence values and SNR of clusters artificially introduced into a field. Finally, we apply the method to the reconstruction of the HST/ACS COSMOS field and yield the highest quality convergence map of this field to date.

Denoising Score-Matching for Uncertainty Quantification in Inverse Problems

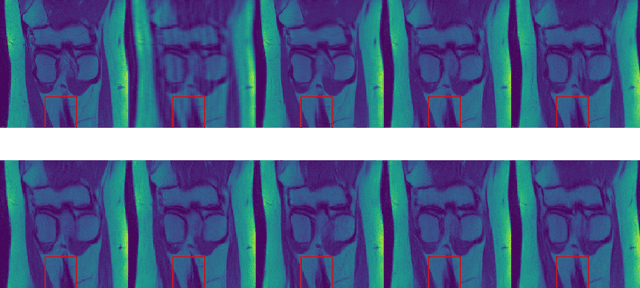
Deep neural networks have proven extremely efficient at solving a wide rangeof inverse problems, but most often the uncertainty on the solution they provideis hard to quantify. In this work, we propose a generic Bayesian framework forsolving inverse problems, in which we limit the use of deep neural networks tolearning a prior distribution on the signals to recover. We adopt recent denoisingscore matching techniques to learn this prior from data, and subsequently use it aspart of an annealed Hamiltonian Monte-Carlo scheme to sample the full posteriorof image inverse problems. We apply this framework to Magnetic ResonanceImage (MRI) reconstruction and illustrate how this approach not only yields highquality reconstructions but can also be used to assess the uncertainty on particularfeatures of a reconstructed image.