Bayesian Deconvolution of Astronomical Images with Diffusion Models: Quantifying Prior-Driven Features in Reconstructions

Deconvolution of astronomical images is a key aspect of recovering the intrinsic properties of celestial objects, especially when considering ground-based observations. This paper explores the use of diffusion models (DMs) and the Diffusion Posterior Sampling (DPS) algorithm to solve this inverse problem task. We apply score-based DMs trained on high-resolution cosmological simulations, through a Bayesian setting to compute a posterior distribution given the observations available. By considering the redshift and the pixel scale as parameters of our inverse problem, the tool can be easily adapted to any dataset. We test our model on Hyper Supreme Camera (HSC) data and show that we reach resolutions comparable to those obtained by Hubble Space Telescope (HST) images. Most importantly, we quantify the uncertainty of reconstructions and propose a metric to identify prior-driven features in the reconstructed images, which is key in view of applying these methods for scientific purposes.

Neural Posterior Estimation with Differentiable Simulators

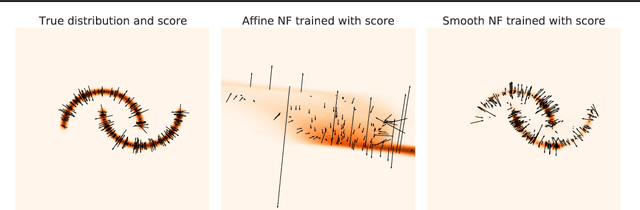
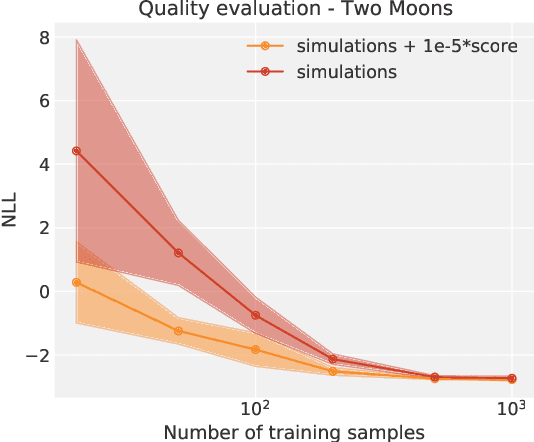
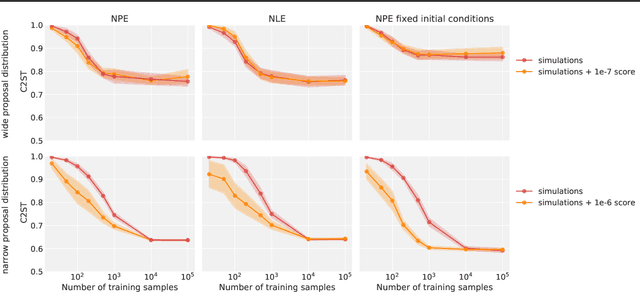
Simulation-Based Inference (SBI) is a promising Bayesian inference framework that alleviates the need for analytic likelihoods to estimate posterior distributions. Recent advances using neural density estimators in SBI algorithms have demonstrated the ability to achieve high-fidelity posteriors, at the expense of a large number of simulations ; which makes their application potentially very time-consuming when using complex physical simulations. In this work we focus on boosting the sample-efficiency of posterior density estimation using the gradients of the simulator. We present a new method to perform Neural Posterior Estimation (NPE) with a differentiable simulator. We demonstrate how gradient information helps constrain the shape of the posterior and improves sample-efficiency.