Neural Posterior Estimation with Differentiable Simulators
Paper and Code
Jul 12, 2022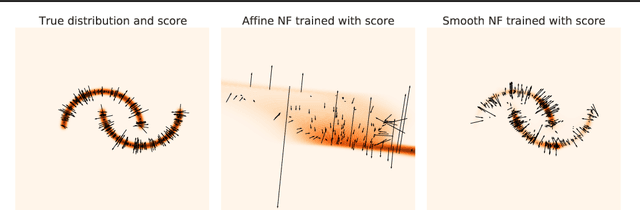
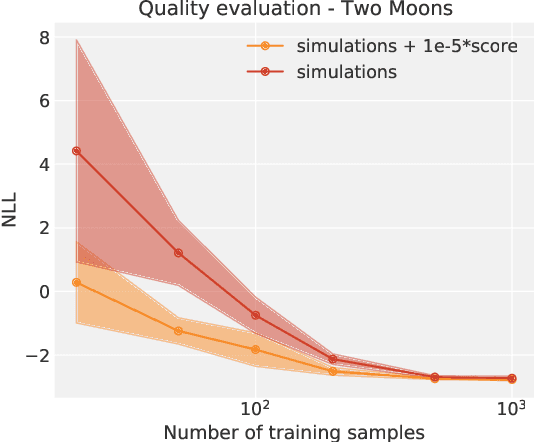

Simulation-Based Inference (SBI) is a promising Bayesian inference framework that alleviates the need for analytic likelihoods to estimate posterior distributions. Recent advances using neural density estimators in SBI algorithms have demonstrated the ability to achieve high-fidelity posteriors, at the expense of a large number of simulations ; which makes their application potentially very time-consuming when using complex physical simulations. In this work we focus on boosting the sample-efficiency of posterior density estimation using the gradients of the simulator. We present a new method to perform Neural Posterior Estimation (NPE) with a differentiable simulator. We demonstrate how gradient information helps constrain the shape of the posterior and improves sample-efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge