Evidence Networks: simple losses for fast, amortized, neural Bayesian model comparison

Evidence Networks can enable Bayesian model comparison when state-of-the-art methods (e.g. nested sampling) fail and even when likelihoods or priors are intractable or unknown. Bayesian model comparison, i.e. the computation of Bayes factors or evidence ratios, can be cast as an optimization problem. Though the Bayesian interpretation of optimal classification is well-known, here we change perspective and present classes of loss functions that result in fast, amortized neural estimators that directly estimate convenient functions of the Bayes factor. This mitigates numerical inaccuracies associated with estimating individual model probabilities. We introduce the leaky parity-odd power (l-POP) transform, leading to the novel ``l-POP-Exponential'' loss function. We explore neural density estimation for data probability in different models, showing it to be less accurate and scalable than Evidence Networks. Multiple real-world and synthetic examples illustrate that Evidence Networks are explicitly independent of dimensionality of the parameter space and scale mildly with the complexity of the posterior probability density function. This simple yet powerful approach has broad implications for model inference tasks. As an application of Evidence Networks to real-world data we compute the Bayes factor for two models with gravitational lensing data of the Dark Energy Survey. We briefly discuss applications of our methods to other, related problems of model comparison and evaluation in implicit inference settings.

Rediscovering orbital mechanics with machine learning

We present an approach for using machine learning to automatically discover the governing equations and hidden properties of real physical systems from observations. We train a "graph neural network" to simulate the dynamics of our solar system's Sun, planets, and large moons from 30 years of trajectory data. We then use symbolic regression to discover an analytical expression for the force law implicitly learned by the neural network, which our results showed is equivalent to Newton's law of gravitation. The key assumptions that were required were translational and rotational equivariance, and Newton's second and third laws of motion. Our approach correctly discovered the form of the symbolic force law. Furthermore, our approach did not require any assumptions about the masses of planets and moons or physical constants. They, too, were accurately inferred through our methods. Though, of course, the classical law of gravitation has been known since Isaac Newton, our result serves as a validation that our method can discover unknown laws and hidden properties from observed data. More broadly this work represents a key step toward realizing the potential of machine learning for accelerating scientific discovery.

Probabilistic Mass Mapping with Neural Score Estimation

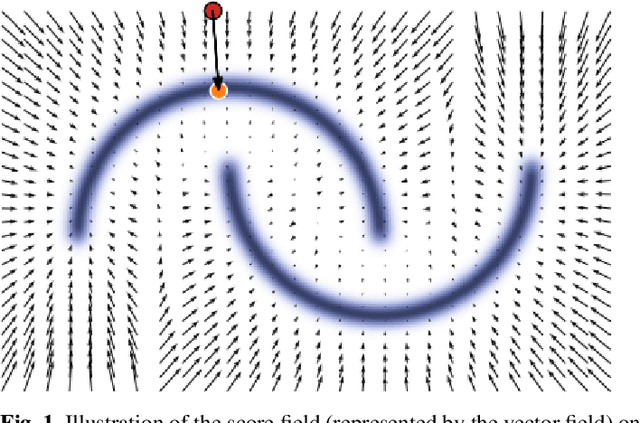
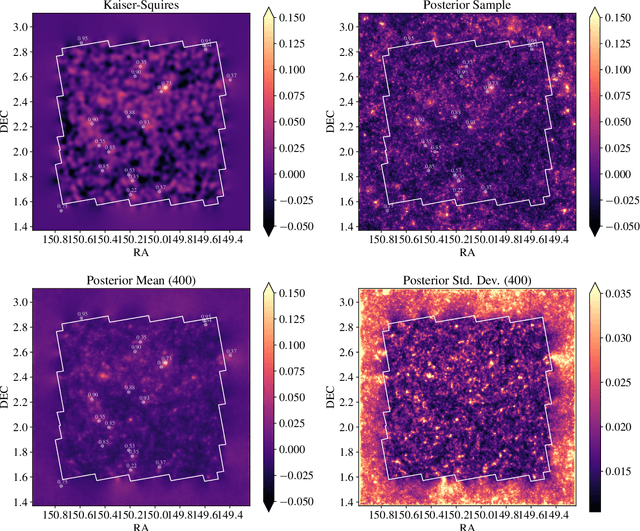
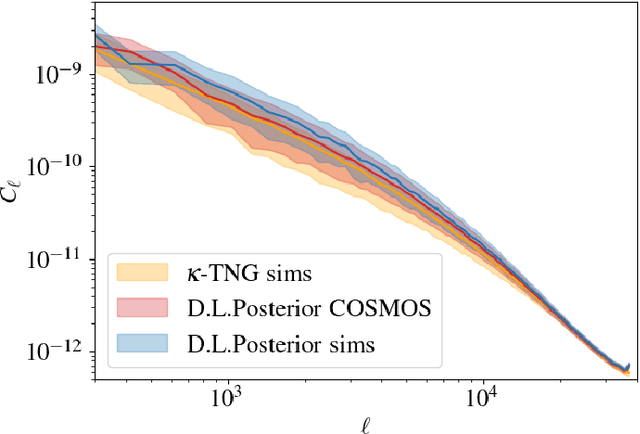
Weak lensing mass-mapping is a useful tool to access the full distribution of dark matter on the sky, but because of intrinsic galaxy ellipticies and finite fields/missing data, the recovery of dark matter maps constitutes a challenging ill-posed inverse problem. We introduce a novel methodology allowing for efficient sampling of the high-dimensional Bayesian posterior of the weak lensing mass-mapping problem, and relying on simulations for defining a fully non-Gaussian prior. We aim to demonstrate the accuracy of the method on simulations, and then proceed to applying it to the mass reconstruction of the HST/ACS COSMOS field. The proposed methodology combines elements of Bayesian statistics, analytic theory, and a recent class of Deep Generative Models based on Neural Score Matching. This approach allows us to do the following: 1) Make full use of analytic cosmological theory to constrain the 2pt statistics of the solution. 2) Learn from cosmological simulations any differences between this analytic prior and full simulations. 3) Obtain samples from the full Bayesian posterior of the problem for robust Uncertainty Quantification. We demonstrate the method on the $\kappa$TNG simulations and find that the posterior mean significantly outperfoms previous methods (Kaiser-Squires, Wiener filter, Sparsity priors) both on root-mean-square error and in terms of the Pearson correlation. We further illustrate the interpretability of the recovered posterior by establishing a close correlation between posterior convergence values and SNR of clusters artificially introduced into a field. Finally, we apply the method to the reconstruction of the HST/ACS COSMOS field and yield the highest quality convergence map of this field to date.

Solving high-dimensional parameter inference: marginal posterior densities & Moment Networks

High-dimensional probability density estimation for inference suffers from the "curse of dimensionality". For many physical inference problems, the full posterior distribution is unwieldy and seldom used in practice. Instead, we propose direct estimation of lower-dimensional marginal distributions, bypassing high-dimensional density estimation or high-dimensional Markov chain Monte Carlo (MCMC) sampling. By evaluating the two-dimensional marginal posteriors we can unveil the full-dimensional parameter covariance structure. We additionally propose constructing a simple hierarchy of fast neural regression models, called Moment Networks, that compute increasing moments of any desired lower-dimensional marginal posterior density; these reproduce exact results from analytic posteriors and those obtained from Masked Autoregressive Flows. We demonstrate marginal posterior density estimation using high-dimensional LIGO-like gravitational wave time series and describe applications for problems of fundamental cosmology.