Walrus: A Cross-Domain Foundation Model for Continuum Dynamics

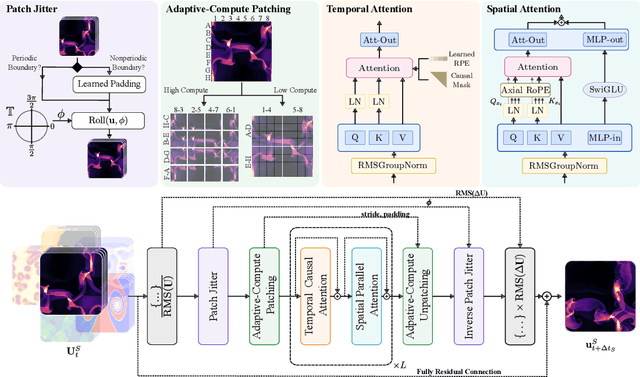
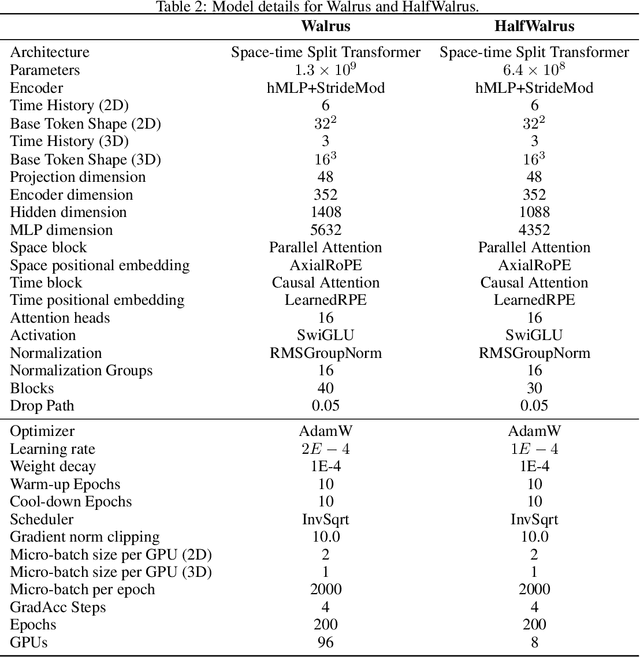
Foundation models have transformed machine learning for language and vision, but achieving comparable impact in physical simulation remains a challenge. Data heterogeneity and unstable long-term dynamics inhibit learning from sufficiently diverse dynamics, while varying resolutions and dimensionalities challenge efficient training on modern hardware. Through empirical and theoretical analysis, we incorporate new approaches to mitigate these obstacles, including a harmonic-analysis-based stabilization method, load-balanced distributed 2D and 3D training strategies, and compute-adaptive tokenization. Using these tools, we develop Walrus, a transformer-based foundation model developed primarily for fluid-like continuum dynamics. Walrus is pretrained on nineteen diverse scenarios spanning astrophysics, geoscience, rheology, plasma physics, acoustics, and classical fluids. Experiments show that Walrus outperforms prior foundation models on both short and long term prediction horizons on downstream tasks and across the breadth of pretraining data, while ablation studies confirm the value of our contributions to forecast stability, training throughput, and transfer performance over conventional approaches. Code and weights are released for community use.

The Well: a Large-Scale Collection of Diverse Physics Simulations for Machine Learning

Machine learning based surrogate models offer researchers powerful tools for accelerating simulation-based workflows. However, as standard datasets in this space often cover small classes of physical behavior, it can be difficult to evaluate the efficacy of new approaches. To address this gap, we introduce the Well: a large-scale collection of datasets containing numerical simulations of a wide variety of spatiotemporal physical systems. The Well draws from domain experts and numerical software developers to provide 15TB of data across 16 datasets covering diverse domains such as biological systems, fluid dynamics, acoustic scattering, as well as magneto-hydrodynamic simulations of extra-galactic fluids or supernova explosions. These datasets can be used individually or as part of a broader benchmark suite. To facilitate usage of the Well, we provide a unified PyTorch interface for training and evaluating models. We demonstrate the function of this library by introducing example baselines that highlight the new challenges posed by the complex dynamics of the Well. The code and data is available at https://github.com/PolymathicAI/the_well.

High Throughput Training of Deep Surrogates from Large Ensemble Runs

Recent years have seen a surge in deep learning approaches to accelerate numerical solvers, which provide faithful but computationally intensive simulations of the physical world. These deep surrogates are generally trained in a supervised manner from limited amounts of data slowly generated by the same solver they intend to accelerate. We propose an open-source framework that enables the online training of these models from a large ensemble run of simulations. It leverages multiple levels of parallelism to generate rich datasets. The framework avoids I/O bottlenecks and storage issues by directly streaming the generated data. A training reservoir mitigates the inherent bias of streaming while maximizing GPU throughput. Experiment on training a fully connected network as a surrogate for the heat equation shows the proposed approach enables training on 8TB of data in 2 hours with an accuracy improved by 47% and a batch throughput multiplied by 13 compared to a traditional offline procedure.

Training Deep Surrogate Models with Large Scale Online Learning

The spatiotemporal resolution of Partial Differential Equations (PDEs) plays important roles in the mathematical description of the world's physical phenomena. In general, scientists and engineers solve PDEs numerically by the use of computationally demanding solvers. Recently, deep learning algorithms have emerged as a viable alternative for obtaining fast solutions for PDEs. Models are usually trained on synthetic data generated by solvers, stored on disk and read back for training. This paper advocates that relying on a traditional static dataset to train these models does not allow the full benefit of the solver to be used as a data generator. It proposes an open source online training framework for deep surrogate models. The framework implements several levels of parallelism focused on simultaneously generating numerical simulations and training deep neural networks. This approach suppresses the I/O and storage bottleneck associated with disk-loaded datasets, and opens the way to training on significantly larger datasets. Experiments compare the offline and online training of four surrogate models, including state-of-the-art architectures. Results indicate that exposing deep surrogate models to more dataset diversity, up to hundreds of GB, can increase model generalization capabilities. Fully connected neural networks, Fourier Neural Operator (FNO), and Message Passing PDE Solver prediction accuracy is improved by 68%, 16% and 7%, respectively.

Simulation-Based Parallel Training

Numerical simulations are ubiquitous in science and engineering. Machine learning for science investigates how artificial neural architectures can learn from these simulations to speed up scientific discovery and engineering processes. Most of these architectures are trained in a supervised manner. They require tremendous amounts of data from simulations that are slow to generate and memory greedy. In this article, we present our ongoing work to design a training framework that alleviates those bottlenecks. It generates data in parallel with the training process. Such simultaneity induces a bias in the data available during the training. We present a strategy to mitigate this bias with a memory buffer. We test our framework on the multi-parametric Lorenz's attractor. We show the benefit of our framework compared to offline training and the success of our data bias mitigation strategy to capture the complex chaotic dynamics of the system.

Deep Surrogate for Direct Time Fluid Dynamics

The ubiquity of fluids in the physical world explains the need to accurately simulate their dynamics for many scientific and engineering applications. Traditionally, well established but resource intensive CFD solvers provide such simulations. The recent years have seen a surge of deep learning surrogate models substituting these solvers to alleviate the simulation process. Some approaches to build data-driven surrogates mimic the solver iterative process. They infer the next state of the fluid given its previous one. Others directly infer the state from time input. Approaches also differ in their management of the spatial information. Graph Neural Networks (GNN) can address the specificity of the irregular meshes commonly used in CFD simulations. In this article, we present our ongoing work to design a novel direct time GNN architecture for irregular meshes. It consists of a succession of graphs of increasing size connected by spline convolutions. We test our architecture on the Von K{\'a}rm{\'a}n's vortex street benchmark. It achieves small generalization errors while mitigating error accumulation along the trajectory.