Scattering Spectra Models for Physics

Physicists routinely need probabilistic models for a number of tasks such as parameter inference or the generation of new realizations of a field. Establishing such models for highly non-Gaussian fields is a challenge, especially when the number of samples is limited. In this paper, we introduce scattering spectra models for stationary fields and we show that they provide accurate and robust statistical descriptions of a wide range of fields encountered in physics. These models are based on covariances of scattering coefficients, i.e. wavelet decomposition of a field coupled with a point-wise modulus. After introducing useful dimension reductions taking advantage of the regularity of a field under rotation and scaling, we validate these models on various multi-scale physical fields and demonstrate that they reproduce standard statistics, including spatial moments up to 4th order. These scattering spectra provide us with a low-dimensional structured representation that captures key properties encountered in a wide range of physical fields. These generic models can be used for data exploration, classification, parameter inference, symmetry detection, and component separation.

How to quantify fields or textures? A guide to the scattering transform

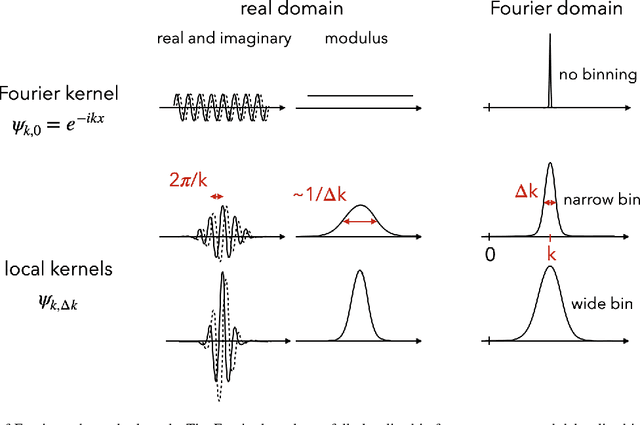
Extracting information from stochastic fields or textures is a ubiquitous task in science, from exploratory data analysis to classification and parameter estimation. From physics to biology, it tends to be done either through a power spectrum analysis, which is often too limited, or the use of convolutional neural networks (CNNs), which require large training sets and lack interpretability. In this paper, we advocate for the use of the scattering transform (Mallat 2012), a powerful statistic which borrows mathematical ideas from CNNs but does not require any training, and is interpretable. We show that it provides a relatively compact set of summary statistics with visual interpretation and which carries most of the relevant information in a wide range of scientific applications. We present a non-technical introduction to this estimator and we argue that it can benefit data analysis, comparison to models and parameter inference in many fields of science. Interestingly, understanding the core operations of the scattering transform allows one to decipher many key aspects of the inner workings of CNNs.