On the universality of neural encodings in CNNs

We explore the universality of neural encodings in convolutional neural networks trained on image classification tasks. We develop a procedure to directly compare the learned weights rather than their representations. It is based on a factorization of spatial and channel dimensions and measures the similarity of aligned weight covariances. We show that, for a range of layers of VGG-type networks, the learned eigenvectors appear to be universal across different natural image datasets. Our results suggest the existence of a universal neural encoding for natural images. They explain, at a more fundamental level, the success of transfer learning. Our work shows that, instead of aiming at maximizing the performance of neural networks, one can alternatively attempt to maximize the universality of the learned encoding, in order to build a principled foundation model.

Scattering Spectra Models for Physics

Physicists routinely need probabilistic models for a number of tasks such as parameter inference or the generation of new realizations of a field. Establishing such models for highly non-Gaussian fields is a challenge, especially when the number of samples is limited. In this paper, we introduce scattering spectra models for stationary fields and we show that they provide accurate and robust statistical descriptions of a wide range of fields encountered in physics. These models are based on covariances of scattering coefficients, i.e. wavelet decomposition of a field coupled with a point-wise modulus. After introducing useful dimension reductions taking advantage of the regularity of a field under rotation and scaling, we validate these models on various multi-scale physical fields and demonstrate that they reproduce standard statistics, including spatial moments up to 4th order. These scattering spectra provide us with a low-dimensional structured representation that captures key properties encountered in a wide range of physical fields. These generic models can be used for data exploration, classification, parameter inference, symmetry detection, and component separation.

A Rainbow in Deep Network Black Boxes

We introduce rainbow networks as a probabilistic model of trained deep neural networks. The model cascades random feature maps whose weight distributions are learned. It assumes that dependencies between weights at different layers are reduced to rotations which align the input activations. Neuron weights within a layer are independent after this alignment. Their activations define kernels which become deterministic in the infinite-width limit. This is verified numerically for ResNets trained on the ImageNet dataset. We also show that the learned weight distributions have low-rank covariances. Rainbow networks thus alternate between linear dimension reductions and non-linear high-dimensional embeddings with white random features. Gaussian rainbow networks are defined with Gaussian weight distributions. These models are validated numerically on image classification on the CIFAR-10 dataset, with wavelet scattering networks. We further show that during training, SGD updates the weight covariances while mostly preserving the Gaussian initialization.

How to quantify fields or textures? A guide to the scattering transform

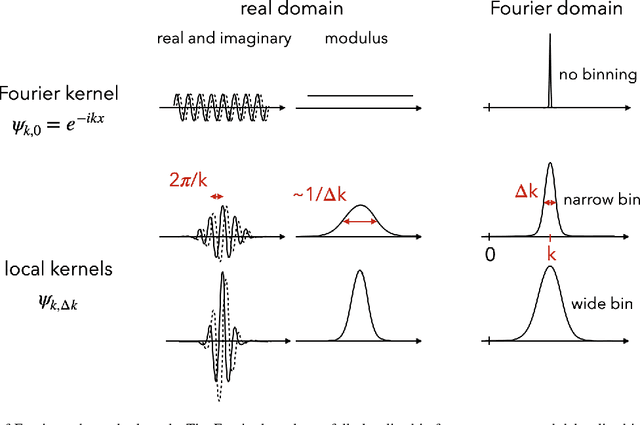
Extracting information from stochastic fields or textures is a ubiquitous task in science, from exploratory data analysis to classification and parameter estimation. From physics to biology, it tends to be done either through a power spectrum analysis, which is often too limited, or the use of convolutional neural networks (CNNs), which require large training sets and lack interpretability. In this paper, we advocate for the use of the scattering transform (Mallat 2012), a powerful statistic which borrows mathematical ideas from CNNs but does not require any training, and is interpretable. We show that it provides a relatively compact set of summary statistics with visual interpretation and which carries most of the relevant information in a wide range of scientific applications. We present a non-technical introduction to this estimator and we argue that it can benefit data analysis, comparison to models and parameter inference in many fields of science. Interestingly, understanding the core operations of the scattering transform allows one to decipher many key aspects of the inner workings of CNNs.

Sequencing seismograms: A panoptic view of scattering in the core-mantle boundary region

Scattering of seismic waves can reveal subsurface structures but usually in a piecemeal way focused on specific target areas. We used a manifold learning algorithm called "the Sequencer" to simultaneously analyze thousands of seismograms of waves diffracting along the core-mantle boundary and obtain a panoptic view of scattering across the Pacific region. In nearly half of the diffracting waveforms, we detected seismic waves scattered by three-dimensional structures near the core-mantle boundary. The prevalence of these scattered arrivals shows that the region hosts pervasive lateral heterogeneity. Our analysis revealed loud signals due to a plume root beneath Hawaii and a previously unrecognized ultralow-velocity zone beneath the Marquesas Islands. These observations illustrate how approaches flexible enough to detect robust patterns with little to no user supervision can reveal distinctive insights into the deep Earth.

Extracting the main trend in a dataset: the Sequencer algorithm

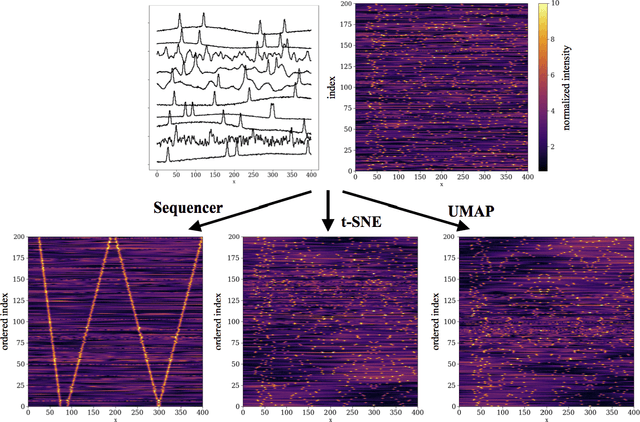
Scientists aim to extract simplicity from observations of the complex world. An important component of this process is the exploration of data in search of trends. In practice, however, this tends to be more of an art than a science. Among all trends existing in the natural world, one-dimensional trends, often called sequences, are of particular interest as they provide insights into simple phenomena. However, some are challenging to detect as they may be expressed in complex manners. We present the Sequencer, an algorithm designed to generically identify the main trend in a dataset. It does so by constructing graphs describing the similarities between pairs of observations, computed with a set of metrics and scales. Using the fact that continuous trends lead to more elongated graphs, the algorithm can identify which aspects of the data are relevant in establishing a global sequence. Such an approach can be used beyond the proposed algorithm and can optimize the parameters of any dimensionality reduction technique. We demonstrate the power of the Sequencer using real-world data from astronomy, geology as well as images from the natural world. We show that, in a number of cases, it outperforms the popular t-SNE and UMAP dimensionality reduction techniques. This approach to exploratory data analysis, which does not rely on training nor tuning of any parameter, has the potential to enable discoveries in a wide range of scientific domains. The source code is available on github and we provide an online interface at \url{http://sequencer.org}.