Feature-guided score diffusion for sampling conditional densities

Score diffusion methods can learn probability densities from samples. The score of the noise-corrupted density is estimated using a deep neural network, which is then used to iteratively transport a Gaussian white noise density to a target density. Variants for conditional densities have been developed, but correct estimation of the corresponding scores is difficult. We avoid these difficulties by introducing an algorithm that guides the diffusion with a projected score. The projection pushes the image feature vector towards the feature vector centroid of the target class. The projected score and the feature vectors are learned by the same network. Specifically, the image feature vector is defined as the spatial averages of the channels activations in select layers of the network. Optimizing the projected score for denoising loss encourages image feature vectors of each class to cluster around their centroids. It also leads to the separations of the centroids. We show that these centroids provide a low-dimensional Euclidean embedding of the class conditional densities. We demonstrate that the algorithm can generate high quality and diverse samples from the conditioning class. Conditional generation can be performed using feature vectors interpolated between those of the training set, demonstrating out-of-distribution generalization.

Hierarchic Flows to Estimate and Sample High-dimensional Probabilities

Finding low-dimensional interpretable models of complex physical fields such as turbulence remains an open question, 80 years after the pioneer work of Kolmogorov. Estimating high-dimensional probability distributions from data samples suffers from an optimization and an approximation curse of dimensionality. It may be avoided by following a hierarchic probability flow from coarse to fine scales. This inverse renormalization group is defined by conditional probabilities across scales, renormalized in a wavelet basis. For a $\varphi^4$ scalar potential, sampling these hierarchic models avoids the critical slowing down at the phase transition. An outstanding issue is to also approximate non-Gaussian fields having long-range interactions in space and across scales. We introduce low-dimensional models with robust multiscale approximations of high order polynomial energies. They are calculated with a second wavelet transform, which defines interactions over two hierarchies of scales. We estimate and sample these wavelet scattering models to generate 2D vorticity fields of turbulence, and images of dark matter densities.

Generalization in diffusion models arises from geometry-adaptive harmonic representation

High-quality samples generated with score-based reverse diffusion algorithms provide evidence that deep neural networks (DNN) trained for denoising can learn high-dimensional densities, despite the curse of dimensionality. However, recent reports of memorization of the training set raise the question of whether these networks are learning the "true" continuous density of the data. Here, we show that two denoising DNNs trained on non-overlapping subsets of a dataset learn nearly the same score function, and thus the same density, with a surprisingly small number of training images. This strong generalization demonstrates an alignment of powerful inductive biases in the DNN architecture and/or training algorithm with properties of the data distribution. We analyze these, demonstrating that the denoiser performs a shrinkage operation in a basis adapted to the underlying image. Examination of these bases reveals oscillating harmonic structures along contours and in homogeneous image regions. We show that trained denoisers are inductively biased towards these geometry-adaptive harmonic representations by demonstrating that they arise even when the network is trained on image classes such as low-dimensional manifolds, for which the harmonic basis is suboptimal. Additionally, we show that the denoising performance of the networks is near-optimal when trained on regular image classes for which the optimal basis is known to be geometry-adaptive and harmonic.

Scattering Spectra Models for Physics

Physicists routinely need probabilistic models for a number of tasks such as parameter inference or the generation of new realizations of a field. Establishing such models for highly non-Gaussian fields is a challenge, especially when the number of samples is limited. In this paper, we introduce scattering spectra models for stationary fields and we show that they provide accurate and robust statistical descriptions of a wide range of fields encountered in physics. These models are based on covariances of scattering coefficients, i.e. wavelet decomposition of a field coupled with a point-wise modulus. After introducing useful dimension reductions taking advantage of the regularity of a field under rotation and scaling, we validate these models on various multi-scale physical fields and demonstrate that they reproduce standard statistics, including spatial moments up to 4th order. These scattering spectra provide us with a low-dimensional structured representation that captures key properties encountered in a wide range of physical fields. These generic models can be used for data exploration, classification, parameter inference, symmetry detection, and component separation.

Conditionally Strongly Log-Concave Generative Models

There is a growing gap between the impressive results of deep image generative models and classical algorithms that offer theoretical guarantees. The former suffer from mode collapse or memorization issues, limiting their application to scientific data. The latter require restrictive assumptions such as log-concavity to escape the curse of dimensionality. We partially bridge this gap by introducing conditionally strongly log-concave (CSLC) models, which factorize the data distribution into a product of conditional probability distributions that are strongly log-concave. This factorization is obtained with orthogonal projectors adapted to the data distribution. It leads to efficient parameter estimation and sampling algorithms, with theoretical guarantees, although the data distribution is not globally log-concave. We show that several challenging multiscale processes are conditionally log-concave using wavelet packet orthogonal projectors. Numerical results are shown for physical fields such as the $\varphi^4$ model and weak lensing convergence maps with higher resolution than in previous works.

A Rainbow in Deep Network Black Boxes

We introduce rainbow networks as a probabilistic model of trained deep neural networks. The model cascades random feature maps whose weight distributions are learned. It assumes that dependencies between weights at different layers are reduced to rotations which align the input activations. Neuron weights within a layer are independent after this alignment. Their activations define kernels which become deterministic in the infinite-width limit. This is verified numerically for ResNets trained on the ImageNet dataset. We also show that the learned weight distributions have low-rank covariances. Rainbow networks thus alternate between linear dimension reductions and non-linear high-dimensional embeddings with white random features. Gaussian rainbow networks are defined with Gaussian weight distributions. These models are validated numerically on image classification on the CIFAR-10 dataset, with wavelet scattering networks. We further show that during training, SGD updates the weight covariances while mostly preserving the Gaussian initialization.

Learning multi-scale local conditional probability models of images

Deep neural networks can learn powerful prior probability models for images, as evidenced by the high-quality generations obtained with recent score-based diffusion methods. But the means by which these networks capture complex global statistical structure, apparently without suffering from the curse of dimensionality, remain a mystery. To study this, we incorporate diffusion methods into a multi-scale decomposition, reducing dimensionality by assuming a stationary local Markov model for wavelet coefficients conditioned on coarser-scale coefficients. We instantiate this model using convolutional neural networks (CNNs) with local receptive fields, which enforce both the stationarity and Markov properties. Global structures are captured using a CNN with receptive fields covering the entire (but small) low-pass image. We test this model on a dataset of face images, which are highly non-stationary and contain large-scale geometric structures. Remarkably, denoising, super-resolution, and image synthesis results all demonstrate that these structures can be captured with significantly smaller conditioning neighborhoods than required by a Markov model implemented in the pixel domain. Our results show that score estimation for large complex images can be reduced to low-dimensional Markov conditional models across scales, alleviating the curse of dimensionality.

Wavelet Conditional Renormalization Group

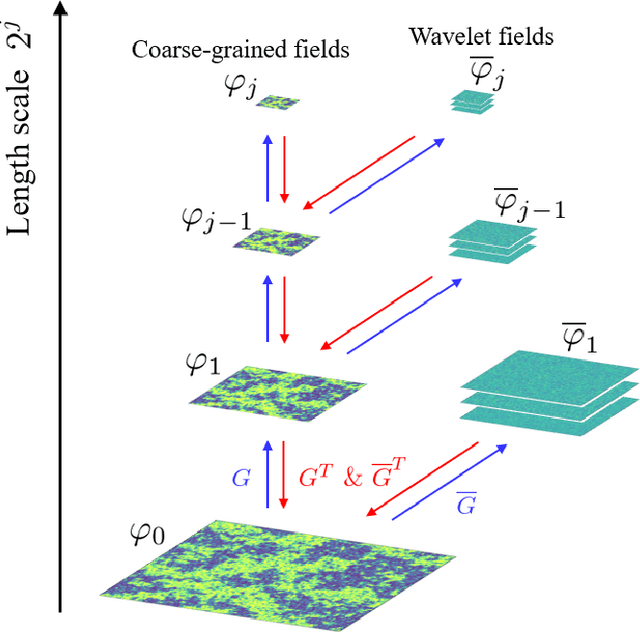
We develop a multiscale approach to estimate high-dimensional probability distributions from a dataset of physical fields or configurations observed in experiments or simulations. In this way we can estimate energy functions (or Hamiltonians) and efficiently generate new samples of many-body systems in various domains, from statistical physics to cosmology. Our method -- the Wavelet Conditional Renormalization Group (WC-RG) -- proceeds scale by scale, estimating models for the conditional probabilities of "fast degrees of freedom" conditioned by coarse-grained fields. These probability distributions are modeled by energy functions associated with scale interactions, and are represented in an orthogonal wavelet basis. WC-RG decomposes the microscopic energy function as a sum of interaction energies at all scales and can efficiently generate new samples by going from coarse to fine scales. Near phase transitions, it avoids the "critical slowing down" of direct estimation and sampling algorithms. This is explained theoretically by combining results from RG and wavelet theories, and verified numerically for the Gaussian and $\varphi^4$ field theories. We show that multiscale WC-RG energy-based models are more general than local potential models and can capture the physics of complex many-body interacting systems at all length scales. This is demonstrated for weak-gravitational-lensing fields reflecting dark matter distributions in cosmology, which include long-range interactions with long-tail probability distributions. WC-RG has a large number of potential applications in non-equilibrium systems, where the underlying distribution is not known {\it a priori}. Finally, we discuss the connection between WC-RG and deep network architectures.

Scale Dependencies and Self-Similarity Through Wavelet Scattering Covariance

We introduce a scattering covariance matrix which provides non-Gaussian models of time-series having stationary increments. A complex wavelet transform computes signal variations at each scale. Dependencies across scales are captured by the joint covariance across time and scales of complex wavelet coefficients and their modulus. This covariance is nearly diagonalized by a second wavelet transform, which defines the scattering covariance. We show that this set of moments characterizes a wide range of non-Gaussian properties of multi-scale processes. This is analyzed for a variety of processes, including fractional Brownian motions, Poisson, multifractal random walks and Hawkes processes. We prove that self-similar processes have a scattering covariance matrix which is scale invariant. This property can be estimated numerically and defines a class of wide-sense self-similar processes. We build maximum entropy models conditioned by scattering covariance coefficients, and generate new time-series with a microcanonical sampling algorithm. Applications are shown for highly non-Gaussian financial and turbulence time-series.

Generalized Rectifier Wavelet Covariance Models For Texture Synthesis

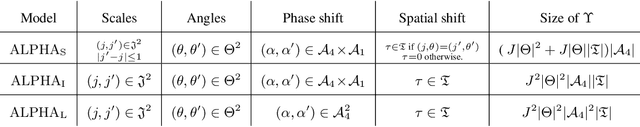
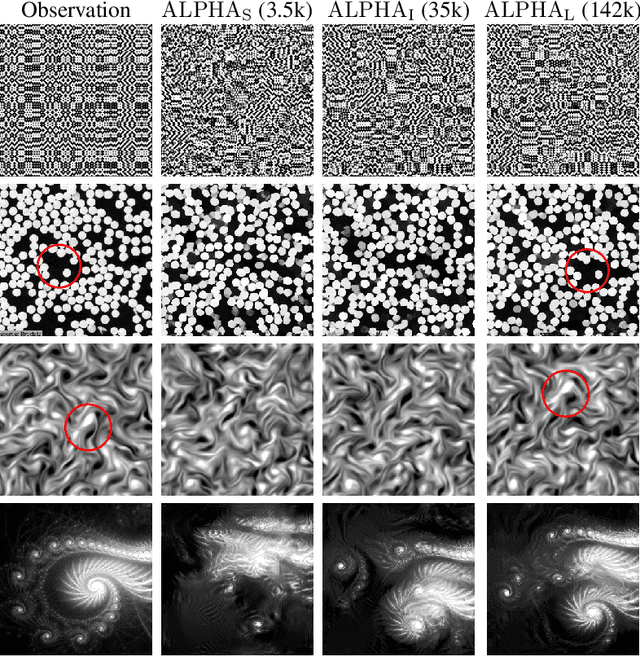
State-of-the-art maximum entropy models for texture synthesis are built from statistics relying on image representations defined by convolutional neural networks (CNN). Such representations capture rich structures in texture images, outperforming wavelet-based representations in this regard. However, conversely to neural networks, wavelets offer meaningful representations, as they are known to detect structures at multiple scales (e.g. edges) in images. In this work, we propose a family of statistics built upon non-linear wavelet based representations, that can be viewed as a particular instance of a one-layer CNN, using a generalized rectifier non-linearity. These statistics significantly improve the visual quality of previous classical wavelet-based models, and allow one to produce syntheses of similar quality to state-of-the-art models, on both gray-scale and color textures.