Learning a Maximum Entropy Model for Visual Textures using Diffusion

Visual textures -- spatially homogeneous image regions containing repeated elements (e.g. a field of grass, the bark of a tree) -- are ubiquitous in visual scenes and provide important cues for recognizing and analyzing materials and objects. A number of existing texture models extract essential statistics from a single texture image, and can then generate high-quality samples that are visually similar to the original by matching these statistics. However, their statistics are either hand-designed or based on a network pretrained for another purpose (e.g., object recognition). Here, we develop the first principled method for unsupervised learning of a set of statistics that are used to constrain a maximum entropy probability model. We leverage methods developed for generative diffusion models to derive training and sampling procedures, and compare these to the traditional method of sampling via matching the statistics. Despite the compactness of our trained model (512 statistics), it generates texture images whose quality is as good as or better than the current state-of-the-art model (~177k statistics). A more direct comparison of the two models, obtained by synthesizing images that are indistinguishable for one model but maximally different for the other, reveals their relative strengths and weaknesses. Finally, we show that unlike previous statistical texture models, a straight trajectory in the representation space of our model generates homogeneous texture samples that interpolate smoothly between the features of the two end points.

Disentangled representations via score-based variational autoencoders

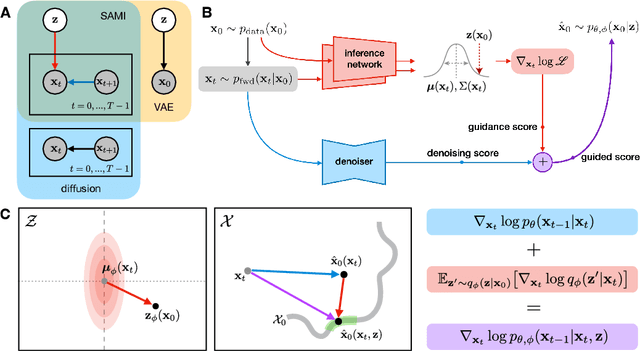
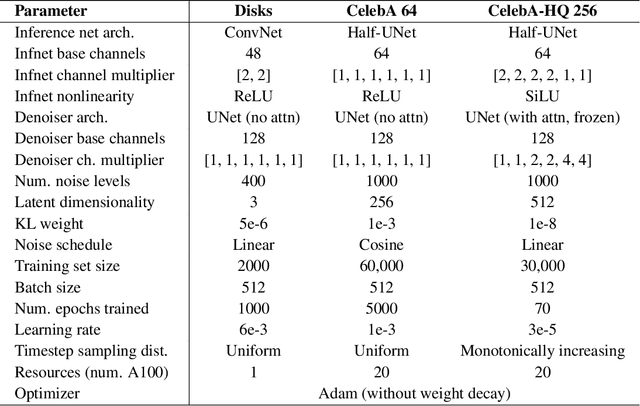
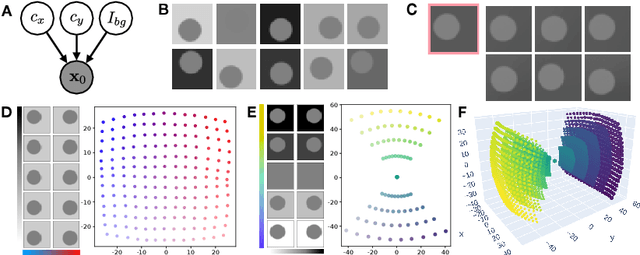
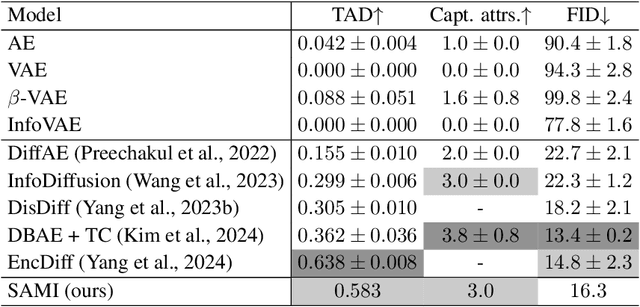
We present the Score-based Autoencoder for Multiscale Inference (SAMI), a method for unsupervised representation learning that combines the theoretical frameworks of diffusion models and VAEs. By unifying their respective evidence lower bounds, SAMI formulates a principled objective that learns representations through score-based guidance of the underlying diffusion process. The resulting representations automatically capture meaningful structure in the data: it recovers ground truth generative factors in our synthetic dataset, learns factorized, semantic latent dimensions from complex natural images, and encodes video sequences into latent trajectories that are straighter than those of alternative encoders, despite training exclusively on static images. Furthermore, SAMI can extract useful representations from pre-trained diffusion models with minimal additional training. Finally, the explicitly probabilistic formulation provides new ways to identify semantically meaningful axes in the absence of supervised labels, and its mathematical exactness allows us to make formal statements about the nature of the learned representation. Overall, these results indicate that implicit structural information in diffusion models can be made explicit and interpretable through synergistic combination with a variational autoencoder.

Learning predictable and robust neural representations by straightening image sequences

Prediction is a fundamental capability of all living organisms, and has been proposed as an objective for learning sensory representations. Recent work demonstrates that in primate visual systems, prediction is facilitated by neural representations that follow straighter temporal trajectories than their initial photoreceptor encoding, which allows for prediction by linear extrapolation. Inspired by these experimental findings, we develop a self-supervised learning (SSL) objective that explicitly quantifies and promotes straightening. We demonstrate the power of this objective in training deep feedforward neural networks on smoothly-rendered synthetic image sequences that mimic commonly-occurring properties of natural videos. The learned model contains neural embeddings that are predictive, but also factorize the geometric, photometric, and semantic attributes of objects. The representations also prove more robust to noise and adversarial attacks compared to previous SSL methods that optimize for invariance to random augmentations. Moreover, these beneficial properties can be transferred to other training procedures by using the straightening objective as a regularizer, suggesting a broader utility for straightening as a principle for robust unsupervised learning.

Video prediction using score-based conditional density estimation

Temporal prediction is inherently uncertain, but representing the ambiguity in natural image sequences is a challenging high-dimensional probabilistic inference problem. For natural scenes, the curse of dimensionality renders explicit density estimation statistically and computationally intractable. Here, we describe an implicit regression-based framework for learning and sampling the conditional density of the next frame in a video given previous observed frames. We show that sequence-to-image deep networks trained on a simple resilience-to-noise objective function extract adaptive representations for temporal prediction. Synthetic experiments demonstrate that this score-based framework can handle occlusion boundaries: unlike classical methods that average over bifurcating temporal trajectories, it chooses among likely trajectories, selecting more probable options with higher frequency. Furthermore, analysis of networks trained on natural image sequences reveals that the representation automatically weights predictive evidence by its reliability, which is a hallmark of statistical inference

Discriminating image representations with principal distortions

Image representations (artificial or biological) are often compared in terms of their global geometry; however, representations with similar global structure can have strikingly different local geometries. Here, we propose a framework for comparing a set of image representations in terms of their local geometries. We quantify the local geometry of a representation using the Fisher information matrix, a standard statistical tool for characterizing the sensitivity to local stimulus distortions, and use this as a substrate for a metric on the local geometry in the vicinity of a base image. This metric may then be used to optimally differentiate a set of models, by finding a pair of "principal distortions" that maximize the variance of the models under this metric. We use this framework to compare a set of simple models of the early visual system, identifying a novel set of image distortions that allow immediate comparison of the models by visual inspection. In a second example, we apply our method to a set of deep neural network models and reveal differences in the local geometry that arise due to architecture and training types. These examples highlight how our framework can be used to probe for informative differences in local sensitivities between complex computational models, and suggest how it could be used to compare model representations with human perception.

Feature-guided score diffusion for sampling conditional densities

Score diffusion methods can learn probability densities from samples. The score of the noise-corrupted density is estimated using a deep neural network, which is then used to iteratively transport a Gaussian white noise density to a target density. Variants for conditional densities have been developed, but correct estimation of the corresponding scores is difficult. We avoid these difficulties by introducing an algorithm that guides the diffusion with a projected score. The projection pushes the image feature vector towards the feature vector centroid of the target class. The projected score and the feature vectors are learned by the same network. Specifically, the image feature vector is defined as the spatial averages of the channels activations in select layers of the network. Optimizing the projected score for denoising loss encourages image feature vectors of each class to cluster around their centroids. It also leads to the separations of the centroids. We show that these centroids provide a low-dimensional Euclidean embedding of the class conditional densities. We demonstrate that the algorithm can generate high quality and diverse samples from the conditioning class. Conditional generation can be performed using feature vectors interpolated between those of the training set, demonstrating out-of-distribution generalization.

Optimized Linear Measurements for Inverse Problems using Diffusion-Based Image Generation

We re-examine the problem of reconstructing a high-dimensional signal from a small set of linear measurements, in combination with image prior from a diffusion probabilistic model. Well-established methods for optimizing such measurements include principal component analysis (PCA), independent component analysis (ICA) and compressed sensing (CS), all of which rely on axis- or subspace-aligned statistical characterization. But many naturally occurring signals, including photographic images, contain richer statistical structure. To exploit such structure, we introduce a general method for obtaining an optimized set of linear measurements, assuming a Bayesian inverse solution that leverages the prior implicit in a neural network trained to perform denoising. We demonstrate that these measurements are distinct from those of PCA and CS, with significant improvements in minimizing squared reconstruction error. In addition, we show that optimizing the measurements for the SSIM perceptual loss leads to perceptually improved reconstruction. Our results highlight the importance of incorporating the specific statistical regularities of natural signals when designing effective linear measurements.

Layerwise complexity-matched learning yields an improved model of cortical area V2

Human ability to recognize complex visual patterns arises through transformations performed by successive areas in the ventral visual cortex. Deep neural networks trained end-to-end for object recognition approach human capabilities, and offer the best descriptions to date of neural responses in the late stages of the hierarchy. But these networks provide a poor account of the early stages, compared to traditional hand-engineered models, or models optimized for coding efficiency or prediction. Moreover, the gradient backpropagation used in end-to-end learning is generally considered to be biologically implausible. Here, we overcome both of these limitations by developing a bottom-up self-supervised training methodology that operates independently on successive layers. Specifically, we maximize feature similarity between pairs of locally-deformed natural image patches, while decorrelating features across patches sampled from other images. Crucially, the deformation amplitudes are adjusted proportionally to receptive field sizes in each layer, thus matching the task complexity to the capacity at each stage of processing. In comparison with architecture-matched versions of previous models, we demonstrate that our layerwise complexity-matched learning (LCL) formulation produces a two-stage model (LCL-V2) that is better aligned with selectivity properties and neural activity in primate area V2. We demonstrate that the complexity-matched learning paradigm is critical for the emergence of the improved biological alignment. Finally, when the two-stage model is used as a fixed front-end for a deep network trained to perform object recognition, the resultant model (LCL-V2Net) is significantly better than standard end-to-end self-supervised, supervised, and adversarially-trained models in terms of generalization to out-of-distribution tasks and alignment with human behavior.

Generalization in diffusion models arises from geometry-adaptive harmonic representation

High-quality samples generated with score-based reverse diffusion algorithms provide evidence that deep neural networks (DNN) trained for denoising can learn high-dimensional densities, despite the curse of dimensionality. However, recent reports of memorization of the training set raise the question of whether these networks are learning the "true" continuous density of the data. Here, we show that two denoising DNNs trained on non-overlapping subsets of a dataset learn nearly the same score function, and thus the same density, with a surprisingly small number of training images. This strong generalization demonstrates an alignment of powerful inductive biases in the DNN architecture and/or training algorithm with properties of the data distribution. We analyze these, demonstrating that the denoiser performs a shrinkage operation in a basis adapted to the underlying image. Examination of these bases reveals oscillating harmonic structures along contours and in homogeneous image regions. We show that trained denoisers are inductively biased towards these geometry-adaptive harmonic representations by demonstrating that they arise even when the network is trained on image classes such as low-dimensional manifolds, for which the harmonic basis is suboptimal. Additionally, we show that the denoising performance of the networks is near-optimal when trained on regular image classes for which the optimal basis is known to be geometry-adaptive and harmonic.

Adaptive whitening with fast gain modulation and slow synaptic plasticity

Neurons in early sensory areas rapidly adapt to changing sensory statistics, both by normalizing the variance of their individual responses and by reducing correlations between their responses. Together, these transformations may be viewed as an adaptive form of statistical whitening. Existing mechanistic models of adaptive whitening exclusively use either synaptic plasticity or gain modulation as the biological substrate for adaptation; however, on their own, each of these models has significant limitations. In this work, we unify these approaches in a normative multi-timescale mechanistic model that adaptively whitens its responses with complementary computational roles for synaptic plasticity and gain modulation. Gains are modified on a fast timescale to adapt to the current statistical context, whereas synapses are modified on a slow timescale to learn structural properties of the input statistics that are invariant across contexts. Our model is derived from a novel multi-timescale whitening objective that factorizes the inverse whitening matrix into basis vectors, which correspond to synaptic weights, and a diagonal matrix, which corresponds to neuronal gains. We test our model on synthetic and natural datasets and find that the synapses learn optimal configurations over long timescales that enable the circuit to adaptively whiten neural responses on short timescales exclusively using gain modulation.