Classification-Denoising Networks

Image classification and denoising suffer from complementary issues of lack of robustness or partially ignoring conditioning information. We argue that they can be alleviated by unifying both tasks through a model of the joint probability of (noisy) images and class labels. Classification is performed with a forward pass followed by conditioning. Using the Tweedie-Miyasawa formula, we evaluate the denoising function with the score, which can be computed by marginalization and back-propagation. The training objective is then a combination of cross-entropy loss and denoising score matching loss integrated over noise levels. Numerical experiments on CIFAR-10 and ImageNet show competitive classification and denoising performance compared to reference deep convolutional classifiers/denoisers, and significantly improves efficiency compared to previous joint approaches. Our model shows an increased robustness to adversarial perturbations compared to a standard discriminative classifier, and allows for a novel interpretation of adversarial gradients as a difference of denoisers.

On the universality of neural encodings in CNNs

We explore the universality of neural encodings in convolutional neural networks trained on image classification tasks. We develop a procedure to directly compare the learned weights rather than their representations. It is based on a factorization of spatial and channel dimensions and measures the similarity of aligned weight covariances. We show that, for a range of layers of VGG-type networks, the learned eigenvectors appear to be universal across different natural image datasets. Our results suggest the existence of a universal neural encoding for natural images. They explain, at a more fundamental level, the success of transfer learning. Our work shows that, instead of aiming at maximizing the performance of neural networks, one can alternatively attempt to maximize the universality of the learned encoding, in order to build a principled foundation model.

Generalization in diffusion models arises from geometry-adaptive harmonic representation

High-quality samples generated with score-based reverse diffusion algorithms provide evidence that deep neural networks (DNN) trained for denoising can learn high-dimensional densities, despite the curse of dimensionality. However, recent reports of memorization of the training set raise the question of whether these networks are learning the "true" continuous density of the data. Here, we show that two denoising DNNs trained on non-overlapping subsets of a dataset learn nearly the same score function, and thus the same density, with a surprisingly small number of training images. This strong generalization demonstrates an alignment of powerful inductive biases in the DNN architecture and/or training algorithm with properties of the data distribution. We analyze these, demonstrating that the denoiser performs a shrinkage operation in a basis adapted to the underlying image. Examination of these bases reveals oscillating harmonic structures along contours and in homogeneous image regions. We show that trained denoisers are inductively biased towards these geometry-adaptive harmonic representations by demonstrating that they arise even when the network is trained on image classes such as low-dimensional manifolds, for which the harmonic basis is suboptimal. Additionally, we show that the denoising performance of the networks is near-optimal when trained on regular image classes for which the optimal basis is known to be geometry-adaptive and harmonic.

Conditionally Strongly Log-Concave Generative Models

There is a growing gap between the impressive results of deep image generative models and classical algorithms that offer theoretical guarantees. The former suffer from mode collapse or memorization issues, limiting their application to scientific data. The latter require restrictive assumptions such as log-concavity to escape the curse of dimensionality. We partially bridge this gap by introducing conditionally strongly log-concave (CSLC) models, which factorize the data distribution into a product of conditional probability distributions that are strongly log-concave. This factorization is obtained with orthogonal projectors adapted to the data distribution. It leads to efficient parameter estimation and sampling algorithms, with theoretical guarantees, although the data distribution is not globally log-concave. We show that several challenging multiscale processes are conditionally log-concave using wavelet packet orthogonal projectors. Numerical results are shown for physical fields such as the $\varphi^4$ model and weak lensing convergence maps with higher resolution than in previous works.

A Rainbow in Deep Network Black Boxes

We introduce rainbow networks as a probabilistic model of trained deep neural networks. The model cascades random feature maps whose weight distributions are learned. It assumes that dependencies between weights at different layers are reduced to rotations which align the input activations. Neuron weights within a layer are independent after this alignment. Their activations define kernels which become deterministic in the infinite-width limit. This is verified numerically for ResNets trained on the ImageNet dataset. We also show that the learned weight distributions have low-rank covariances. Rainbow networks thus alternate between linear dimension reductions and non-linear high-dimensional embeddings with white random features. Gaussian rainbow networks are defined with Gaussian weight distributions. These models are validated numerically on image classification on the CIFAR-10 dataset, with wavelet scattering networks. We further show that during training, SGD updates the weight covariances while mostly preserving the Gaussian initialization.

Learning multi-scale local conditional probability models of images

Deep neural networks can learn powerful prior probability models for images, as evidenced by the high-quality generations obtained with recent score-based diffusion methods. But the means by which these networks capture complex global statistical structure, apparently without suffering from the curse of dimensionality, remain a mystery. To study this, we incorporate diffusion methods into a multi-scale decomposition, reducing dimensionality by assuming a stationary local Markov model for wavelet coefficients conditioned on coarser-scale coefficients. We instantiate this model using convolutional neural networks (CNNs) with local receptive fields, which enforce both the stationarity and Markov properties. Global structures are captured using a CNN with receptive fields covering the entire (but small) low-pass image. We test this model on a dataset of face images, which are highly non-stationary and contain large-scale geometric structures. Remarkably, denoising, super-resolution, and image synthesis results all demonstrate that these structures can be captured with significantly smaller conditioning neighborhoods than required by a Markov model implemented in the pixel domain. Our results show that score estimation for large complex images can be reduced to low-dimensional Markov conditional models across scales, alleviating the curse of dimensionality.

Wavelet Score-Based Generative Modeling

Score-based generative models (SGMs) synthesize new data samples from Gaussian white noise by running a time-reversed Stochastic Differential Equation (SDE) whose drift coefficient depends on some probabilistic score. The discretization of such SDEs typically requires a large number of time steps and hence a high computational cost. This is because of ill-conditioning properties of the score that we analyze mathematically. We show that SGMs can be considerably accelerated, by factorizing the data distribution into a product of conditional probabilities of wavelet coefficients across scales. The resulting Wavelet Score-based Generative Model (WSGM) synthesizes wavelet coefficients with the same number of time steps at all scales, and its time complexity therefore grows linearly with the image size. This is proved mathematically over Gaussian distributions, and shown numerically over physical processes at phase transition and natural image datasets.

Phase Collapse in Neural Networks

Deep convolutional image classifiers progressively transform the spatial variability into a smaller number of channels, which linearly separates all classes. A fundamental challenge is to understand the role of rectifiers together with convolutional filters in this transformation. Rectifiers with biases are often interpreted as thresholding operators which improve sparsity and discrimination. This paper demonstrates that it is a different phase collapse mechanism which explains the ability to progressively eliminate spatial variability, while improving linear class separation. This is explained and shown numerically by defining a simplified complex-valued convolutional network architecture. It implements spatial convolutions with wavelet filters and uses a complex modulus to collapse phase variables. This phase collapse network reaches the classification accuracy of ResNets of similar depths, whereas its performance is considerably degraded when replacing the phase collapse with thresholding operators. This is justified by explaining how iterated phase collapses progressively improve separation of class means, as opposed to thresholding non-linearities.

Separation and Concentration in Deep Networks

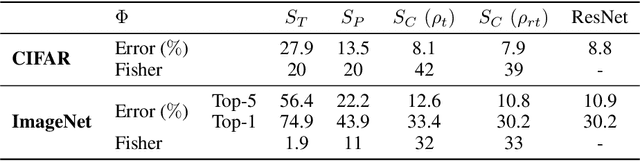
Numerical experiments demonstrate that deep neural network classifiers progressively separate class distributions around their mean, achieving linear separability on the training set, and increasing the Fisher discriminant ratio. We explain this mechanism with two types of operators. We prove that a rectifier without biases applied to sign-invariant tight frames can separate class means and increase Fisher ratios. On the opposite, a soft-thresholding on tight frames can reduce within-class variabilities while preserving class means. Variance reduction bounds are proved for Gaussian mixture models. For image classification, we show that separation of class means can be achieved with rectified wavelet tight frames that are not learned. It defines a scattering transform. Learning $1 \times 1$ convolutional tight frames along scattering channels and applying a soft-thresholding reduces within-class variabilities. The resulting scattering network reaches the classification accuracy of ResNet-18 on CIFAR-10 and ImageNet, with fewer layers and no learned biases.