Separation and Concentration in Deep Networks
Paper and Code
Dec 18, 2020

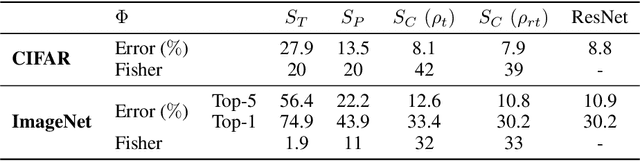

Numerical experiments demonstrate that deep neural network classifiers progressively separate class distributions around their mean, achieving linear separability on the training set, and increasing the Fisher discriminant ratio. We explain this mechanism with two types of operators. We prove that a rectifier without biases applied to sign-invariant tight frames can separate class means and increase Fisher ratios. On the opposite, a soft-thresholding on tight frames can reduce within-class variabilities while preserving class means. Variance reduction bounds are proved for Gaussian mixture models. For image classification, we show that separation of class means can be achieved with rectified wavelet tight frames that are not learned. It defines a scattering transform. Learning $1 \times 1$ convolutional tight frames along scattering channels and applying a soft-thresholding reduces within-class variabilities. The resulting scattering network reaches the classification accuracy of ResNet-18 on CIFAR-10 and ImageNet, with fewer layers and no learned biases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge