Discriminating image representations with principal distortions

Image representations (artificial or biological) are often compared in terms of their global geometry; however, representations with similar global structure can have strikingly different local geometries. Here, we propose a framework for comparing a set of image representations in terms of their local geometries. We quantify the local geometry of a representation using the Fisher information matrix, a standard statistical tool for characterizing the sensitivity to local stimulus distortions, and use this as a substrate for a metric on the local geometry in the vicinity of a base image. This metric may then be used to optimally differentiate a set of models, by finding a pair of "principal distortions" that maximize the variance of the models under this metric. We use this framework to compare a set of simple models of the early visual system, identifying a novel set of image distortions that allow immediate comparison of the models by visual inspection. In a second example, we apply our method to a set of deep neural network models and reveal differences in the local geometry that arise due to architecture and training types. These examples highlight how our framework can be used to probe for informative differences in local sensitivities between complex computational models, and suggest how it could be used to compare model representations with human perception.

A Spectral Theory of Neural Prediction and Alignment

The representations of neural networks are often compared to those of biological systems by performing regression between the neural network responses and those measured from biological systems. Many different state-of-the-art deep neural networks yield similar neural predictions, but it remains unclear how to differentiate among models that perform equally well at predicting neural responses. To gain insight into this, we use a recent theoretical framework that relates the generalization error from regression to the spectral bias of the model activations and the alignment of the neural responses onto the learnable subspace of the model. We extend this theory to the case of regression between model activations and neural responses, and define geometrical properties describing the error embedding geometry. We test a large number of deep neural networks that predict visual cortical activity and show that there are multiple types of geometries that result in low neural prediction error as measured via regression. The work demonstrates that carefully decomposing representational metrics can provide interpretability of how models are capturing neural activity and points the way towards improved models of neural activity.

Neural Population Geometry Reveals the Role of Stochasticity in Robust Perception

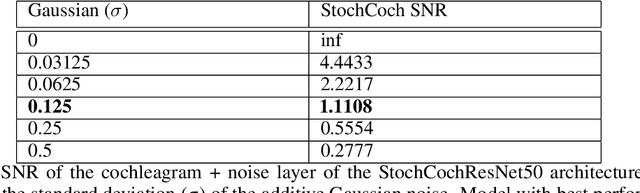
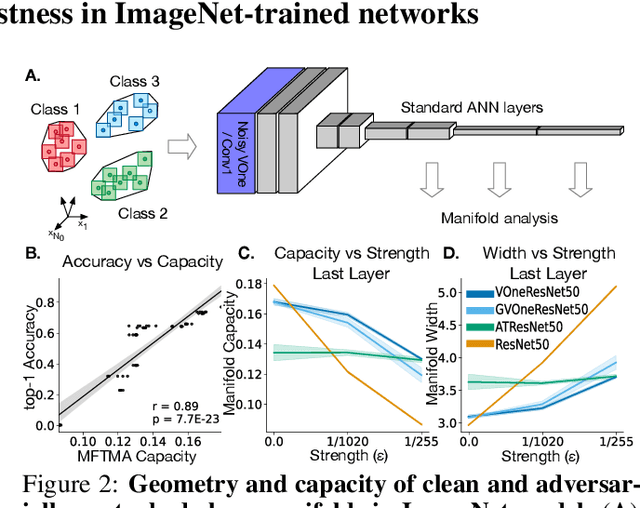
Adversarial examples are often cited by neuroscientists and machine learning researchers as an example of how computational models diverge from biological sensory systems. Recent work has proposed adding biologically-inspired components to visual neural networks as a way to improve their adversarial robustness. One surprisingly effective component for reducing adversarial vulnerability is response stochasticity, like that exhibited by biological neurons. Here, using recently developed geometrical techniques from computational neuroscience, we investigate how adversarial perturbations influence the internal representations of standard, adversarially trained, and biologically-inspired stochastic networks. We find distinct geometric signatures for each type of network, revealing different mechanisms for achieving robust representations. Next, we generalize these results to the auditory domain, showing that neural stochasticity also makes auditory models more robust to adversarial perturbations. Geometric analysis of the stochastic networks reveals overlap between representations of clean and adversarially perturbed stimuli, and quantitatively demonstrates that competing geometric effects of stochasticity mediate a tradeoff between adversarial and clean performance. Our results shed light on the strategies of robust perception utilized by adversarially trained and stochastic networks, and help explain how stochasticity may be beneficial to machine and biological computation.

Untangling in Invariant Speech Recognition

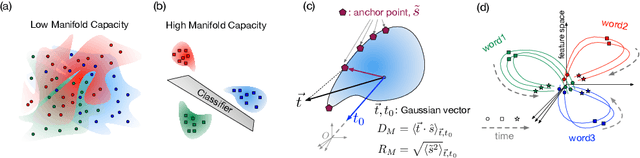
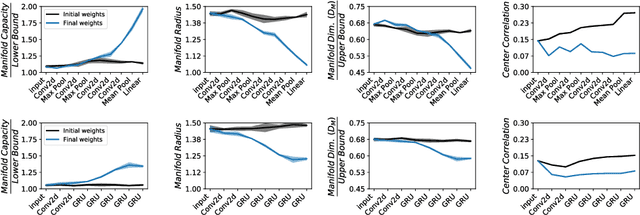
Encouraged by the success of deep neural networks on a variety of visual tasks, much theoretical and experimental work has been aimed at understanding and interpreting how vision networks operate. Meanwhile, deep neural networks have also achieved impressive performance in audio processing applications, both as sub-components of larger systems and as complete end-to-end systems by themselves. Despite their empirical successes, comparatively little is understood about how these audio models accomplish these tasks. In this work, we employ a recently developed statistical mechanical theory that connects geometric properties of network representations and the separability of classes to probe how information is untangled within neural networks trained to recognize speech. We observe that speaker-specific nuisance variations are discarded by the network's hierarchy, whereas task-relevant properties such as words and phonemes are untangled in later layers. Higher level concepts such as parts-of-speech and context dependence also emerge in the later layers of the network. Finally, we find that the deep representations carry out significant temporal untangling by efficiently extracting task-relevant features at each time step of the computation. Taken together, these findings shed light on how deep auditory models process time dependent input signals to achieve invariant speech recognition, and show how different concepts emerge through the layers of the network.