Spectral Analysis of Representational Similarity with Limited Neurons

Measuring representational similarity between neural recordings and computational models is challenging due to constraints on the number of neurons that can be recorded simultaneously. In this work, we investigate how such limitations affect similarity measures, focusing on Canonical Correlation Analysis (CCA) and Centered Kernel Alignment (CKA). Leveraging tools from Random Matrix Theory, we develop a predictive spectral framework for these measures and demonstrate that finite neuron sampling systematically underestimates similarity due to eigenvector delocalization. To overcome this, we introduce a denoising method to infer population-level similarity, enabling accurate analysis even with small neuron samples. Our theory is validated on synthetic and real datasets, offering practical strategies for interpreting neural data under finite sampling constraints.

Estimating Neural Representation Alignment from Limited Inputs and Features

In both artificial and biological systems, the centered kernel alignment (CKA) has become a widely used tool for quantifying neural representation similarity. While current CKA estimators typically correct for the effects of finite stimuli sampling, the effects of sampling a subset of neurons are overlooked, introducing notable bias in standard experimental scenarios. Here, we provide a theoretical analysis showing how this bias is affected by the representation geometry. We then introduce a novel estimator that corrects for both input and feature sampling. We use our method for evaluating both brain-to-brain and model-to-brain alignments and show that it delivers reliable comparisons even with very sparsely sampled neurons. We perform within-animal and across-animal comparisons on electrophysiological data from visual cortical areas V1, V4, and IT data, and use these as benchmarks to evaluate model-to-brain alignment. We also apply our method to reveal how object representations become progressively disentangled across layers in both biological and artificial systems. These findings underscore the importance of correcting feature-sampling biases in CKA and demonstrate that our bias-corrected estimator provides a more faithful measure of representation alignment. The improved estimates increase our understanding of how neural activity is structured across both biological and artificial systems.

Statistical Mechanics of Support Vector Regression

A key problem in deep learning and computational neuroscience is relating the geometrical properties of neural representations to task performance. Here, we consider this problem for continuous decoding tasks where neural variability may affect task precision. Using methods from statistical mechanics, we study the average-case learning curves for $\varepsilon$-insensitive Support Vector Regression ($\varepsilon$-SVR) and discuss its capacity as a measure of linear decodability. Our analysis reveals a phase transition in the training error at a critical load, capturing the interplay between the tolerance parameter $\varepsilon$ and neural variability. We uncover a double-descent phenomenon in the generalization error, showing that $\varepsilon$ acts as a regularizer, both suppressing and shifting these peaks. Theoretical predictions are validated both on toy models and deep neural networks, extending the theory of Support Vector Machines to continuous tasks with inherent neural variability.

A Spectral Theory of Neural Prediction and Alignment

The representations of neural networks are often compared to those of biological systems by performing regression between the neural network responses and those measured from biological systems. Many different state-of-the-art deep neural networks yield similar neural predictions, but it remains unclear how to differentiate among models that perform equally well at predicting neural responses. To gain insight into this, we use a recent theoretical framework that relates the generalization error from regression to the spectral bias of the model activations and the alignment of the neural responses onto the learnable subspace of the model. We extend this theory to the case of regression between model activations and neural responses, and define geometrical properties describing the error embedding geometry. We test a large number of deep neural networks that predict visual cortical activity and show that there are multiple types of geometries that result in low neural prediction error as measured via regression. The work demonstrates that carefully decomposing representational metrics can provide interpretability of how models are capturing neural activity and points the way towards improved models of neural activity.

Bandwidth Enables Generalization in Quantum Kernel Models

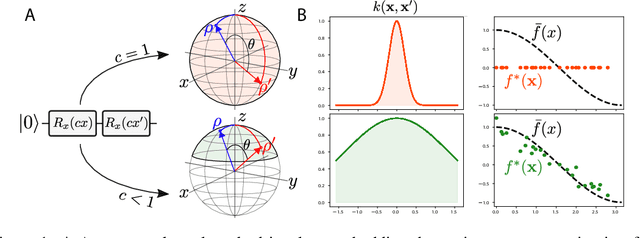
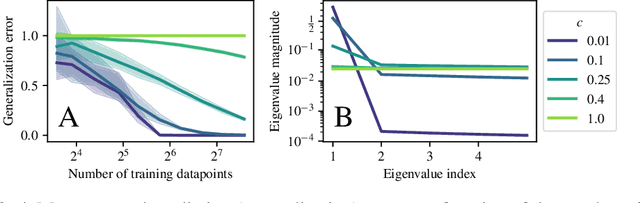
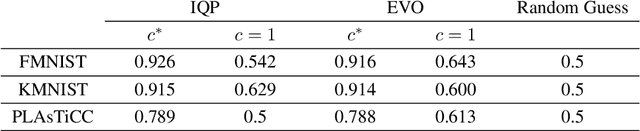
Quantum computers are known to provide speedups over classical state-of-the-art machine learning methods in some specialized settings. For example, quantum kernel methods have been shown to provide an exponential speedup on a learning version of the discrete logarithm problem. Understanding the generalization of quantum models is essential to realizing similar speedups on problems of practical interest. Recent results demonstrate that generalization is hindered by the exponential size of the quantum feature space. Although these results suggest that quantum models cannot generalize when the number of qubits is large, in this paper we show that these results rely on overly restrictive assumptions. We consider a wider class of models by varying a hyperparameter that we call quantum kernel bandwidth. We analyze the large-qubit limit and provide explicit formulas for the generalization of a quantum model that can be solved in closed form. Specifically, we show that changing the value of the bandwidth can take a model from provably not being able to generalize to any target function to good generalization for well-aligned targets. Our analysis shows how the bandwidth controls the spectrum of the kernel integral operator and thereby the inductive bias of the model. We demonstrate empirically that our theory correctly predicts how varying the bandwidth affects generalization of quantum models on challenging datasets, including those far outside our theoretical assumptions. We discuss the implications of our results for quantum advantage in machine learning.

Asymptotics of representation learning in finite Bayesian neural networks

Recent works have suggested that finite Bayesian neural networks may outperform their infinite cousins because finite networks can flexibly adapt their internal representations. However, our theoretical understanding of how the learned hidden layer representations of finite networks differ from the fixed representations of infinite networks remains incomplete. Perturbative finite-width corrections to the network prior and posterior have been studied, but the asymptotics of learned features have not been fully characterized. Here, we argue that the leading finite-width corrections to the average feature kernels for any Bayesian network with linear readout and quadratic cost have a largely universal form. We illustrate this explicitly for two classes of fully connected networks: deep linear networks and networks with a single nonlinear hidden layer. Our results begin to elucidate which features of data wide Bayesian neural networks learn to represent.

Out-of-Distribution Generalization in Kernel Regression

In real word applications, data generating process for training a machine learning model often differs from what the model encounters in the test stage. Understanding how and whether machine learning models generalize under such distributional shifts have been a theoretical challenge. Here, we study generalization in kernel regression when the training and test distributions are different using methods from statistical physics. Using the replica method, we derive an analytical formula for the out-of-distribution generalization error applicable to any kernel and real datasets. We identify an overlap matrix that quantifies the mismatch between distributions for a given kernel as a key determinant of generalization performance under distribution shift. Using our analytical expressions we elucidate various generalization phenomena including possible improvement in generalization when there is a mismatch. We develop procedures for optimizing training and test distributions for a given data budget to find best and worst case generalizations under the shift. We present applications of our theory to real and synthetic datasets and for many kernels. We compare results of our theory applied to Neural Tangent Kernel with simulations of wide networks and show agreement. We analyze linear regression in further depth.

Statistical Mechanics of Generalization in Kernel Regression

Generalization beyond a training dataset is a main goal of machine learning. We investigate generalization error in kernel regression using statistical mechanics and derive an analytical expression for it applicable to any kernel. Focusing on the broad class of rotation invariant kernels, which is relevant to training deep neural networks in the infinite-width limit, we show several phenomena. When data is drawn from a spherically symmetric distribution and the number of input dimensions, $D$, is large, we find that multiple learning stages exist, one for each scaling of the number of training samples with $\mathcal{O}_D(D^K)$ with $K\in Z^+$. In each stage $\mathcal{O}_D(D^K)$ degenerate spectral modes corresponding to the $K$-th kernel eigenvalue are learned. The mathematical analysis of a learning stage reduces to that of a solvable model with the dimensionality of the feature space extensive in the number of samples and a white kernel spectrum, including linear regression as a special case. The behavior of the learning curve in each stage is governed by an effective regularizer and an effective target noise that are related to the tail of the kernel and the target function spectra. When effective regularization is zero, we identify a first order phase transition that corresponds to a divergence in the generalization error. Each learning stage can exhibit sample-wise \textit{double-descent}, where learning curves show non-monotonic sample size dependence. For each stage an optimal value of effective regularizer exists, equal to the effective noise variance, that gives minimum generalization error.

Spectrum Dependent Learning Curves in Kernel Regression and Wide Neural Networks

A fundamental question in modern machine learning is how deep neural networks can generalize. We address this question using 1) an equivalence between training infinitely wide neural networks and performing kernel regression with a deterministic kernel called the Neural Tangent Kernel (NTK) (Jacot et al. 2018), and 2) theoretical tools from statistical physics. We derive analytical expressions for learning curves for kernel regression, and use them to evaluate how the test loss of a trained neural network depends on the number of samples. Our approach allows us not only to compute the total test risk but also the decomposition of the risk due to different spectral components of the kernel. Complementary to recent results showing that during gradient descent, neural networks fit low frequency components first, we identify a new type of frequency principle: as the size of the training set size grows, kernel machines and neural networks begin to fit successively higher frequency modes of the target function. We verify our theory with simulations of kernel regression and training wide artificial neural networks.