Bandwidth Enables Generalization in Quantum Kernel Models
Paper and Code
Jun 15, 2022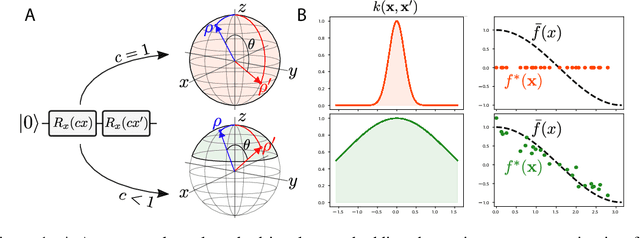

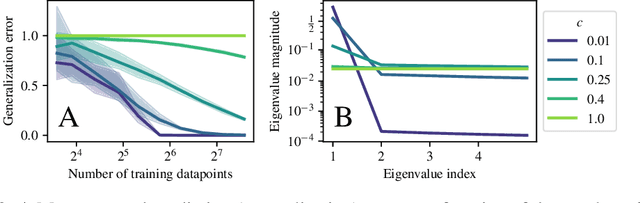
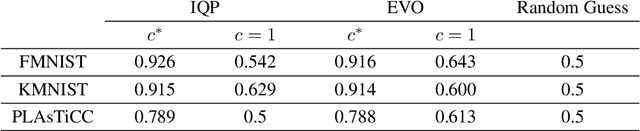
Quantum computers are known to provide speedups over classical state-of-the-art machine learning methods in some specialized settings. For example, quantum kernel methods have been shown to provide an exponential speedup on a learning version of the discrete logarithm problem. Understanding the generalization of quantum models is essential to realizing similar speedups on problems of practical interest. Recent results demonstrate that generalization is hindered by the exponential size of the quantum feature space. Although these results suggest that quantum models cannot generalize when the number of qubits is large, in this paper we show that these results rely on overly restrictive assumptions. We consider a wider class of models by varying a hyperparameter that we call quantum kernel bandwidth. We analyze the large-qubit limit and provide explicit formulas for the generalization of a quantum model that can be solved in closed form. Specifically, we show that changing the value of the bandwidth can take a model from provably not being able to generalize to any target function to good generalization for well-aligned targets. Our analysis shows how the bandwidth controls the spectrum of the kernel integral operator and thereby the inductive bias of the model. We demonstrate empirically that our theory correctly predicts how varying the bandwidth affects generalization of quantum models on challenging datasets, including those far outside our theoretical assumptions. We discuss the implications of our results for quantum advantage in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge