Emergent Manifold Separability during Reasoning in Large Language Models

Chain-of-Thought (CoT) prompting significantly improves reasoning in Large Language Models, yet the temporal dynamics of the underlying representation geometry remain poorly understood. We investigate these dynamics by applying Manifold Capacity Theory (MCT) to a compositional Boolean logic task, allowing us to quantify the linear separability of latent representations without the confounding factors of probe training. Our analysis reveals that reasoning manifests as a transient geometric pulse, where concept manifolds are untangled into linearly separable subspaces immediately prior to computation and rapidly compressed thereafter. This behavior diverges from standard linear probe accuracy, which remains high long after computation, suggesting a fundamental distinction between information that is merely retrievable and information that is geometrically prepared for processing. We interpret this phenomenon as \emph{Dynamic Manifold Management}, a mechanism where the model dynamically modulates representational capacity to optimize the bandwidth of the residual stream throughout the reasoning chain.

Estimating Dimensionality of Neural Representations from Finite Samples

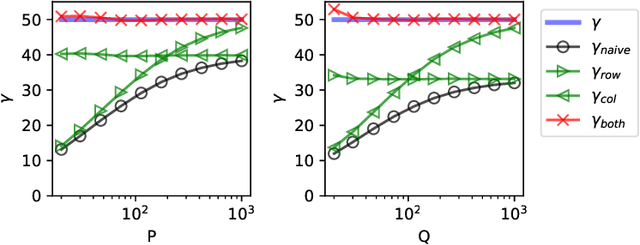
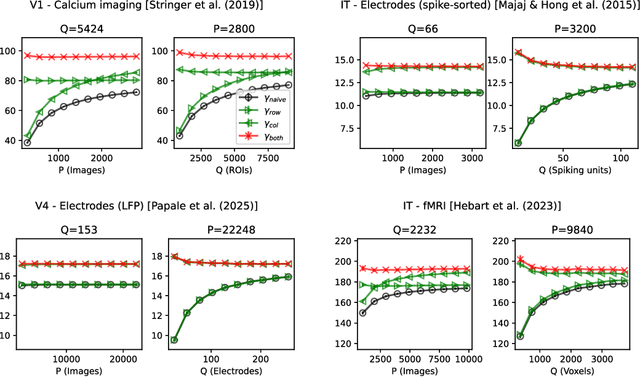
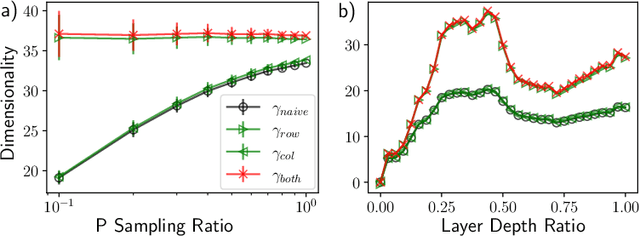
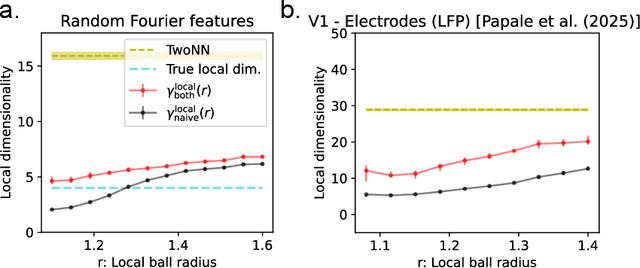
The global dimensionality of a neural representation manifold provides rich insight into the computational process underlying both artificial and biological neural networks. However, all existing measures of global dimensionality are sensitive to the number of samples, i.e., the number of rows and columns of the sample matrix. We show that, in particular, the participation ratio of eigenvalues, a popular measure of global dimensionality, is highly biased with small sample sizes, and propose a bias-corrected estimator that is more accurate with finite samples and with noise. On synthetic data examples, we demonstrate that our estimator can recover the true known dimensionality. We apply our estimator to neural brain recordings, including calcium imaging, electrophysiological recordings, and fMRI data, and to the neural activations in a large language model and show our estimator is invariant to the sample size. Finally, our estimators can additionally be used to measure the local dimensionalities of curved neural manifolds by weighting the finite samples appropriately.

Estimating Neural Representation Alignment from Limited Inputs and Features

In both artificial and biological systems, the centered kernel alignment (CKA) has become a widely used tool for quantifying neural representation similarity. While current CKA estimators typically correct for the effects of finite stimuli sampling, the effects of sampling a subset of neurons are overlooked, introducing notable bias in standard experimental scenarios. Here, we provide a theoretical analysis showing how this bias is affected by the representation geometry. We then introduce a novel estimator that corrects for both input and feature sampling. We use our method for evaluating both brain-to-brain and model-to-brain alignments and show that it delivers reliable comparisons even with very sparsely sampled neurons. We perform within-animal and across-animal comparisons on electrophysiological data from visual cortical areas V1, V4, and IT data, and use these as benchmarks to evaluate model-to-brain alignment. We also apply our method to reveal how object representations become progressively disentangled across layers in both biological and artificial systems. These findings underscore the importance of correcting feature-sampling biases in CKA and demonstrate that our bias-corrected estimator provides a more faithful measure of representation alignment. The improved estimates increase our understanding of how neural activity is structured across both biological and artificial systems.

Estimating the Spectral Moments of the Kernel Integral Operator from Finite Sample Matrices

Analyzing the structure of sampled features from an input data distribution is challenging when constrained by limited measurements in both the number of inputs and features. Traditional approaches often rely on the eigenvalue spectrum of the sample covariance matrix derived from finite measurement matrices; however, these spectra are sensitive to the size of the measurement matrix, leading to biased insights. In this paper, we introduce a novel algorithm that provides unbiased estimates of the spectral moments of the kernel integral operator in the limit of infinite inputs and features from finitely sampled measurement matrices. Our method, based on dynamic programming, is efficient and capable of estimating the moments of the operator spectrum. We demonstrate the accuracy of our estimator on radial basis function (RBF) kernels, highlighting its consistency with the theoretical spectra. Furthermore, we showcase the practical utility and robustness of our method in understanding the geometry of learned representations in neural networks.

Sparsity-depth Tradeoff in Infinitely Wide Deep Neural Networks

We investigate how sparse neural activity affects the generalization performance of a deep Bayesian neural network at the large width limit. To this end, we derive a neural network Gaussian Process (NNGP) kernel with rectified linear unit (ReLU) activation and a predetermined fraction of active neurons. Using the NNGP kernel, we observe that the sparser networks outperform the non-sparse networks at shallow depths on a variety of datasets. We validate this observation by extending the existing theory on the generalization error of kernel-ridge regression.