Sequencing seismograms: A panoptic view of scattering in the core-mantle boundary region

Scattering of seismic waves can reveal subsurface structures but usually in a piecemeal way focused on specific target areas. We used a manifold learning algorithm called "the Sequencer" to simultaneously analyze thousands of seismograms of waves diffracting along the core-mantle boundary and obtain a panoptic view of scattering across the Pacific region. In nearly half of the diffracting waveforms, we detected seismic waves scattered by three-dimensional structures near the core-mantle boundary. The prevalence of these scattered arrivals shows that the region hosts pervasive lateral heterogeneity. Our analysis revealed loud signals due to a plume root beneath Hawaii and a previously unrecognized ultralow-velocity zone beneath the Marquesas Islands. These observations illustrate how approaches flexible enough to detect robust patterns with little to no user supervision can reveal distinctive insights into the deep Earth.

Extracting the main trend in a dataset: the Sequencer algorithm

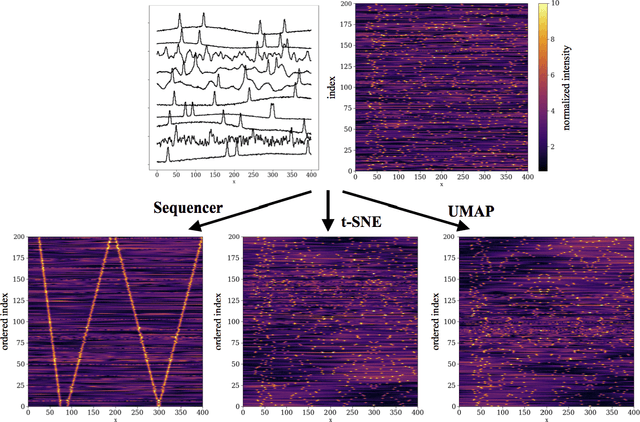
Scientists aim to extract simplicity from observations of the complex world. An important component of this process is the exploration of data in search of trends. In practice, however, this tends to be more of an art than a science. Among all trends existing in the natural world, one-dimensional trends, often called sequences, are of particular interest as they provide insights into simple phenomena. However, some are challenging to detect as they may be expressed in complex manners. We present the Sequencer, an algorithm designed to generically identify the main trend in a dataset. It does so by constructing graphs describing the similarities between pairs of observations, computed with a set of metrics and scales. Using the fact that continuous trends lead to more elongated graphs, the algorithm can identify which aspects of the data are relevant in establishing a global sequence. Such an approach can be used beyond the proposed algorithm and can optimize the parameters of any dimensionality reduction technique. We demonstrate the power of the Sequencer using real-world data from astronomy, geology as well as images from the natural world. We show that, in a number of cases, it outperforms the popular t-SNE and UMAP dimensionality reduction techniques. This approach to exploratory data analysis, which does not rely on training nor tuning of any parameter, has the potential to enable discoveries in a wide range of scientific domains. The source code is available on github and we provide an online interface at \url{http://sequencer.org}.

Probabilistic Random Forest: A machine learning algorithm for noisy datasets

Machine learning (ML) algorithms become increasingly important in the analysis of astronomical data. However, since most ML algorithms are not designed to take data uncertainties into account, ML based studies are mostly restricted to data with high signal-to-noise ratio. Astronomical datasets of such high-quality are uncommon. In this work we modify the long-established Random Forest (RF) algorithm to take into account uncertainties in the measurements (i.e., features) as well as in the assigned classes (i.e., labels). To do so, the Probabilistic Random Forest (PRF) algorithm treats the features and labels as probability distribution functions, rather than deterministic quantities. We perform a variety of experiments where we inject different types of noise to a dataset, and compare the accuracy of the PRF to that of RF. The PRF outperforms RF in all cases, with a moderate increase in running time. We find an improvement in classification accuracy of up to 10% in the case of noisy features, and up to 30% in the case of noisy labels. The PRF accuracy decreased by less then 5% for a dataset with as many as 45% misclassified objects, compared to a clean dataset. Apart from improving the prediction accuracy in noisy datasets, the PRF naturally copes with missing values in the data, and outperforms RF when applied to a dataset with different noise characteristics in the training and test sets, suggesting that it can be used for Transfer Learning.