Taming Score-Based Diffusion Priors for Infinite-Dimensional Nonlinear Inverse Problems

This work introduces a sampling method capable of solving Bayesian inverse problems in function space. It does not assume the log-concavity of the likelihood, meaning that it is compatible with nonlinear inverse problems. The method leverages the recently defined infinite-dimensional score-based diffusion models as a learning-based prior, while enabling provable posterior sampling through a Langevin-type MCMC algorithm defined on function spaces. A novel convergence analysis is conducted, inspired by the fixed-point methods established for traditional regularization-by-denoising algorithms and compatible with weighted annealing. The obtained convergence bound explicitly depends on the approximation error of the score; a well-approximated score is essential to obtain a well-approximated posterior. Stylized and PDE-based examples are provided, demonstrating the validity of our convergence analysis. We conclude by presenting a discussion of the method's challenges related to learning the score and computational complexity.

Removing Bias from Maximum Likelihood Estimation with Model Autophagy

We propose autophagy penalized likelihood estimation (PLE), an unbiased alternative to maximum likelihood estimation (MLE) which is more fair and less susceptible to model autophagy disorder (madness). Model autophagy refers to models trained on their own output; PLE ensures the statistics of these outputs coincide with the data statistics. This enables PLE to be statistically unbiased in certain scenarios where MLE is biased. When biased, MLE unfairly penalizes minority classes in unbalanced datasets and exacerbates the recently discovered issue of self-consuming generative modeling. Theoretical and empirical results show that 1) PLE is more fair to minority classes and 2) PLE is more stable in a self-consumed setting. Furthermore, we provide a scalable and portable implementation of PLE with a hypernetwork framework, allowing existing deep learning architectures to be easily trained with PLE. Finally, we show PLE can bridge the gap between Bayesian and frequentist paradigms in statistics.

ASPIRE: Iterative Amortized Posterior Inference for Bayesian Inverse Problems

Due to their uncertainty quantification, Bayesian solutions to inverse problems are the framework of choice in applications that are risk averse. These benefits come at the cost of computations that are in general, intractable. New advances in machine learning and variational inference (VI) have lowered the computational barrier by learning from examples. Two VI paradigms have emerged that represent different tradeoffs: amortized and non-amortized. Amortized VI can produce fast results but due to generalizing to many observed datasets it produces suboptimal inference results. Non-amortized VI is slower at inference but finds better posterior approximations since it is specialized towards a single observed dataset. Current amortized VI techniques run into a sub-optimality wall that can not be improved without more expressive neural networks or extra training data. We present a solution that enables iterative improvement of amortized posteriors that uses the same networks architectures and training data. The benefits of our method requires extra computations but these remain frugal since they are based on physics-hybrid methods and summary statistics. Importantly, these computations remain mostly offline thus our method maintains cheap and reusable online evaluation while bridging the approximation gap these two paradigms. We denote our proposed method ASPIRE - Amortized posteriors with Summaries that are Physics-based and Iteratively REfined. We first validate our method on a stylized problem with a known posterior then demonstrate its practical use on a high-dimensional and nonlinear transcranial medical imaging problem with ultrasound. Compared with the baseline and previous methods from the literature our method stands out as an computationally efficient and high-fidelity method for posterior inference.

InvertibleNetworks.jl: A Julia package for scalable normalizing flows

InvertibleNetworks.jl is a Julia package designed for the scalable implementation of normalizing flows, a method for density estimation and sampling in high-dimensional distributions. This package excels in memory efficiency by leveraging the inherent invertibility of normalizing flows, which significantly reduces memory requirements during backpropagation compared to existing normalizing flow packages that rely on automatic differentiation frameworks. InvertibleNetworks.jl has been adapted for diverse applications, including seismic imaging, medical imaging, and CO2 monitoring, demonstrating its effectiveness in learning high-dimensional distributions.

Self-Consuming Generative Models Go MAD

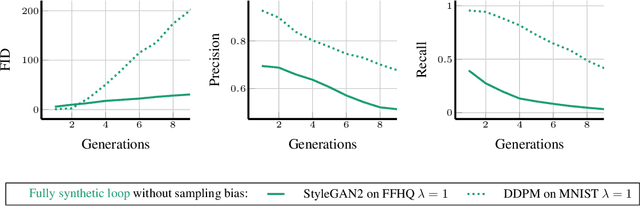
Seismic advances in generative AI algorithms for imagery, text, and other data types has led to the temptation to use synthetic data to train next-generation models. Repeating this process creates an autophagous (self-consuming) loop whose properties are poorly understood. We conduct a thorough analytical and empirical analysis using state-of-the-art generative image models of three families of autophagous loops that differ in how fixed or fresh real training data is available through the generations of training and in whether the samples from previous generation models have been biased to trade off data quality versus diversity. Our primary conclusion across all scenarios is that without enough fresh real data in each generation of an autophagous loop, future generative models are doomed to have their quality (precision) or diversity (recall) progressively decrease. We term this condition Model Autophagy Disorder (MAD), making analogy to mad cow disease.

Conditional score-based diffusion models for Bayesian inference in infinite dimensions

Since their first introduction, score-based diffusion models (SDMs) have been successfully applied to solve a variety of linear inverse problems in finite-dimensional vector spaces due to their ability to efficiently approximate the posterior distribution. However, using SDMs for inverse problems in infinite-dimensional function spaces has only been addressed recently and by learning the unconditional score. While this approach has some advantages, depending on the specific inverse problem at hand, in order to sample from the conditional distribution it needs to incorporate the information from the observed data with a proximal optimization step, solving an optimization problem numerous times. This may not be feasible in inverse problems with computationally costly forward operators. To address these limitations, in this work we propose a method to learn the posterior distribution in infinite-dimensional Bayesian linear inverse problems using amortized conditional SDMs. In particular, we prove that the conditional denoising estimator is a consistent estimator of the conditional score in infinite dimensions. We show that the extension of SDMs to the conditional setting requires some care because the conditional score typically blows up for small times contrarily to the unconditional score. We also discuss the robustness of the learned distribution against perturbations of the observations. We conclude by presenting numerical examples that validate our approach and provide additional insights.

Martian time-series unraveled: A multi-scale nested approach with factorial variational autoencoders

Unsupervised source separation involves unraveling an unknown set of source signals recorded through a mixing operator, with limited prior knowledge about the sources, and only access to a dataset of signal mixtures. This problem is inherently ill-posed and is further challenged by the variety of time-scales exhibited by sources in time series data. Existing methods typically rely on a preselected window size that limits their capacity to handle multi-scale sources. To address this issue, instead of operating in the time domain, we propose an unsupervised multi-scale clustering and source separation framework by leveraging wavelet scattering covariances that provide a low-dimensional representation of stochastic processes, capable of distinguishing between different non-Gaussian stochastic processes. Nested within this representation space, we develop a factorial Gaussian-mixture variational autoencoder that is trained to (1) probabilistically cluster sources at different time-scales and (2) independently sample scattering covariance representations associated with each cluster. Using samples from each cluster as prior information, we formulate source separation as an optimization problem in the wavelet scattering covariance representation space, resulting in separated sources in the time domain. When applied to seismic data recorded during the NASA InSight mission on Mars, our multi-scale nested approach proves to be a powerful tool for discriminating between sources varying greatly in time-scale, e.g., minute-long transient one-sided pulses (known as ``glitches'') and structured ambient noises resulting from atmospheric activities that typically last for tens of minutes. These results provide an opportunity to conduct further investigations into the isolated sources related to atmospheric-surface interactions, thermal relaxations, and other complex phenomena.

Refining Amortized Posterior Approximations using Gradient-Based Summary Statistics

We present an iterative framework to improve the amortized approximations of posterior distributions in the context of Bayesian inverse problems, which is inspired by loop-unrolled gradient descent methods and is theoretically grounded in maximally informative summary statistics. Amortized variational inference is restricted by the expressive power of the chosen variational distribution and the availability of training data in the form of joint data and parameter samples, which often lead to approximation errors such as the amortization gap. To address this issue, we propose an iterative framework that refines the current amortized posterior approximation at each step. Our approach involves alternating between two steps: (1) constructing a training dataset consisting of pairs of summarized data residuals and parameters, where the summarized data residual is generated using a gradient-based summary statistic, and (2) training a conditional generative model -- a normalizing flow in our examples -- on this dataset to obtain a probabilistic update of the unknown parameter. This procedure leads to iterative refinement of the amortized posterior approximations without the need for extra training data. We validate our method in a controlled setting by applying it to a stylized problem, and observe improved posterior approximations with each iteration. Additionally, we showcase the capability of our method in tackling realistically sized problems by applying it to transcranial ultrasound, a high-dimensional, nonlinear inverse problem governed by wave physics, and observe enhanced posterior quality through better image reconstruction with the posterior mean.

Learned multiphysics inversion with differentiable programming and machine learning

We present the Seismic Laboratory for Imaging and Modeling/Monitoring (SLIM) open-source software framework for computational geophysics and, more generally, inverse problems involving the wave-equation (e.g., seismic and medical ultrasound), regularization with learned priors, and learned neural surrogates for multiphase flow simulations. By integrating multiple layers of abstraction, our software is designed to be both readable and scalable. This allows researchers to easily formulate their problems in an abstract fashion while exploiting the latest developments in high-performance computing. We illustrate and demonstrate our design principles and their benefits by means of building a scalable prototype for permeability inversion from time-lapse crosswell seismic data, which aside from coupling of wave physics and multiphase flow, involves machine learning.

Amortized Normalizing Flows for Transcranial Ultrasound with Uncertainty Quantification

We present a novel approach to transcranial ultrasound computed tomography that utilizes normalizing flows to improve the speed of imaging and provide Bayesian uncertainty quantification. Our method combines physics-informed methods and data-driven methods to accelerate the reconstruction of the final image. We make use of a physics-informed summary statistic to incorporate the known ultrasound physics with the goal of compressing large incoming observations. This compression enables efficient training of the normalizing flow and standardizes the size of the data regardless of imaging configurations. The combinations of these methods results in fast uncertainty-aware image reconstruction that generalizes to a variety of transducer configurations. We evaluate our approach with in silico experiments and demonstrate that it can significantly improve the imaging speed while quantifying uncertainty. We validate the quality of our image reconstructions by comparing against the traditional physics-only method and also verify that our provided uncertainty is calibrated with the error.