Learned multiphysics inversion with differentiable programming and machine learning

We present the Seismic Laboratory for Imaging and Modeling/Monitoring (SLIM) open-source software framework for computational geophysics and, more generally, inverse problems involving the wave-equation (e.g., seismic and medical ultrasound), regularization with learned priors, and learned neural surrogates for multiphase flow simulations. By integrating multiple layers of abstraction, our software is designed to be both readable and scalable. This allows researchers to easily formulate their problems in an abstract fashion while exploiting the latest developments in high-performance computing. We illustrate and demonstrate our design principles and their benefits by means of building a scalable prototype for permeability inversion from time-lapse crosswell seismic data, which aside from coupling of wave physics and multiphase flow, involves machine learning.

Towards Large-Scale Learned Solvers for Parametric PDEs with Model-Parallel Fourier Neural Operators

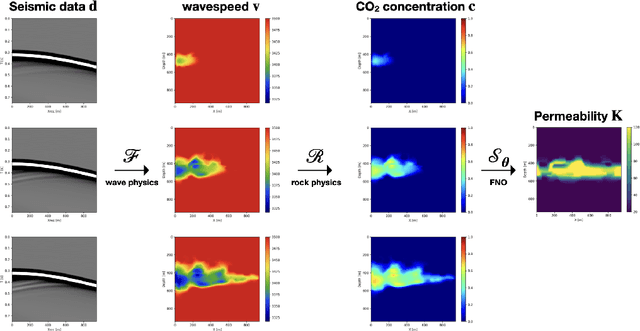
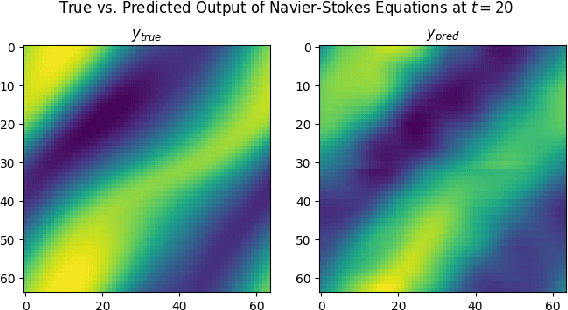
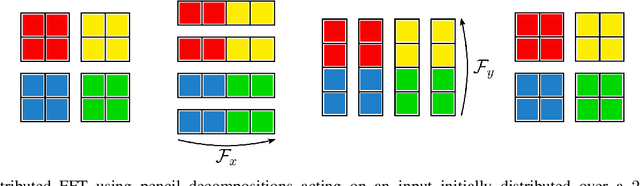
Fourier neural operators (FNOs) are a recently introduced neural network architecture for learning solution operators of partial differential equations (PDEs), which have been shown to perform significantly better than comparable approaches based on convolutional networks. Once trained, FNOs can achieve speed-ups of multiple orders of magnitude over conventional numerical PDE solvers. However, due to the high dimensionality of their input data and network weights, FNOs have so far only been applied to two-dimensional or small three-dimensional problems. To remove this limited problem-size barrier, we propose a model-parallel version of FNOs based on domain-decomposition of both the input data and network weights. We demonstrate that our model-parallel FNO is able to predict time-varying PDE solutions of over 3.2 billions variables on Summit using up to 768 GPUs and show an example of training a distributed FNO on the Azure cloud for simulating multiphase CO$_2$ dynamics in the Earth's subsurface.

A Linear Algebraic Approach to Model Parallelism in Deep Learning

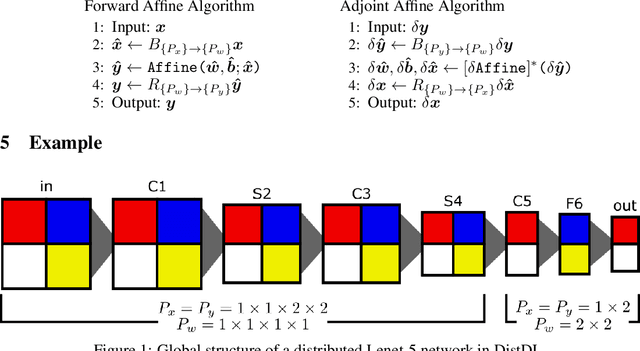
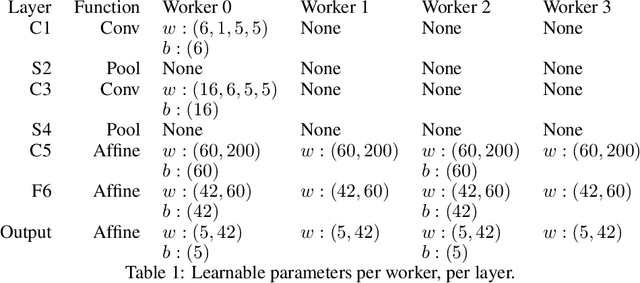
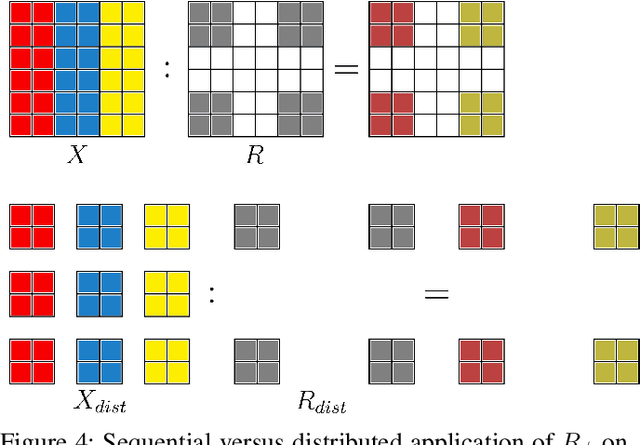
Training deep neural networks (DNNs) in large-cluster computing environments is increasingly necessary, as networks grow in size and complexity. Local memory and processing limitations require robust data and model parallelism for crossing compute node boundaries. We propose a linear-algebraic approach to model parallelism in deep learning, which allows parallel distribution of any tensor in the DNN. Rather than rely on automatic differentiation tools, which do not universally support distributed memory parallelism models, we show that parallel data movement operations, e.g., broadcast, sum-reduce, and halo exchange, are linear operators, and by defining the relevant spaces and inner products, we manually develop the adjoint, or backward, operators required for gradient-based training of DNNs. We build distributed DNN layers using these parallel primitives, composed with sequential layer implementations, and demonstrate their application by building and training a distributed DNN using DistDL, a PyTorch and MPI-based distributed deep learning toolkit.