Removing Bias from Maximum Likelihood Estimation with Model Autophagy

We propose autophagy penalized likelihood estimation (PLE), an unbiased alternative to maximum likelihood estimation (MLE) which is more fair and less susceptible to model autophagy disorder (madness). Model autophagy refers to models trained on their own output; PLE ensures the statistics of these outputs coincide with the data statistics. This enables PLE to be statistically unbiased in certain scenarios where MLE is biased. When biased, MLE unfairly penalizes minority classes in unbalanced datasets and exacerbates the recently discovered issue of self-consuming generative modeling. Theoretical and empirical results show that 1) PLE is more fair to minority classes and 2) PLE is more stable in a self-consumed setting. Furthermore, we provide a scalable and portable implementation of PLE with a hypernetwork framework, allowing existing deep learning architectures to be easily trained with PLE. Finally, we show PLE can bridge the gap between Bayesian and frequentist paradigms in statistics.

Subspace Fitting Meets Regression: The Effects of Supervision and Orthonormality Constraints on Double Descent of Generalization Errors

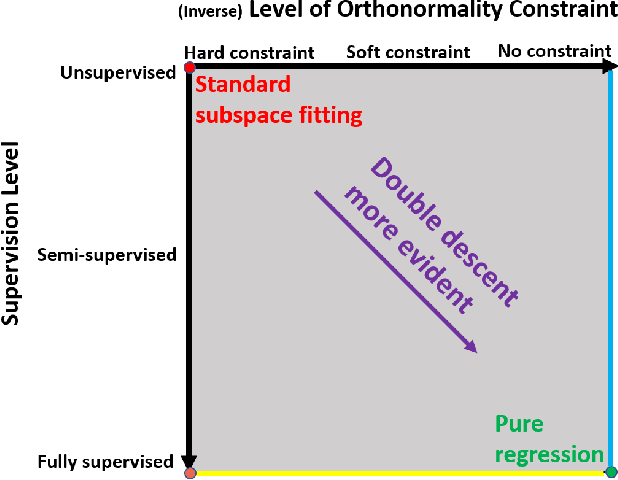
We study the linear subspace fitting problem in the overparameterized setting, where the estimated subspace can perfectly interpolate the training examples. Our scope includes the least-squares solutions to subspace fitting tasks with varying levels of supervision in the training data (i.e., the proportion of input-output examples of the desired low-dimensional mapping) and orthonormality of the vectors defining the learned operator. This flexible family of problems connects standard, unsupervised subspace fitting that enforces strict orthonormality with a corresponding regression task that is fully supervised and does not constrain the linear operator structure. This class of problems is defined over a supervision-orthonormality plane, where each coordinate induces a problem instance with a unique pair of supervision level and softness of orthonormality constraints. We explore this plane and show that the generalization errors of the corresponding subspace fitting problems follow double descent trends as the settings become more supervised and less orthonormally constrained.