Subspace Fitting Meets Regression: The Effects of Supervision and Orthonormality Constraints on Double Descent of Generalization Errors
Paper and Code
Feb 25, 2020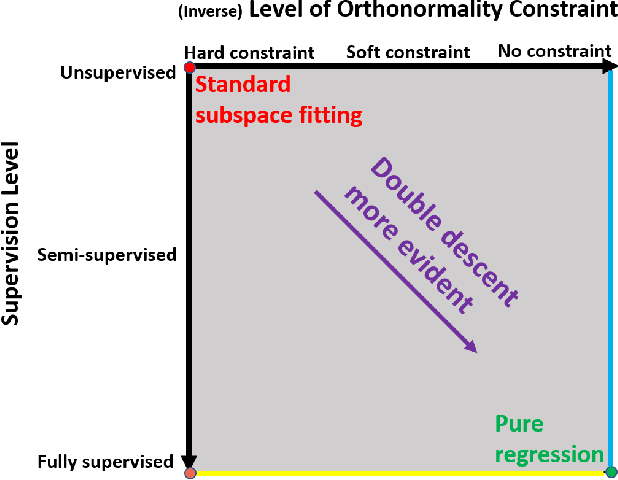



We study the linear subspace fitting problem in the overparameterized setting, where the estimated subspace can perfectly interpolate the training examples. Our scope includes the least-squares solutions to subspace fitting tasks with varying levels of supervision in the training data (i.e., the proportion of input-output examples of the desired low-dimensional mapping) and orthonormality of the vectors defining the learned operator. This flexible family of problems connects standard, unsupervised subspace fitting that enforces strict orthonormality with a corresponding regression task that is fully supervised and does not constrain the linear operator structure. This class of problems is defined over a supervision-orthonormality plane, where each coordinate induces a problem instance with a unique pair of supervision level and softness of orthonormality constraints. We explore this plane and show that the generalization errors of the corresponding subspace fitting problems follow double descent trends as the settings become more supervised and less orthonormally constrained.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge