Self-Improving Diffusion Models with Synthetic Data

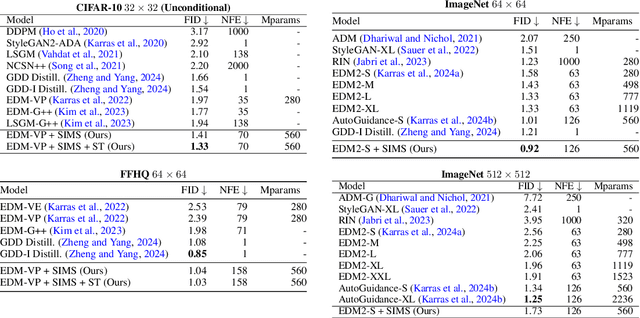
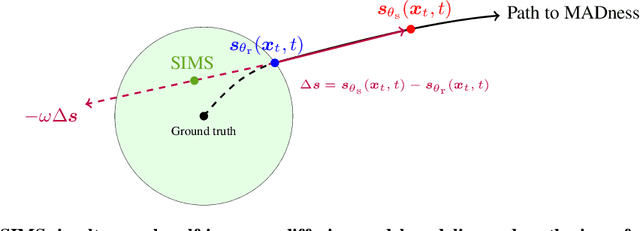
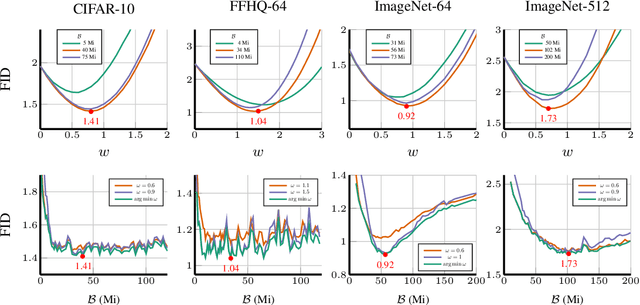
The artificial intelligence (AI) world is running out of real data for training increasingly large generative models, resulting in accelerating pressure to train on synthetic data. Unfortunately, training new generative models with synthetic data from current or past generation models creates an autophagous (self-consuming) loop that degrades the quality and/or diversity of the synthetic data in what has been termed model autophagy disorder (MAD) and model collapse. Current thinking around model autophagy recommends that synthetic data is to be avoided for model training lest the system deteriorate into MADness. In this paper, we take a different tack that treats synthetic data differently from real data. Self-IMproving diffusion models with Synthetic data (SIMS) is a new training concept for diffusion models that uses self-synthesized data to provide negative guidance during the generation process to steer a model's generative process away from the non-ideal synthetic data manifold and towards the real data distribution. We demonstrate that SIMS is capable of self-improvement; it establishes new records based on the Fr\'echet inception distance (FID) metric for CIFAR-10 and ImageNet-64 generation and achieves competitive results on FFHQ-64 and ImageNet-512. Moreover, SIMS is, to the best of our knowledge, the first prophylactic generative AI algorithm that can be iteratively trained on self-generated synthetic data without going MAD. As a bonus, SIMS can adjust a diffusion model's synthetic data distribution to match any desired in-domain target distribution to help mitigate biases and ensure fairness.

An Adaptive Tangent Feature Perspective of Neural Networks

In order to better understand feature learning in neural networks, we propose a framework for understanding linear models in tangent feature space where the features are allowed to be transformed during training. We consider linear transformations of features, resulting in a joint optimization over parameters and transformations with a bilinear interpolation constraint. We show that this optimization problem has an equivalent linearly constrained optimization with structured regularization that encourages approximately low rank solutions. Specializing to neural network structure, we gain insights into how the features and thus the kernel function change, providing additional nuance to the phenomenon of kernel alignment when the target function is poorly represented using tangent features. In addition to verifying our theoretical observations in real neural networks on a simple regression problem, we empirically show that an adaptive feature implementation of tangent feature classification has an order of magnitude lower sample complexity than the fixed tangent feature model on MNIST and CIFAR-10.

Self-Consuming Generative Models Go MAD

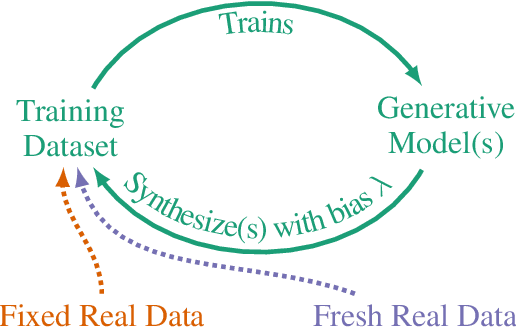
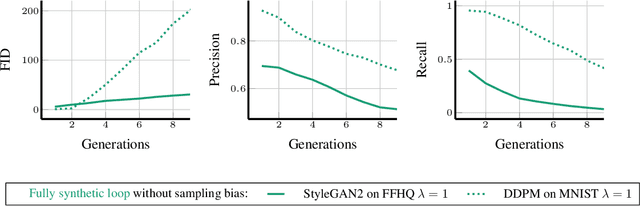
Seismic advances in generative AI algorithms for imagery, text, and other data types has led to the temptation to use synthetic data to train next-generation models. Repeating this process creates an autophagous (self-consuming) loop whose properties are poorly understood. We conduct a thorough analytical and empirical analysis using state-of-the-art generative image models of three families of autophagous loops that differ in how fixed or fresh real training data is available through the generations of training and in whether the samples from previous generation models have been biased to trade off data quality versus diversity. Our primary conclusion across all scenarios is that without enough fresh real data in each generation of an autophagous loop, future generative models are doomed to have their quality (precision) or diversity (recall) progressively decrease. We term this condition Model Autophagy Disorder (MAD), making analogy to mad cow disease.

TITAN: Bringing The Deep Image Prior to Implicit Representations

We study the interpolation capabilities of implicit neural representations (INRs) of images. In principle, INRs promise a number of advantages, such as continuous derivatives and arbitrary sampling, being freed from the restrictions of a raster grid. However, empirically, INRs have been observed to poorly interpolate between the pixels of the fit image; in other words, they do not inherently possess a suitable prior for natural images. In this paper, we propose to address and improve INRs' interpolation capabilities by explicitly integrating image prior information into the INR architecture via deep decoder, a specific implementation of the deep image prior (DIP). Our method, which we call TITAN, leverages a residual connection from the input which enables integrating the principles of the grid-based DIP into the grid-free INR. Through super-resolution and computed tomography experiments, we demonstrate that our method significantly improves upon classic INRs, thanks to the induced natural image bias. We also find that by constraining the weights to be sparse, image quality and sharpness are enhanced, increasing the Lipschitz constant.

NeuroView-RNN: It's About Time

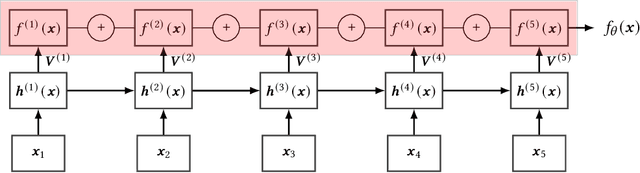
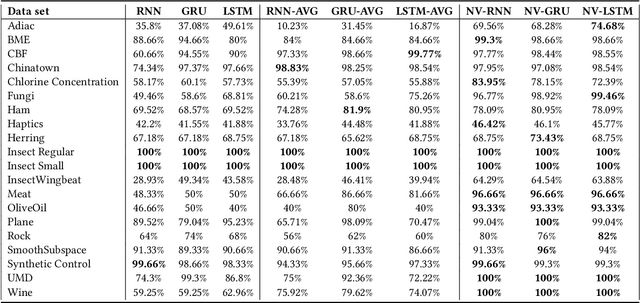
Recurrent Neural Networks (RNNs) are important tools for processing sequential data such as time-series or video. Interpretability is defined as the ability to be understood by a person and is different from explainability, which is the ability to be explained in a mathematical formulation. A key interpretability issue with RNNs is that it is not clear how each hidden state per time step contributes to the decision-making process in a quantitative manner. We propose NeuroView-RNN as a family of new RNN architectures that explains how all the time steps are used for the decision-making process. Each member of the family is derived from a standard RNN architecture by concatenation of the hidden steps into a global linear classifier. The global linear classifier has all the hidden states as the input, so the weights of the classifier have a linear mapping to the hidden states. Hence, from the weights, NeuroView-RNN can quantify how important each time step is to a particular decision. As a bonus, NeuroView-RNN also offers higher accuracy in many cases compared to the RNNs and their variants. We showcase the benefits of NeuroView-RNN by evaluating on a multitude of diverse time-series datasets.

NFT-K: Non-Fungible Tangent Kernels

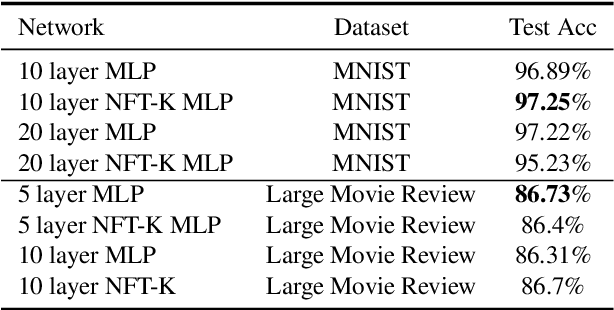
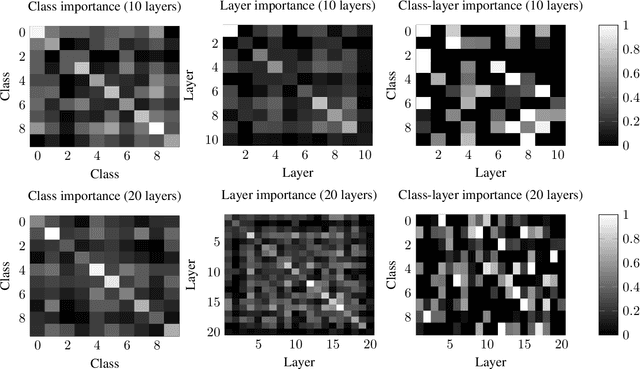
Deep neural networks have become essential for numerous applications due to their strong empirical performance such as vision, RL, and classification. Unfortunately, these networks are quite difficult to interpret, and this limits their applicability in settings where interpretability is important for safety, such as medical imaging. One type of deep neural network is neural tangent kernel that is similar to a kernel machine that provides some aspect of interpretability. To further contribute interpretability with respect to classification and the layers, we develop a new network as a combination of multiple neural tangent kernels, one to model each layer of the deep neural network individually as opposed to past work which attempts to represent the entire network via a single neural tangent kernel. We demonstrate the interpretability of this model on two datasets, showing that the multiple kernels model elucidates the interplay between the layers and predictions.

Scalable Neural Tangent Kernel of Recurrent Architectures

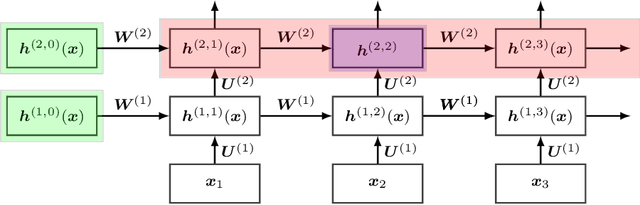
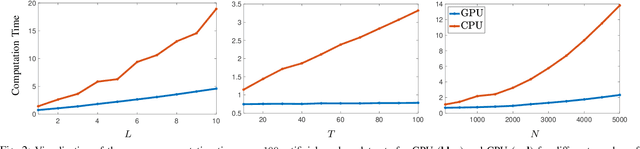
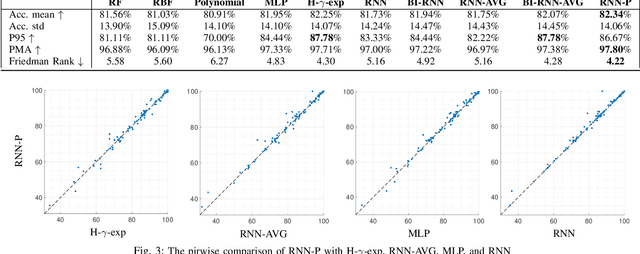
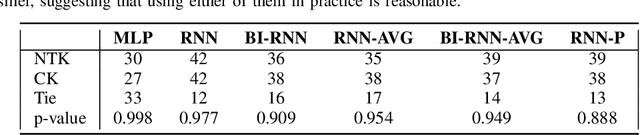
Kernels derived from deep neural networks (DNNs) in the infinite-width provide not only high performance in a range of machine learning tasks but also new theoretical insights into DNN training dynamics and generalization. In this paper, we extend the family of kernels associated with recurrent neural networks (RNNs), which were previously derived only for simple RNNs, to more complex architectures that are bidirectional RNNs and RNNs with average pooling. We also develop a fast GPU implementation to exploit its full practical potential. While RNNs are typically only applied to time-series data, we demonstrate that classifiers using RNN-based kernels outperform a range of baseline methods on 90 non-time-series datasets from the UCI data repository.

Wearing a MASK: Compressed Representations of Variable-Length Sequences Using Recurrent Neural Tangent Kernels

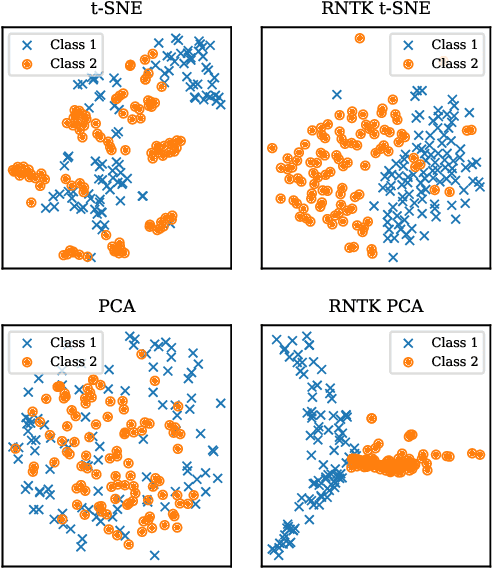
High dimensionality poses many challenges to the use of data, from visualization and interpretation, to prediction and storage for historical preservation. Techniques abound to reduce the dimensionality of fixed-length sequences, yet these methods rarely generalize to variable-length sequences. To address this gap, we extend existing methods that rely on the use of kernels to variable-length sequences via use of the Recurrent Neural Tangent Kernel (RNTK). Since a deep neural network with ReLu activation is a Max-Affine Spline Operator (MASO), we dub our approach Max-Affine Spline Kernel (MASK). We demonstrate how MASK can be used to extend principal components analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) and apply these new algorithms to separate synthetic time series data sampled from second-order differential equations.

The Recurrent Neural Tangent Kernel

The study of deep networks (DNs) in the infinite-width limit, via the so-called Neural Tangent Kernel (NTK) approach, has provided new insights into the dynamics of learning, generalization, and the impact of initialization. One key DN architecture remains to be kernelized, namely, the Recurrent Neural Network (RNN). In this paper we introduce and study the Recurrent Neural Tangent Kernel (RNTK), which sheds new insights into the behavior of overparametrized RNNs, including how different time steps are weighted by the RNTK to form the output under different initialization parameters and nonlinearity choices, and how inputs of different lengths are treated. We demonstrate via a number of experiments that the RNTK offers significant performance gains over other kernels, including standard NTKs across a range of different data sets. A unique benefit of the RNTK is that it is agnostic to the length of the input, in stark contrast to other kernels.