Orb: A Fast, Scalable Neural Network Potential

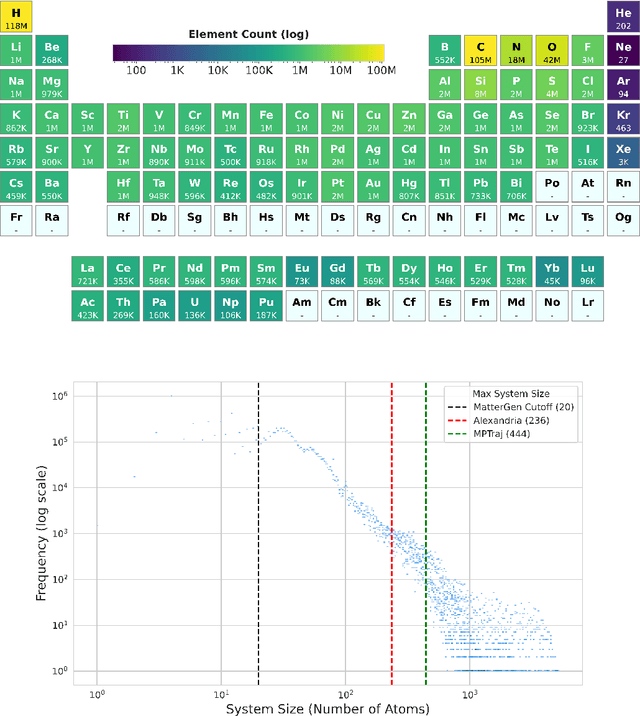
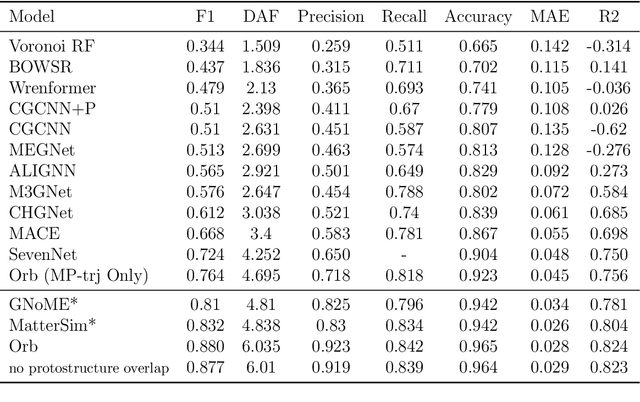
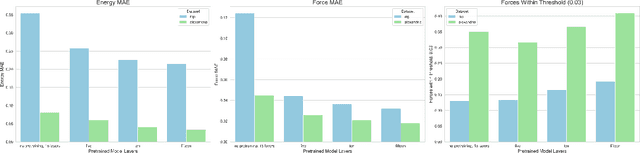
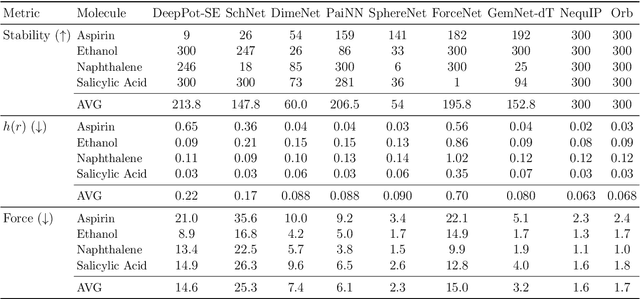
We introduce Orb, a family of universal interatomic potentials for atomistic modelling of materials. Orb models are 3-6 times faster than existing universal potentials, stable under simulation for a range of out of distribution materials and, upon release, represented a 31% reduction in error over other methods on the Matbench Discovery benchmark. We explore several aspects of foundation model development for materials, with a focus on diffusion pretraining. We evaluate Orb as a model for geometry optimization, Monte Carlo and molecular dynamics simulations.

Estimating the Density Ratio between Distributions with High Discrepancy using Multinomial Logistic Regression

Functions of the ratio of the densities $p/q$ are widely used in machine learning to quantify the discrepancy between the two distributions $p$ and $q$. For high-dimensional distributions, binary classification-based density ratio estimators have shown great promise. However, when densities are well separated, estimating the density ratio with a binary classifier is challenging. In this work, we show that the state-of-the-art density ratio estimators perform poorly on well-separated cases and demonstrate that this is due to distribution shifts between training and evaluation time. We present an alternative method that leverages multi-class classification for density ratio estimation and does not suffer from distribution shift issues. The method uses a set of auxiliary densities $\{m_k\}_{k=1}^K$ and trains a multi-class logistic regression to classify the samples from $p, q$, and $\{m_k\}_{k=1}^K$ into $K+2$ classes. We show that if these auxiliary densities are constructed such that they overlap with $p$ and $q$, then a multi-class logistic regression allows for estimating $\log p/q$ on the domain of any of the $K+2$ distributions and resolves the distribution shift problems of the current state-of-the-art methods. We compare our method to state-of-the-art density ratio estimators on both synthetic and real datasets and demonstrate its superior performance on the tasks of density ratio estimation, mutual information estimation, and representation learning. Code: https://www.blackswhan.com/mdre/

Enhanced gradient-based MCMC in discrete spaces

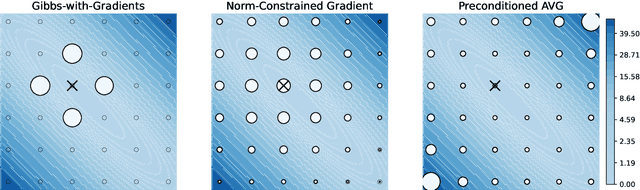
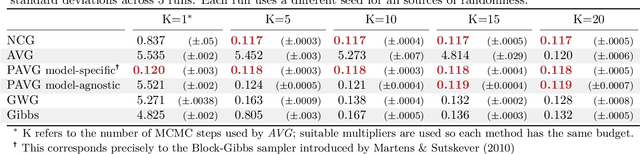
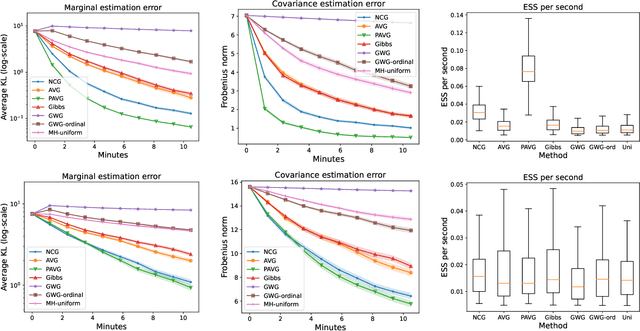
The recent introduction of gradient-based MCMC for discrete spaces holds great promise, and comes with the tantalising possibility of new discrete counterparts to celebrated continuous methods such as MALA and HMC. Towards this goal, we introduce several discrete Metropolis-Hastings samplers that are conceptually-inspired by MALA, and demonstrate their strong empirical performance across a range of challenging sampling problems in Bayesian inference and energy-based modelling. Methodologically, we identify why discrete analogues to preconditioned MALA are generally intractable, motivating us to introduce a new kind of preconditioning based on auxiliary variables and the `Gaussian integral trick'.

Statistical applications of contrastive learning

The likelihood function plays a crucial role in statistical inference and experimental design. However, it is computationally intractable for several important classes of statistical models, including energy-based models and simulator-based models. Contrastive learning is an intuitive and computationally feasible alternative to likelihood-based learning. We here first provide an introduction to contrastive learning and then show how we can use it to derive methods for diverse statistical problems, namely parameter estimation for energy-based models, Bayesian inference for simulator-based models, as well as experimental design.

Variational Gibbs inference for statistical model estimation from incomplete data

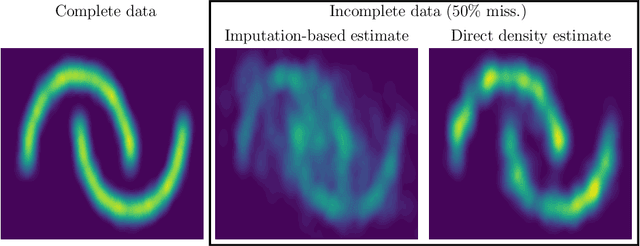
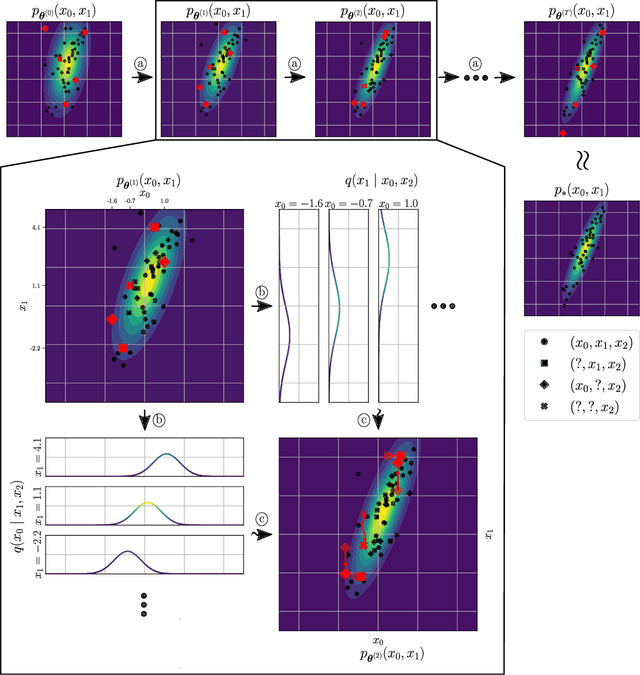
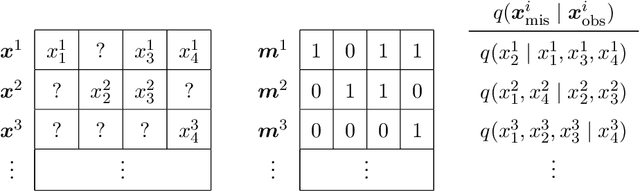
Statistical models are central to machine learning with broad applicability across a range of downstream tasks. The models are typically controlled by free parameters that are estimated from data by maximum-likelihood estimation. However, when faced with real-world datasets many of the models run into a critical issue: they are formulated in terms of fully-observed data, whereas in practice the datasets are plagued with missing data. The theory of statistical model estimation from incomplete data is conceptually similar to the estimation of latent-variable models, where powerful tools such as variational inference (VI) exist. However, in contrast to standard latent-variable models, parameter estimation with incomplete data often requires estimating exponentially-many conditional distributions of the missing variables, hence making standard VI methods intractable. We address this gap by introducing variational Gibbs inference (VGI), a new general-purpose method to estimate the parameters of statistical models from incomplete data. We validate VGI on a set of synthetic and real-world estimation tasks, estimating important machine learning models, VAEs and normalising flows, from incomplete data. The proposed method, whilst general-purpose, achieves competitive or better performance than existing model-specific estimation methods.

Telescoping Density-Ratio Estimation

Density-ratio estimation via classification is a cornerstone of unsupervised learning. It has provided the foundation for state-of-the-art methods in representation learning and generative modelling, with the number of use-cases continuing to proliferate. However, it suffers from a critical limitation: it fails to accurately estimate ratios p/q for which the two densities differ significantly. Empirically, we find this occurs whenever the KL divergence between p and q exceeds tens of nats. To resolve this limitation, we introduce a new framework, telescoping density-ratio estimation (TRE), that enables the estimation of ratios between highly dissimilar densities in high-dimensional spaces. Our experiments demonstrate that TRE can yield substantial improvements over existing single-ratio methods for mutual information estimation, representation learning and energy-based modelling.

Variational Noise-Contrastive Estimation

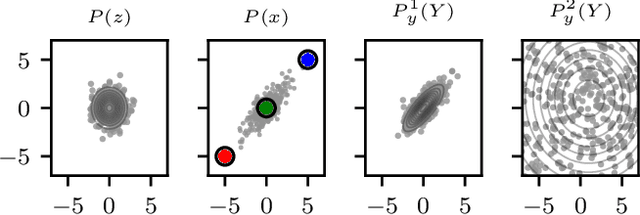
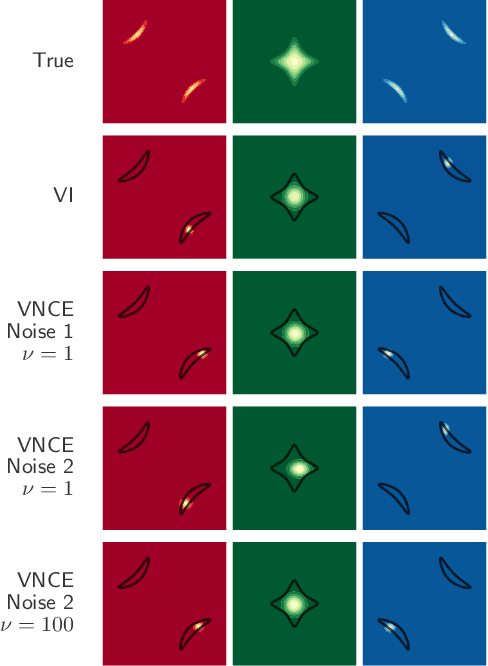
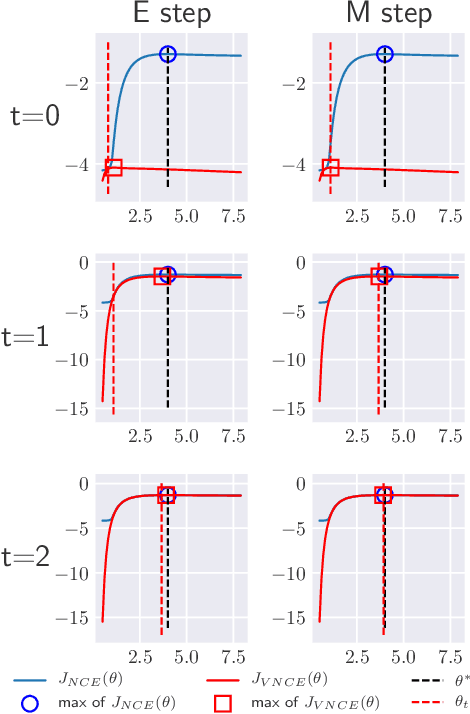
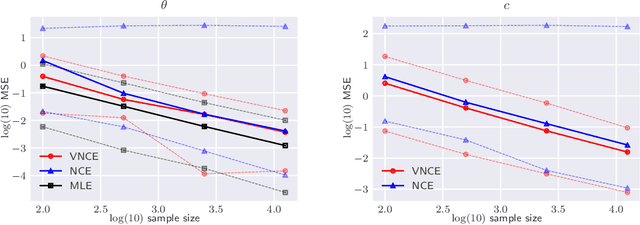
Unnormalised latent variable models are a broad and flexible class of statistical models. However, learning their parameters from data is intractable, and few estimation techniques are currently available for such models. To increase the number of techniques in our arsenal, we propose variational noise-contrastive estimation (VNCE), building on NCE which is a method that only applies to unnormalised models. The core idea is to use a variational lower bound to the NCE objective function, which can be optimised in the same fashion as the evidence lower bound (ELBO) in standard variational inference (VI). We prove that VNCE can be used for both parameter estimation of unnormalised models and posterior inference of latent variables. The developed theory shows that VNCE has the same level of generality as standard VI, meaning that advances made there can be directly imported to the unnormalised setting. We validate VNCE on toy models and apply it to a realistic problem of estimating an undirected graphical model from incomplete data.