Michael Gutmann
Fast and Robust Simulation-Based Inference With Optimization Monte Carlo
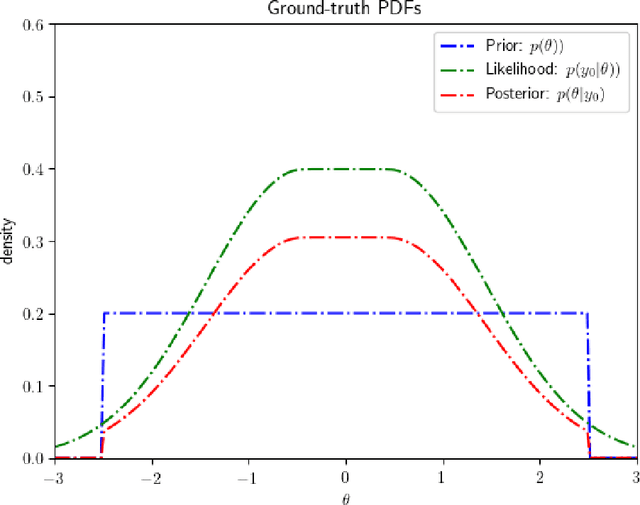
Nov 17, 2025Abstract:Bayesian parameter inference for complex stochastic simulators is challenging due to intractable likelihood functions. Existing simulation-based inference methods often require large number of simulations and become costly to use in high-dimensional parameter spaces or in problems with partially uninformative outputs. We propose a new method for differentiable simulators that delivers accurate posterior inference with substantially reduced runtimes. Building on the Optimization Monte Carlo framework, our approach reformulates stochastic simulation as deterministic optimization problems. Gradient-based methods are then applied to efficiently navigate toward high-density posterior regions and avoid wasteful simulations in low-probability areas. A JAX-based implementation further enhances the performance through vectorization of key method components. Extensive experiments, including high-dimensional parameter spaces, uninformative outputs, multiple observations and multimodal posteriors show that our method consistently matches, and often exceeds, the accuracy of state-of-the-art approaches, while reducing the runtime by a substantial margin.
An Extendable Python Implementation of Robust Optimisation Monte Carlo
Sep 19, 2023



Abstract:Performing inference in statistical models with an intractable likelihood is challenging, therefore, most likelihood-free inference (LFI) methods encounter accuracy and efficiency limitations. In this paper, we present the implementation of the LFI method Robust Optimisation Monte Carlo (ROMC) in the Python package ELFI. ROMC is a novel and efficient (highly-parallelizable) LFI framework that provides accurate weighted samples from the posterior. Our implementation can be used in two ways. First, a scientist may use it as an out-of-the-box LFI algorithm; we provide an easy-to-use API harmonized with the principles of ELFI, enabling effortless comparisons with the rest of the methods included in the package. Additionally, we have carefully split ROMC into isolated components for supporting extensibility. A researcher may experiment with novel method(s) for solving part(s) of ROMC without reimplementing everything from scratch. In both scenarios, the ROMC parts can run in a fully-parallelized manner, exploiting all CPU cores. We also provide helpful functionalities for (i) inspecting the inference process and (ii) evaluating the obtained samples. Finally, we test the robustness of our implementation on some typical LFI examples.
Enhanced gradient-based MCMC in discrete spaces
Jul 29, 2022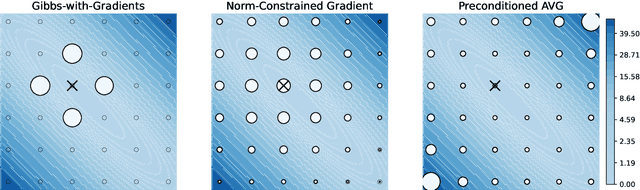
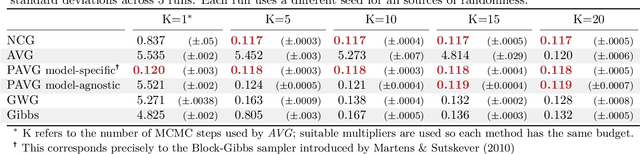
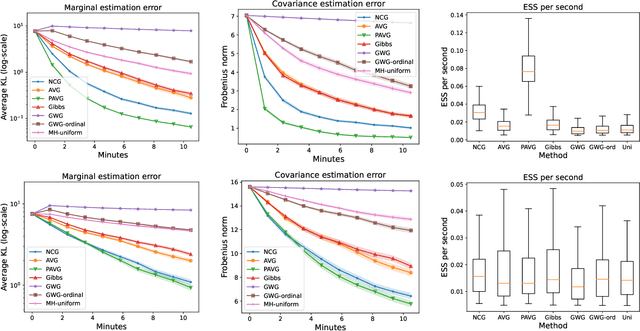

Abstract:The recent introduction of gradient-based MCMC for discrete spaces holds great promise, and comes with the tantalising possibility of new discrete counterparts to celebrated continuous methods such as MALA and HMC. Towards this goal, we introduce several discrete Metropolis-Hastings samplers that are conceptually-inspired by MALA, and demonstrate their strong empirical performance across a range of challenging sampling problems in Bayesian inference and energy-based modelling. Methodologically, we identify why discrete analogues to preconditioned MALA are generally intractable, motivating us to introduce a new kind of preconditioning based on auxiliary variables and the `Gaussian integral trick'.
Extending the statistical software package Engine for Likelihood-Free Inference
Nov 08, 2020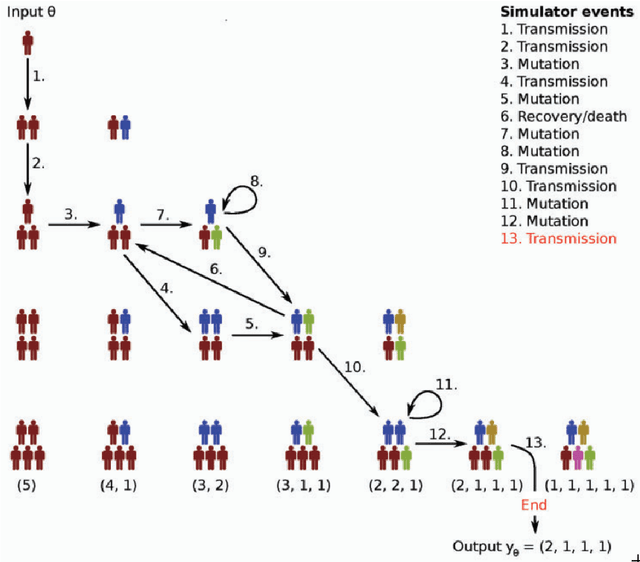


Abstract:Bayesian inference is a principled framework for dealing with uncertainty. The practitioner can perform an initial assumption for the physical phenomenon they want to model (prior belief), collect some data and then adjust the initial assumption in the light of the new evidence (posterior belief). Approximate Bayesian Computation (ABC) methods, also known as likelihood-free inference techniques, are a class of models used for performing inference when the likelihood is intractable. The unique requirement of these models is a black-box sampling machine. Due to the modelling-freedom they provide these approaches are particularly captivating. Robust Optimisation Monte Carlo (ROMC) is one of the most recent techniques of the specific domain. It approximates the posterior distribution by solving independent optimisation problems. This dissertation focuses on the implementation of the ROMC method in the software package Engine for Likelihood-Free Inference (ELFI). In the first chapters, we provide the mathematical formulation and the algorithmic description of the ROMC approach. In the following chapters, we describe our implementation; (a) we present all the functionalities provided to the user and (b) we demonstrate how to perform inference on some real examples. Our implementation provides a robust and efficient solution to a practitioner who wants to perform inference on a simulator-based model. Furthermore, it exploits parallel processing for accelerating the inference wherever it is possible. Finally, it has been designed to serve extensibility; the user can easily replace specific subparts of the method without significant overhead on the development side. Therefore, it can be used by a researcher for further experimentation.
Neural Approximate Sufficient Statistics for Implicit Models
Oct 20, 2020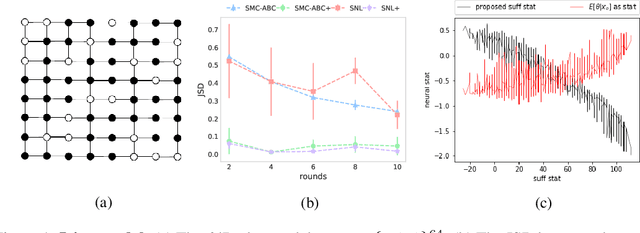

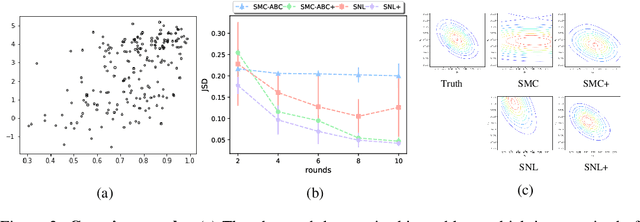

Abstract:We consider the fundamental problem of how to automatically construct summary statistics for implicit generative models where the evaluation of likelihood function is intractable but sampling / simulating data from the model is possible. The idea is to frame the task of constructing sufficient statistics as learning mutual information maximizing representation of the data. This representation is computed by a deep neural network trained by a joint statistic-posterior learning strategy. We apply our approach to both traditional approximate Bayesian computation (ABC) and recent neural likelihood approaches, boosting their performance on a range of tasks.
Parallel Gaussian process surrogate method to accelerate likelihood-free inference
May 03, 2019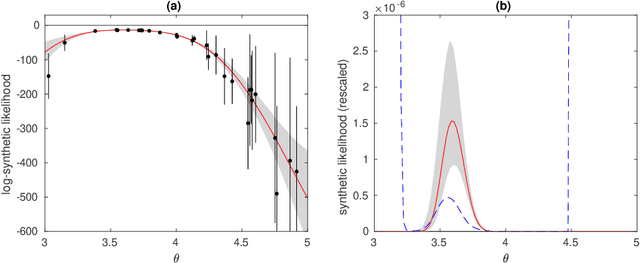

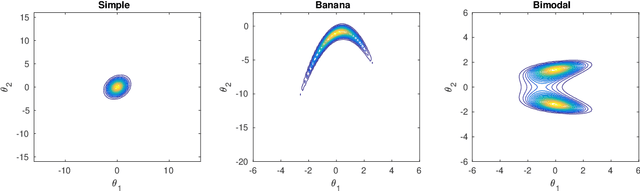
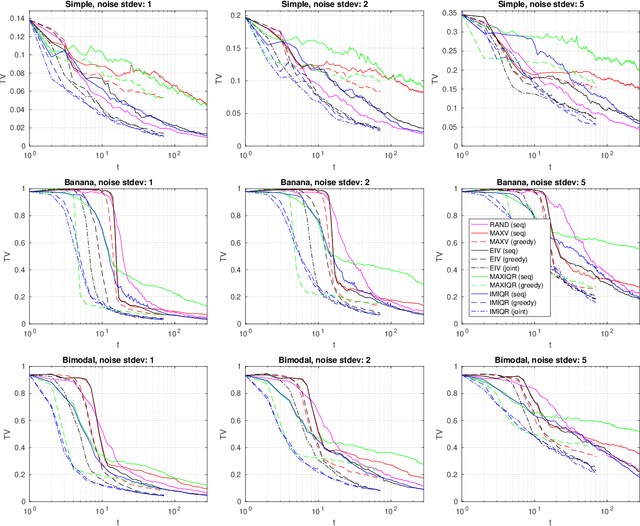
Abstract:We consider Bayesian inference when only a limited number of noisy log-likelihood evaluations can be obtained. This occurs for example when complex simulator-based statistical models are fitted to data, and synthetic likelihood (SL) is used to form the noisy log-likelihood estimates using computationally costly forward simulations. We frame the inference task as a Bayesian sequential design problem, where the log-likelihood function is modelled with a hierarchical Gaussian process (GP) surrogate model, which is used to efficiently select additional log-likelihood evaluation locations. Motivated by recent progress in batch Bayesian optimisation, we develop various batch-sequential strategies where multiple simulations are adaptively selected to minimise either the expected or median loss function measuring the uncertainty in the resulting posterior. We analyse the properties of the resulting method theoretically and empirically. Experiments with toy problems and three simulation models suggest that our method is robust, highly parallelisable, and sample-efficient.
Efficient Bayesian Experimental Design for Implicit Models
Oct 23, 2018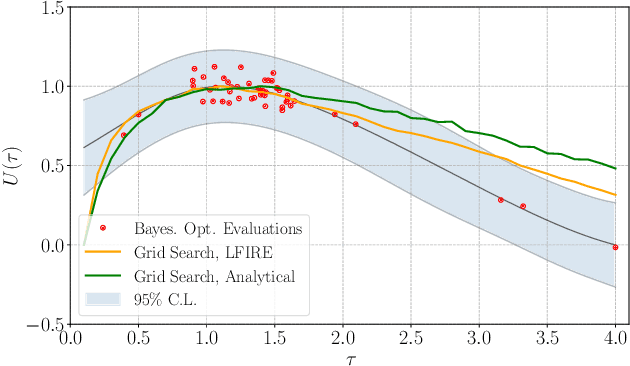
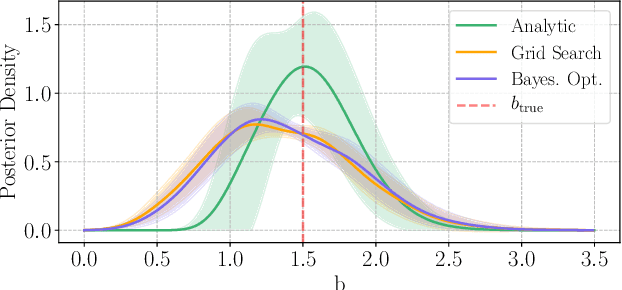
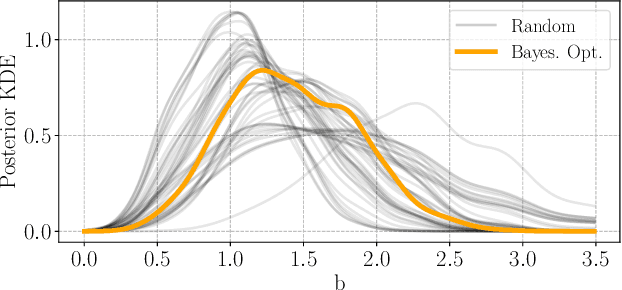
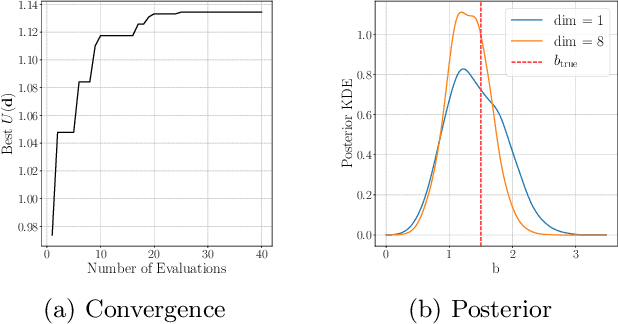
Abstract:Bayesian experimental design involves the optimal allocation of resources in an experiment, with the aim of optimising cost and performance. For implicit models, where the likelihood is intractable but sampling from the model is possible, this task is particularly difficult and therefore largely unexplored. This is mainly due to technical difficulties associated with approximating posterior distributions and utility functions. We devise a novel experimental design framework for implicit models that improves upon previous work in two ways. First, we use the mutual information between parameters and data as the utility function, which has previously not been feasible. We achieve this by utilising Likelihood-Free Inference by Ratio Estimation (LFIRE) to approximate posterior distributions, instead of the traditional approximate Bayesian computation or synthetic likelihood methods. Secondly, we use Bayesian optimisation in order to solve the optimal design problem, as opposed to the typically used grid search. We find that this increases efficiency and allows us to consider higher design dimensions.
Variational Noise-Contrastive Estimation
Oct 19, 2018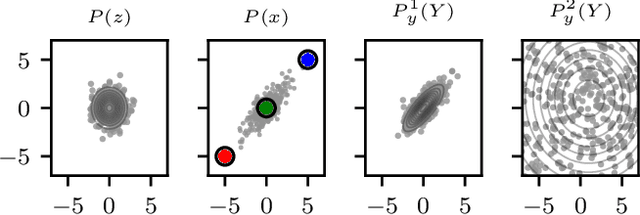
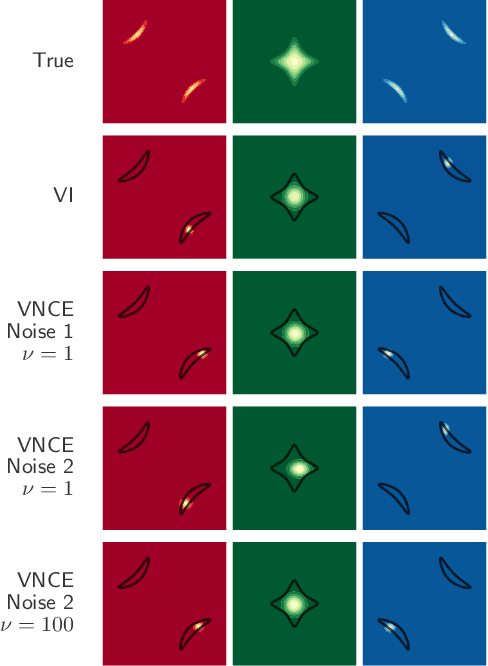
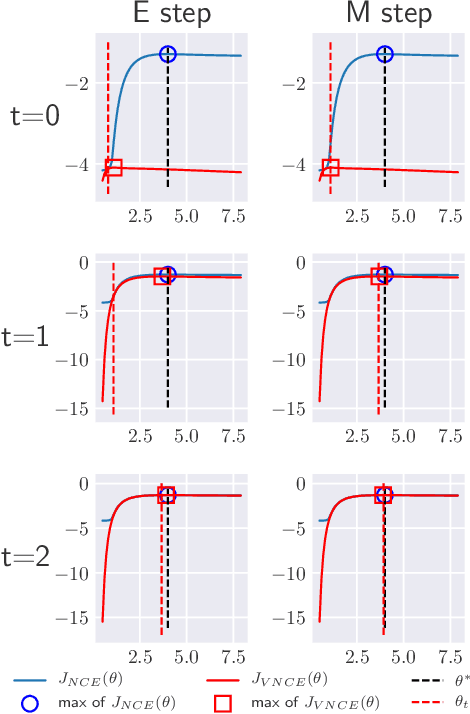
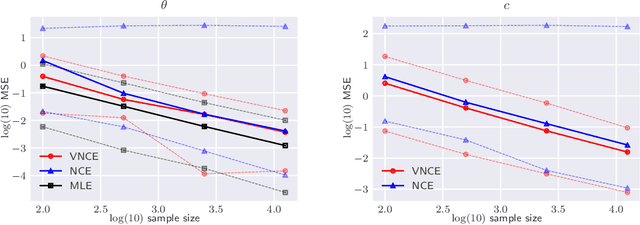
Abstract:Unnormalised latent variable models are a broad and flexible class of statistical models. However, learning their parameters from data is intractable, and few estimation techniques are currently available for such models. To increase the number of techniques in our arsenal, we propose variational noise-contrastive estimation (VNCE), building on NCE which is a method that only applies to unnormalised models. The core idea is to use a variational lower bound to the NCE objective function, which can be optimised in the same fashion as the evidence lower bound (ELBO) in standard variational inference (VI). We prove that VNCE can be used for both parameter estimation of unnormalised models and posterior inference of latent variables. The developed theory shows that VNCE has the same level of generality as standard VI, meaning that advances made there can be directly imported to the unnormalised setting. We validate VNCE on toy models and apply it to a realistic problem of estimating an undirected graphical model from incomplete data.
Gaussian process modeling in approximate Bayesian computation to estimate horizontal gene transfer in bacteria
Feb 16, 2018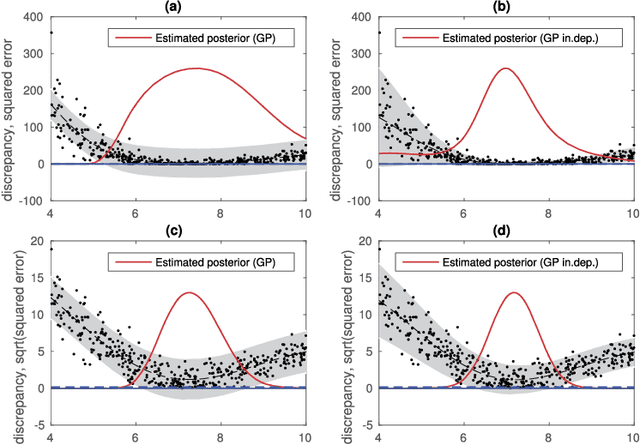

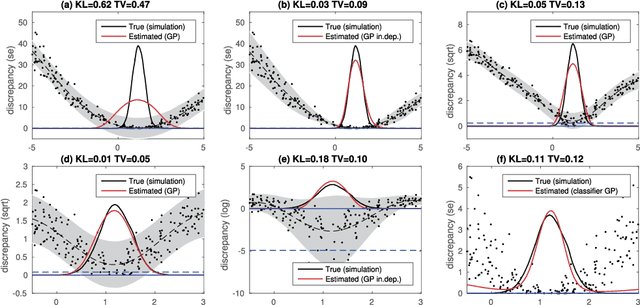
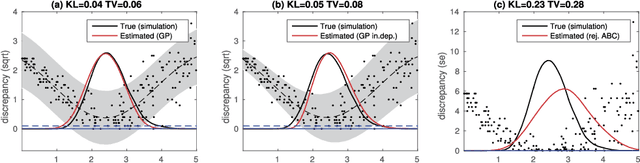
Abstract:Approximate Bayesian computation (ABC) can be used for model fitting when the likelihood function is intractable but simulating from the model is feasible. However, even a single evaluation of a complex model may take several hours, limiting the number of model evaluations available. Modelling the discrepancy between the simulated and observed data using a Gaussian process (GP) can be used to reduce the number of model evaluations required by ABC, but the sensitivity of this approach to a specific GP formulation has not yet been thoroughly investigated. We begin with a comprehensive empirical evaluation of using GPs in ABC, including various transformations of the discrepancies and two novel GP formulations. Our results indicate the choice of GP may significantly affect the accuracy of the estimated posterior distribution. Selection of an appropriate GP model is thus important. We formulate expected utility to measure the accuracy of classifying discrepancies below or above the ABC threshold, and show that it can be used to automate the GP model selection step. Finally, based on the understanding gained with toy examples, we fit a population genetic model for bacteria, providing insight into horizontal gene transfer events within the population and from external origins.
A Family of Computationally Efficient and Simple Estimators for Unnormalized Statistical Models
Mar 15, 2012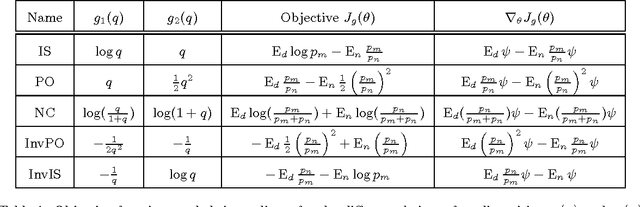
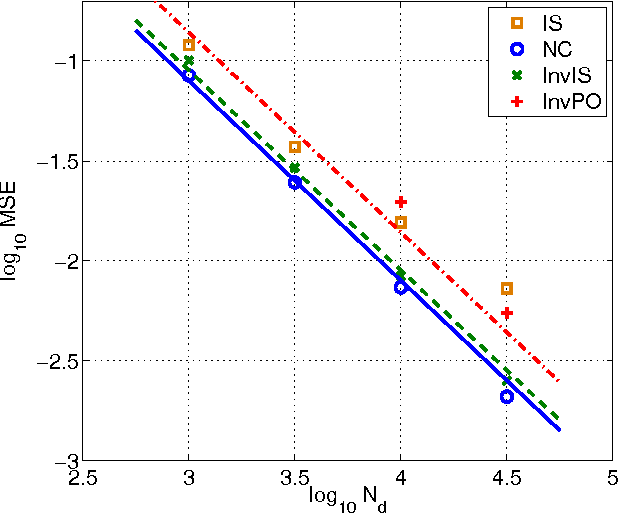


Abstract:We introduce a new family of estimators for unnormalized statistical models. Our family of estimators is parameterized by two nonlinear functions and uses a single sample from an auxiliary distribution, generalizing Maximum Likelihood Monte Carlo estimation of Geyer and Thompson (1992). The family is such that we can estimate the partition function like any other parameter in the model. The estimation is done by optimizing an algebraically simple, well defined objective function, which allows for the use of dedicated optimization methods. We establish consistency of the estimator family and give an expression for the asymptotic covariance matrix, which enables us to further analyze the influence of the nonlinearities and the auxiliary density on estimation performance. Some estimators in our family are particularly stable for a wide range of auxiliary densities. Interestingly, a specific choice of the nonlinearity establishes a connection between density estimation and classification by nonlinear logistic regression. Finally, the optimal amount of auxiliary samples relative to the given amount of the data is considered from the perspective of computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge