Bregman divergence as general framework to estimate unnormalized statistical models
Paper and Code
Feb 14, 2012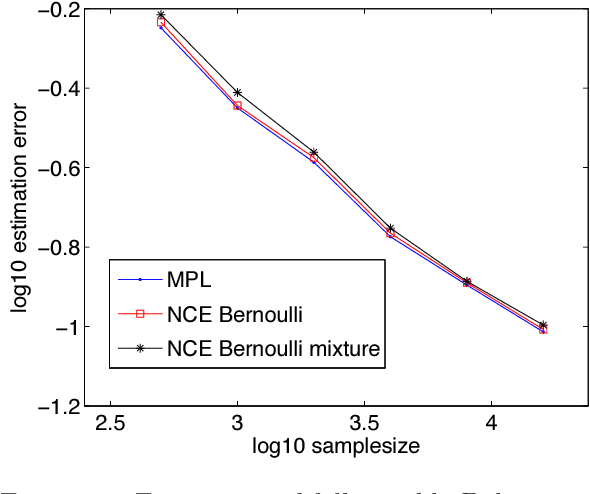
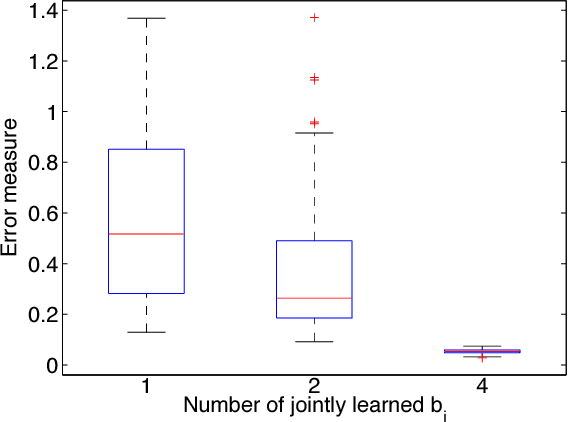
We show that the Bregman divergence provides a rich framework to estimate unnormalized statistical models for continuous or discrete random variables, that is, models which do not integrate or sum to one, respectively. We prove that recent estimation methods such as noise-contrastive estimation, ratio matching, and score matching belong to the proposed framework, and explain their interconnection based on supervised learning. Further, we discuss the role of boosting in unsupervised learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge