Effector: A Python package for regional explanations

Global feature effect methods explain a model outputting one plot per feature. The plot shows the average effect of the feature on the output, like the effect of age on the annual income. However, average effects may be misleading when derived from local effects that are heterogeneous, i.e., they significantly deviate from the average. To decrease the heterogeneity, regional effects provide multiple plots per feature, each representing the average effect within a specific subspace. For interpretability, subspaces are defined as hyperrectangles defined by a chain of logical rules, like age's effect on annual income separately for males and females and different levels of professional experience. We introduce Effector, a Python library dedicated to regional feature effects. Effector implements well-established global effect methods, assesses the heterogeneity of each method and, based on that, provides regional effects. Effector automatically detects subspaces where regional effects have reduced heterogeneity. All global and regional effect methods share a common API, facilitating comparisons between them. Moreover, the library's interface is extensible so new methods can be easily added and benchmarked. The library has been thoroughly tested, ships with many tutorials (https://xai-effector.github.io/) and is available under an open-source license at PyPi (https://pypi.org/project/effector/) and Github (https://github.com/givasile/effector).

Regionally Additive Models: Explainable-by-design models minimizing feature interactions

Generalized Additive Models (GAMs) are widely used explainable-by-design models in various applications. GAMs assume that the output can be represented as a sum of univariate functions, referred to as components. However, this assumption fails in ML problems where the output depends on multiple features simultaneously. In these cases, GAMs fail to capture the interaction terms of the underlying function, leading to subpar accuracy. To (partially) address this issue, we propose Regionally Additive Models (RAMs), a novel class of explainable-by-design models. RAMs identify subregions within the feature space where interactions are minimized. Within these regions, it is more accurate to express the output as a sum of univariate functions (components). Consequently, RAMs fit one component per subregion of each feature instead of one component per feature. This approach yields a more expressive model compared to GAMs while retaining interpretability. The RAM framework consists of three steps. Firstly, we train a black-box model. Secondly, using Regional Effect Plots, we identify subregions where the black-box model exhibits near-local additivity. Lastly, we fit a GAM component for each identified subregion. We validate the effectiveness of RAMs through experiments on both synthetic and real-world datasets. The results confirm that RAMs offer improved expressiveness compared to GAMs while maintaining interpretability.

RHALE: Robust and Heterogeneity-aware Accumulated Local Effects

Accumulated Local Effects (ALE) is a widely-used explainability method for isolating the average effect of a feature on the output, because it handles cases with correlated features well. However, it has two limitations. First, it does not quantify the deviation of instance-level (local) effects from the average (global) effect, known as heterogeneity. Second, for estimating the average effect, it partitions the feature domain into user-defined, fixed-sized bins, where different bin sizes may lead to inconsistent ALE estimations. To address these limitations, we propose Robust and Heterogeneity-aware ALE (RHALE). RHALE quantifies the heterogeneity by considering the standard deviation of the local effects and automatically determines an optimal variable-size bin-splitting. In this paper, we prove that to achieve an unbiased approximation of the standard deviation of local effects within each bin, bin splitting must follow a set of sufficient conditions. Based on these conditions, we propose an algorithm that automatically determines the optimal partitioning, balancing the estimation bias and variance. Through evaluations on synthetic and real datasets, we demonstrate the superiority of RHALE compared to other methods, including the advantages of automatic bin splitting, especially in cases with correlated features.

An Extendable Python Implementation of Robust Optimisation Monte Carlo

Performing inference in statistical models with an intractable likelihood is challenging, therefore, most likelihood-free inference (LFI) methods encounter accuracy and efficiency limitations. In this paper, we present the implementation of the LFI method Robust Optimisation Monte Carlo (ROMC) in the Python package ELFI. ROMC is a novel and efficient (highly-parallelizable) LFI framework that provides accurate weighted samples from the posterior. Our implementation can be used in two ways. First, a scientist may use it as an out-of-the-box LFI algorithm; we provide an easy-to-use API harmonized with the principles of ELFI, enabling effortless comparisons with the rest of the methods included in the package. Additionally, we have carefully split ROMC into isolated components for supporting extensibility. A researcher may experiment with novel method(s) for solving part(s) of ROMC without reimplementing everything from scratch. In both scenarios, the ROMC parts can run in a fully-parallelized manner, exploiting all CPU cores. We also provide helpful functionalities for (i) inspecting the inference process and (ii) evaluating the obtained samples. Finally, we test the robustness of our implementation on some typical LFI examples.

DALE: Differential Accumulated Local Effects for efficient and accurate global explanations

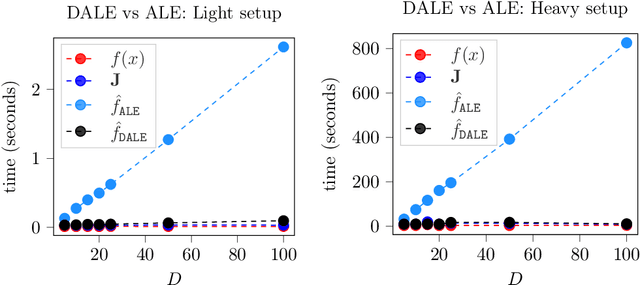
Accumulated Local Effect (ALE) is a method for accurately estimating feature effects, overcoming fundamental failure modes of previously-existed methods, such as Partial Dependence Plots. However, ALE's approximation, i.e. the method for estimating ALE from the limited samples of the training set, faces two weaknesses. First, it does not scale well in cases where the input has high dimensionality, and, second, it is vulnerable to out-of-distribution (OOD) sampling when the training set is relatively small. In this paper, we propose a novel ALE approximation, called Differential Accumulated Local Effects (DALE), which can be used in cases where the ML model is differentiable and an auto-differentiable framework is accessible. Our proposal has significant computational advantages, making feature effect estimation applicable to high-dimensional Machine Learning scenarios with near-zero computational overhead. Furthermore, DALE does not create artificial points for calculating the feature effect, resolving misleading estimations due to OOD sampling. Finally, we formally prove that, under some hypotheses, DALE is an unbiased estimator of ALE and we present a method for quantifying the standard error of the explanation. Experiments using both synthetic and real datasets demonstrate the value of the proposed approach.