An Extendable Python Implementation of Robust Optimisation Monte Carlo

Performing inference in statistical models with an intractable likelihood is challenging, therefore, most likelihood-free inference (LFI) methods encounter accuracy and efficiency limitations. In this paper, we present the implementation of the LFI method Robust Optimisation Monte Carlo (ROMC) in the Python package ELFI. ROMC is a novel and efficient (highly-parallelizable) LFI framework that provides accurate weighted samples from the posterior. Our implementation can be used in two ways. First, a scientist may use it as an out-of-the-box LFI algorithm; we provide an easy-to-use API harmonized with the principles of ELFI, enabling effortless comparisons with the rest of the methods included in the package. Additionally, we have carefully split ROMC into isolated components for supporting extensibility. A researcher may experiment with novel method(s) for solving part(s) of ROMC without reimplementing everything from scratch. In both scenarios, the ROMC parts can run in a fully-parallelized manner, exploiting all CPU cores. We also provide helpful functionalities for (i) inspecting the inference process and (ii) evaluating the obtained samples. Finally, we test the robustness of our implementation on some typical LFI examples.

Likelihood-Free Inference in State-Space Models with Unknown Dynamics

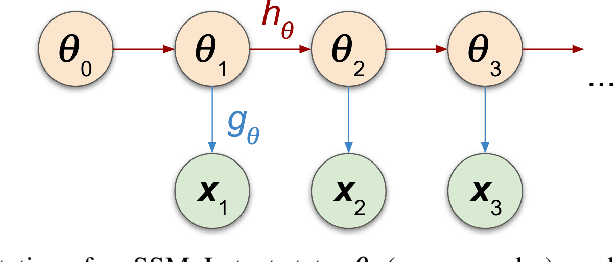
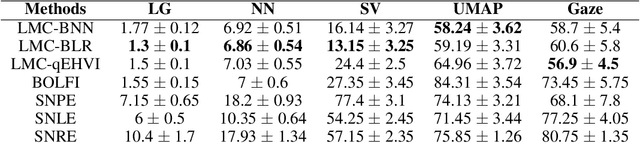
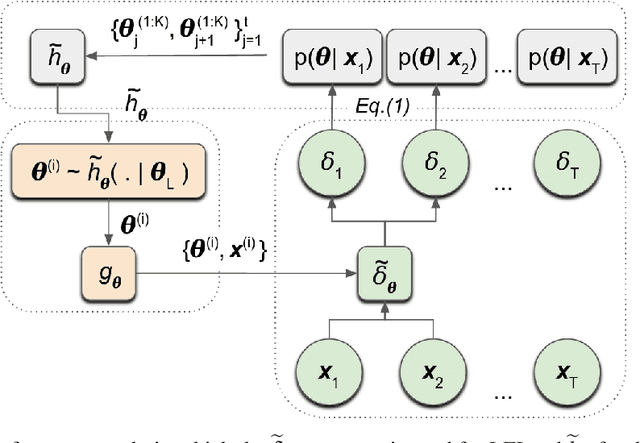
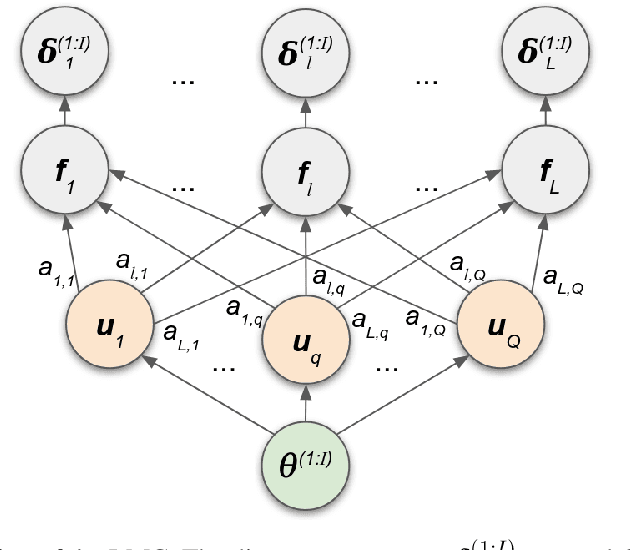
We introduce a method for inferring and predicting latent states in the important and difficult case of state-space models where observations can only be simulated, and transition dynamics are unknown. In this setting, the likelihood of observations is not available and only synthetic observations can be generated from a black-box simulator. We propose a way of doing likelihood-free inference (LFI) of states and state prediction with a limited number of simulations. Our approach uses a multi-output Gaussian process for state inference, and a Bayesian Neural Network as a model of the transition dynamics for state prediction. We improve upon existing LFI methods for the inference task, while also accurately learning transition dynamics. The proposed method is necessary for modelling inverse problems in dynamical systems with computationally expensive simulations, as demonstrated in experiments with non-stationary user models.

Likelihood-Free Inference with Deep Gaussian Processes

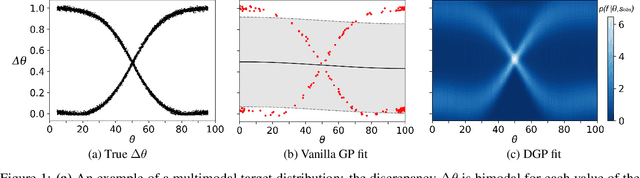
In recent years, surrogate models have been successfully used in likelihood-free inference to decrease the number of simulator evaluations. The current state-of-the-art performance for this task has been achieved by Bayesian Optimization with Gaussian Processes (GPs). While this combination works well for unimodal target distributions, it is restricting the flexibility and applicability of Bayesian Optimization for accelerating likelihood-free inference more generally. We address this problem by proposing a Deep Gaussian Process (DGP) surrogate model that can handle more irregularly behaved target distributions. Our experiments show how DGPs can outperform GPs on objective functions with multimodal distributions and maintain a comparable performance in unimodal cases. This confirms that DGPs as surrogate models can extend the applicability of Bayesian Optimization for likelihood-free inference (BOLFI), while adding computational overhead that remains negligible for computationally intensive simulators.

Split-BOLFI for for misspecification-robust likelihood free inference in high dimensions

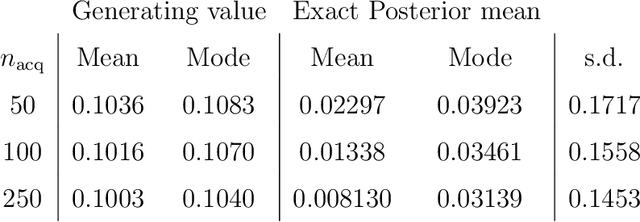
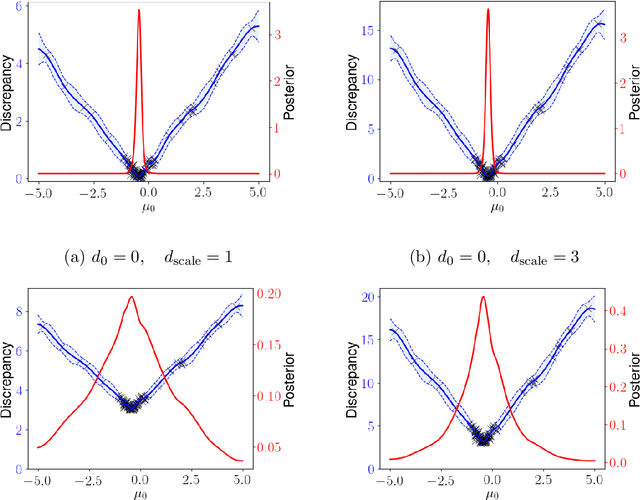
Likelihood-free inference for simulator-based statistical models has recently grown rapidly from its infancy to a useful tool for practitioners. However, models with more than a very small number of parameters as the target of inference have remained an enigma, in particular for the approximate Bayesian computation (ABC) community. To advance the possibilities for performing likelihood-free inference in high-dimensional parameter spaces, here we introduce an extension of the popular Bayesian optimisation based approach to approximate discrepancy functions in a probabilistic manner which lends itself to an efficient exploration of the parameter space. Our method achieves computational scalability by using separate acquisition procedures for the discrepancies defined for different parameters. These efficient high-dimensional simulation acquisitions are combined with exponentiated loss-likelihoods to provide a misspecification-robust characterisation of the marginal posterior distribution for all model parameters. The method successfully performs computationally efficient inference in a 100-dimensional space on canonical examples and compares favourably to existing Copula-ABC methods. We further illustrate the potential of this approach by fitting a bacterial transmission dynamics model to daycare centre data, which provides biologically coherent results on the strain competition in a 30-dimensional parameter space.

Approximate Bayesian Computation via Population Monte Carlo and Classification

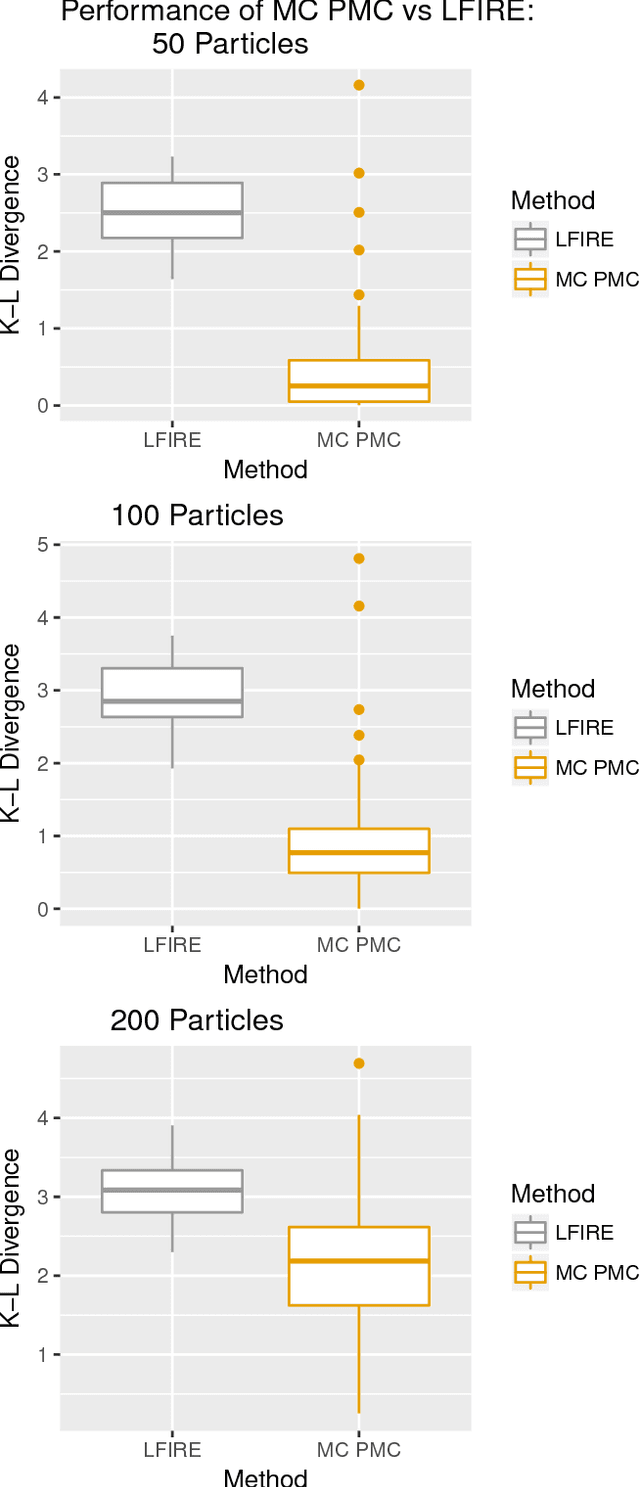
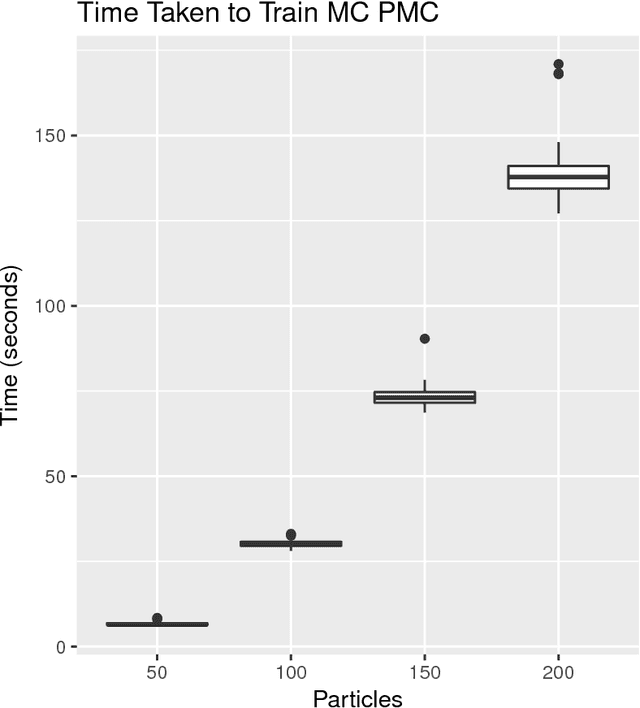
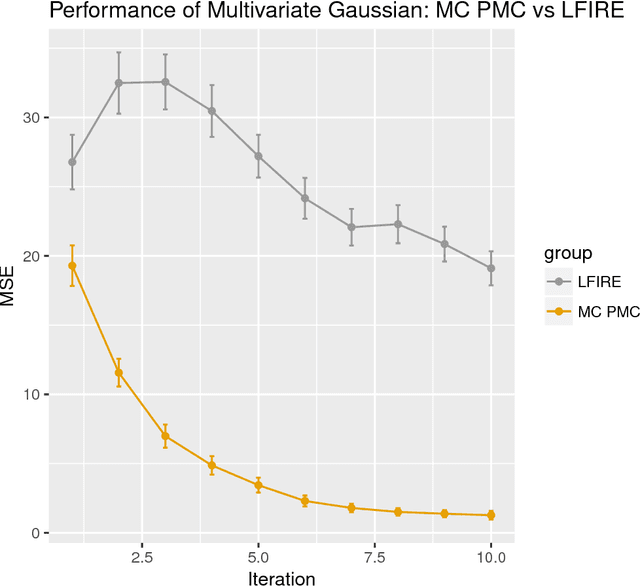
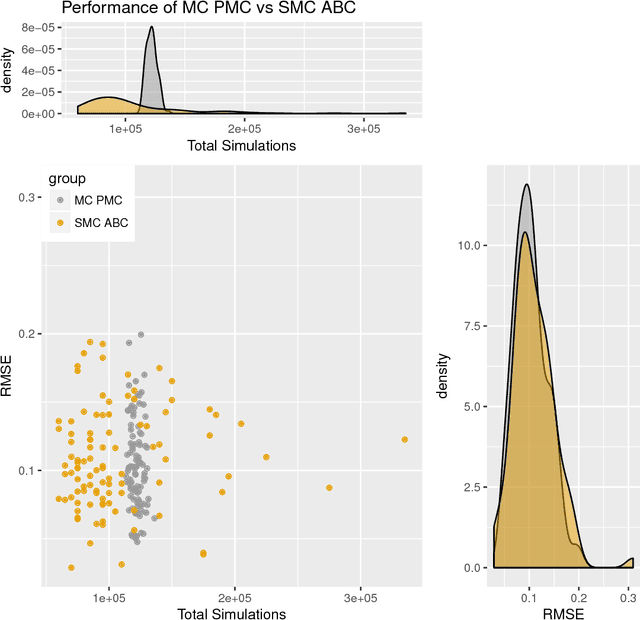
Approximate Bayesian computation (ABC) methods can be used to sample from posterior distributions when the likelihood function is unavailable or intractable, as is often the case in biological systems. Sequential Monte Carlo (SMC) methods have been combined with ABC to improve efficiency, however these approaches require many simulations from the likelihood. We propose a classification approach within a population Monte Carlo (PMC) framework, where model class probabilities are used to update the particle weights. Our proposed approach outperforms state-of-the-art ratio estimation methods while retaining the automatic selection of summary statistics, and performs competitively with SMC ABC.