Split-BOLFI for for misspecification-robust likelihood free inference in high dimensions

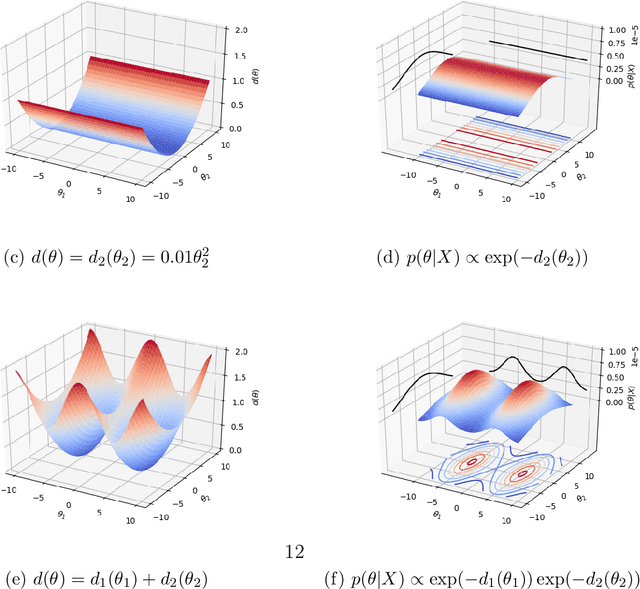
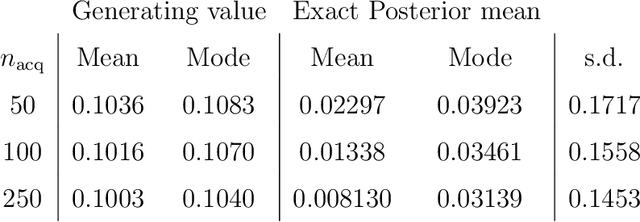
Likelihood-free inference for simulator-based statistical models has recently grown rapidly from its infancy to a useful tool for practitioners. However, models with more than a very small number of parameters as the target of inference have remained an enigma, in particular for the approximate Bayesian computation (ABC) community. To advance the possibilities for performing likelihood-free inference in high-dimensional parameter spaces, here we introduce an extension of the popular Bayesian optimisation based approach to approximate discrepancy functions in a probabilistic manner which lends itself to an efficient exploration of the parameter space. Our method achieves computational scalability by using separate acquisition procedures for the discrepancies defined for different parameters. These efficient high-dimensional simulation acquisitions are combined with exponentiated loss-likelihoods to provide a misspecification-robust characterisation of the marginal posterior distribution for all model parameters. The method successfully performs computationally efficient inference in a 100-dimensional space on canonical examples and compares favourably to existing Copula-ABC methods. We further illustrate the potential of this approach by fitting a bacterial transmission dynamics model to daycare centre data, which provides biologically coherent results on the strain competition in a 30-dimensional parameter space.

Diagnosing model misspecification and performing generalized Bayes' updates via probabilistic classifiers

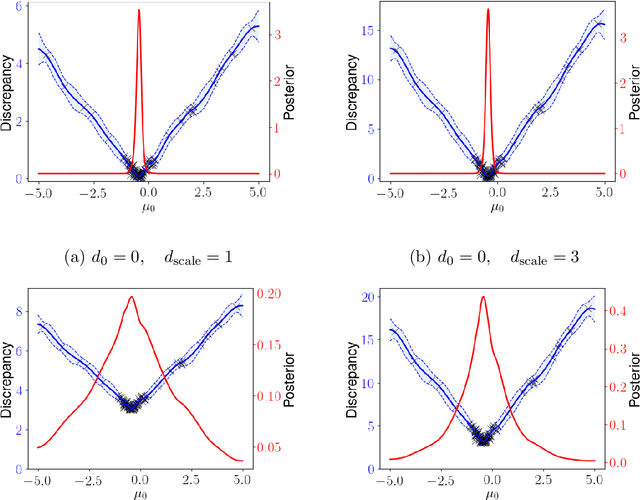
Model misspecification is a long-standing enigma of the Bayesian inference framework as posteriors tend to get overly concentrated on ill-informed parameter values towards the large sample limit. Tempering of the likelihood has been established as a safer way to do updates from prior to posterior in the presence of model misspecification. At one extreme tempering can ignore the data altogether and at the other extreme it provides the standard Bayes' update when no misspecification is assumed to be present. However, it is an open issue how to best recognize misspecification and choose a suitable level of tempering without access to the true generating model. Here we show how probabilistic classifiers can be employed to resolve this issue. By training a probabilistic classifier to discriminate between simulated and observed data provides an estimate of the ratio between the model likelihood and the likelihood of the data under the unobserved true generative process, within the discriminatory abilities of the classifier. The expectation of the logarithm of a ratio with respect to the data generating process gives an estimation of the negative Kullback-Leibler divergence between the statistical generative model and the true generative distribution. Using a set of canonical examples we show that this divergence provides a useful misspecification diagnostic, a model comparison tool, and a method to inform a generalised Bayesian update in the presence of misspecification for likelihood-based models.