Online simulator-based experimental design for cognitive model selection

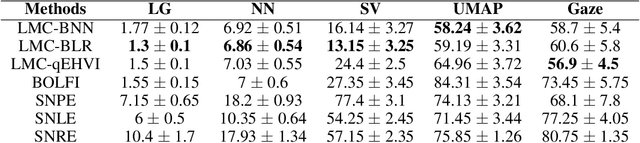
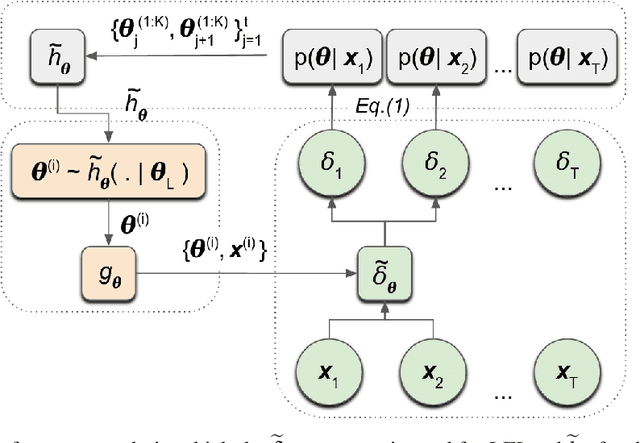
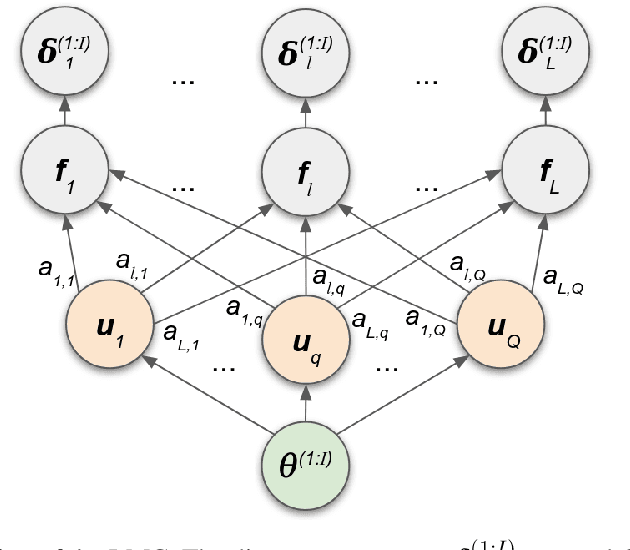
The problem of model selection with a limited number of experimental trials has received considerable attention in cognitive science, where the role of experiments is to discriminate between theories expressed as computational models. Research on this subject has mostly been restricted to optimal experiment design with analytically tractable models. However, cognitive models of increasing complexity, with intractable likelihoods, are becoming more commonplace. In this paper, we propose BOSMOS: an approach to experimental design that can select between computational models without tractable likelihoods. It does so in a data-efficient manner, by sequentially and adaptively generating informative experiments. In contrast to previous approaches, we introduce a novel simulator-based utility objective for design selection, and a new approximation of the model likelihood for model selection. In simulated experiments, we demonstrate that the proposed BOSMOS technique can accurately select models in up to 2 orders of magnitude less time than existing LFI alternatives for three cognitive science tasks: memory retention, sequential signal detection and risky choice.

Likelihood-Free Inference in State-Space Models with Unknown Dynamics

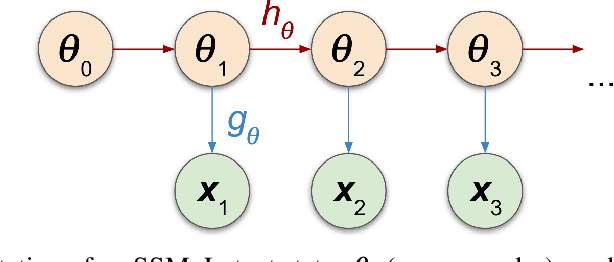
We introduce a method for inferring and predicting latent states in the important and difficult case of state-space models where observations can only be simulated, and transition dynamics are unknown. In this setting, the likelihood of observations is not available and only synthetic observations can be generated from a black-box simulator. We propose a way of doing likelihood-free inference (LFI) of states and state prediction with a limited number of simulations. Our approach uses a multi-output Gaussian process for state inference, and a Bayesian Neural Network as a model of the transition dynamics for state prediction. We improve upon existing LFI methods for the inference task, while also accurately learning transition dynamics. The proposed method is necessary for modelling inverse problems in dynamical systems with computationally expensive simulations, as demonstrated in experiments with non-stationary user models.

Likelihood-Free Inference with Deep Gaussian Processes

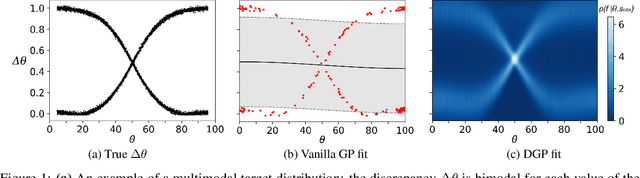
In recent years, surrogate models have been successfully used in likelihood-free inference to decrease the number of simulator evaluations. The current state-of-the-art performance for this task has been achieved by Bayesian Optimization with Gaussian Processes (GPs). While this combination works well for unimodal target distributions, it is restricting the flexibility and applicability of Bayesian Optimization for accelerating likelihood-free inference more generally. We address this problem by proposing a Deep Gaussian Process (DGP) surrogate model that can handle more irregularly behaved target distributions. Our experiments show how DGPs can outperform GPs on objective functions with multimodal distributions and maintain a comparable performance in unimodal cases. This confirms that DGPs as surrogate models can extend the applicability of Bayesian Optimization for likelihood-free inference (BOLFI), while adding computational overhead that remains negligible for computationally intensive simulators.