Approximate Bayesian inference from noisy likelihoods with Gaussian process emulated MCMC

We present an efficient approach for doing approximate Bayesian inference when only a limited number of noisy likelihood evaluations can be obtained due to computational constraints, which is becoming increasingly common for applications of complex models. Our main methodological innovation is to model the log-likelihood function using a Gaussian process (GP) in a local fashion and apply this model to emulate the progression that an exact Metropolis-Hastings (MH) algorithm would take if it was applicable. New log-likelihood evaluation locations are selected using sequential experimental design strategies such that each MH accept/reject decision is done within a pre-specified error tolerance. The resulting approach is conceptually simple and sample-efficient as it takes full advantage of the GP model. It is also more robust to violations of GP modelling assumptions and better suited for the typical situation where the posterior is substantially more concentrated than the prior, compared with various existing inference methods based on global GP surrogate modelling. We discuss the probabilistic interpretations and central theoretical aspects of our approach, and we then demonstrate the benefits of the resulting algorithm in the context of likelihood-free inference for simulator-based statistical models.

Batch simulations and uncertainty quantification in Gaussian process surrogate-based approximate Bayesian computation

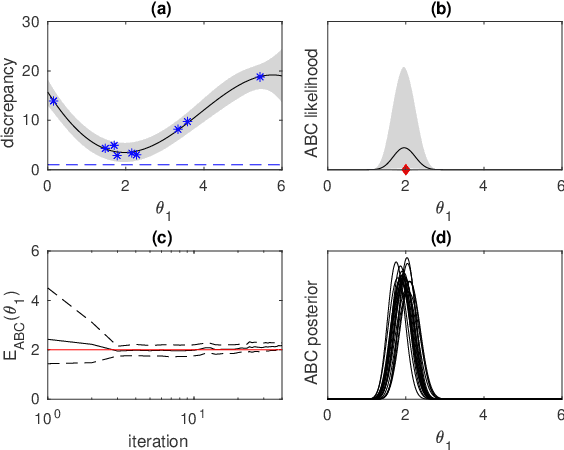
Surrogate models such as Gaussian processes (GP) have been proposed to accelerate approximate Bayesian computation (ABC) when the statistical model of interest is expensive-to-simulate. In one such promising framework the discrepancy between simulated and observed data is modelled with a GP. So far principled strategies have been proposed only for sequential selection of the simulation locations. To address this limitation, we develop Bayesian optimal design strategies to parallellise the expensive simulations. Current surrogate-based ABC methods also produce only a point estimate of the ABC posterior while there can be substantial additional uncertainty due to the limited budget of simulations. We also address the problem of quantifying the uncertainty of ABC posterior and discuss the connections between our resulting framework called Bayesian ABC, Bayesian quadrature (BQ) and Bayesian optimisation (BO). Experiments with several toy and real-world simulation models demonstrate advantages of the proposed techniques.

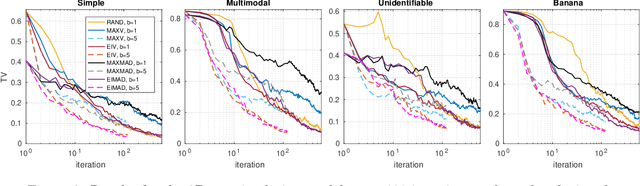
Parallel Gaussian process surrogate method to accelerate likelihood-free inference

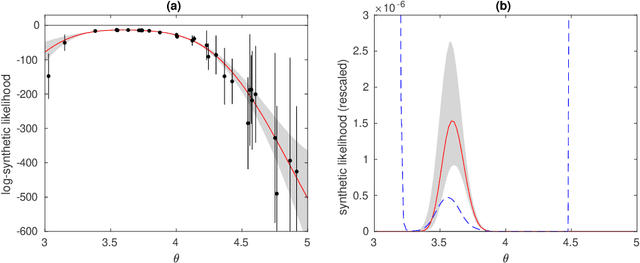
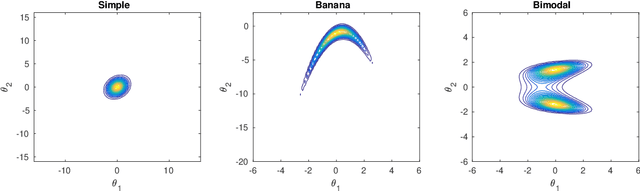
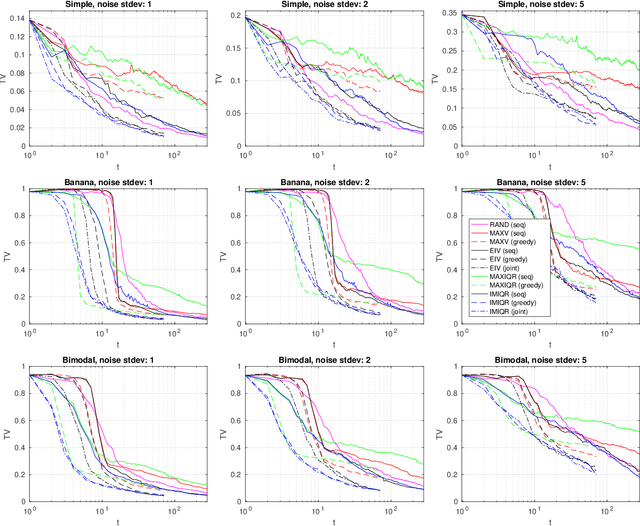
We consider Bayesian inference when only a limited number of noisy log-likelihood evaluations can be obtained. This occurs for example when complex simulator-based statistical models are fitted to data, and synthetic likelihood (SL) is used to form the noisy log-likelihood estimates using computationally costly forward simulations. We frame the inference task as a Bayesian sequential design problem, where the log-likelihood function is modelled with a hierarchical Gaussian process (GP) surrogate model, which is used to efficiently select additional log-likelihood evaluation locations. Motivated by recent progress in batch Bayesian optimisation, we develop various batch-sequential strategies where multiple simulations are adaptively selected to minimise either the expected or median loss function measuring the uncertainty in the resulting posterior. We analyse the properties of the resulting method theoretically and empirically. Experiments with toy problems and three simulation models suggest that our method is robust, highly parallelisable, and sample-efficient.

A Bayesian model of acquisition and clearance of bacterial colonization

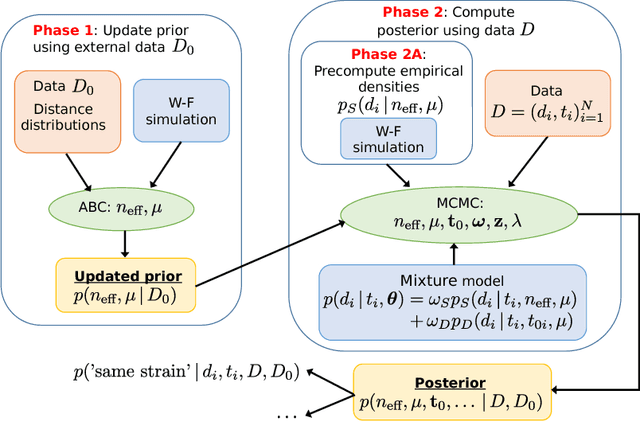
Bacterial populations that colonize a host play important roles in host health, including serving as a reservoir that transmits to other hosts and from which invasive strains emerge, thus emphasizing the importance of understanding rates of acquisition and clearance of colonizing populations. Studies of colonization dynamics have been based on assessment of whether serial samples represent a single population or distinct colonization events. A common solution to estimate acquisition and clearance rates is to use a fixed genetic distance threshold. However, this approach is often inadequate to account for the diversity of the underlying within-host evolving population, the time intervals between consecutive measurements, and the uncertainty in the estimated acquisition and clearance rates. Here, we summarize recently submitted work \cite{jarvenpaa2018named} and present a Bayesian model that provides probabilities of whether two strains should be considered the same, allowing to determine bacterial clearance and acquisition from genomes sampled over time. We explicitly model the within-host variation using population genetic simulation, and the inference is done by combining information from multiple data sources by using a combination of Approximate Bayesian Computation (ABC) and Markov Chain Monte Carlo (MCMC). We use the method to analyse a collection of methicillin resistant Staphylococcus aureus (MRSA) isolates.

Efficient acquisition rules for model-based approximate Bayesian computation

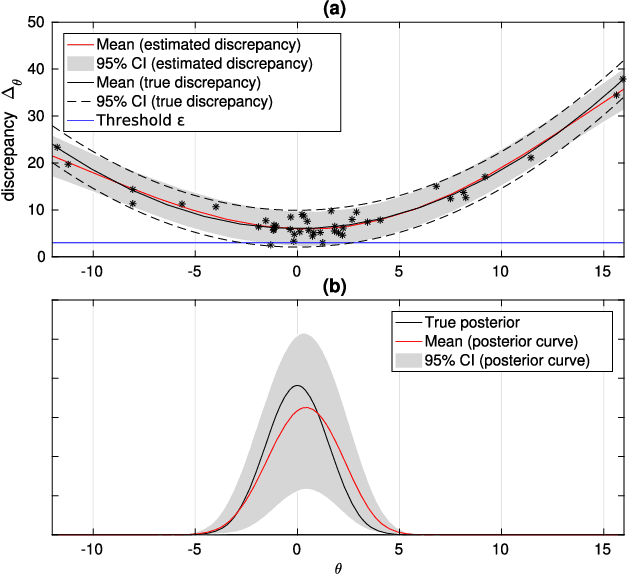
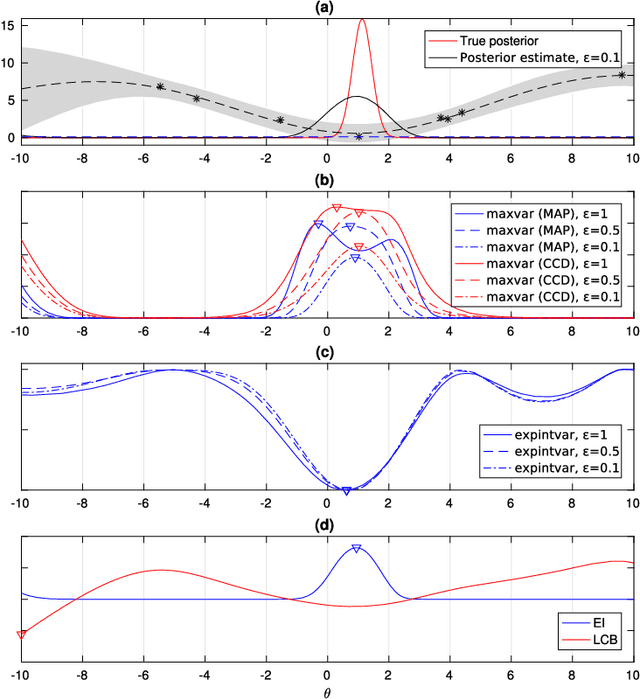
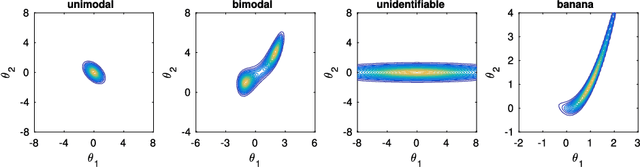
Approximate Bayesian computation (ABC) is a method for Bayesian inference when the likelihood is unavailable but simulating from the model is possible. However, many ABC algorithms require a large number of simulations, which can be costly. To reduce the computational cost, Bayesian optimisation (BO) and surrogate models such as Gaussian processes have been proposed. Bayesian optimisation enables one to intelligently decide where to evaluate the model next but common BO strategies are not designed for the goal of estimating the posterior distribution. Our paper addresses this gap in the literature. We propose to compute the uncertainty in the ABC posterior density, which is due to a lack of simulations to estimate this quantity accurately, and define a loss function that measures this uncertainty. We then propose to select the next evaluation location to minimise the expected loss. Experiments show that the proposed method often produces the most accurate approximations as compared to common BO strategies.

ELFI: Engine for Likelihood-Free Inference

Engine for Likelihood-Free Inference (ELFI) is a Python software library for performing likelihood-free inference (LFI). ELFI provides a convenient syntax for arranging components in LFI, such as priors, simulators, summaries or distances, to a network called ELFI graph. The components can be implemented in a wide variety of languages. The stand-alone ELFI graph can be used with any of the available inference methods without modifications. A central method implemented in ELFI is Bayesian Optimization for Likelihood-Free Inference (BOLFI), which has recently been shown to accelerate likelihood-free inference up to several orders of magnitude by surrogate-modelling the distance. ELFI also has an inbuilt support for output data storing for reuse and analysis, and supports parallelization of computation from multiple cores up to a cluster environment. ELFI is designed to be extensible and provides interfaces for widening its functionality. This makes the adding of new inference methods to ELFI straightforward and automatically compatible with the inbuilt features.

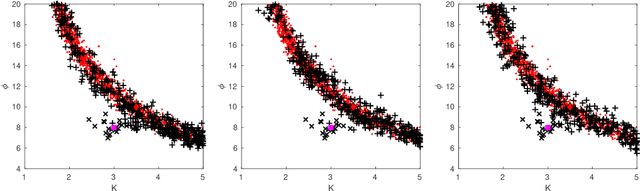
Gaussian process modeling in approximate Bayesian computation to estimate horizontal gene transfer in bacteria

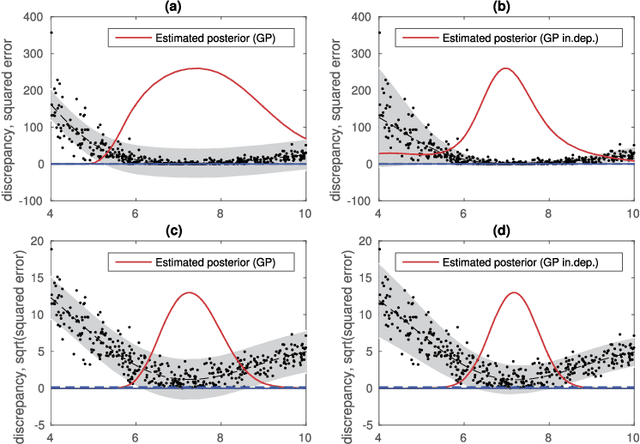
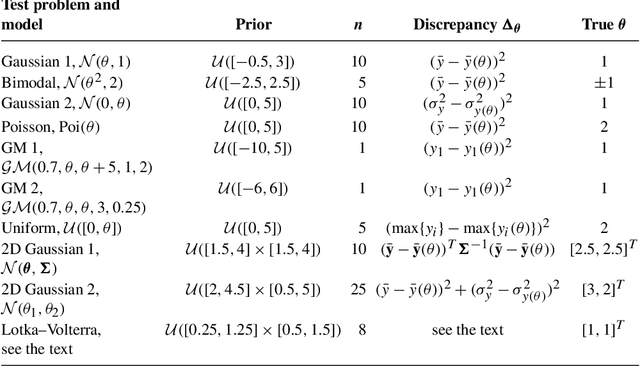
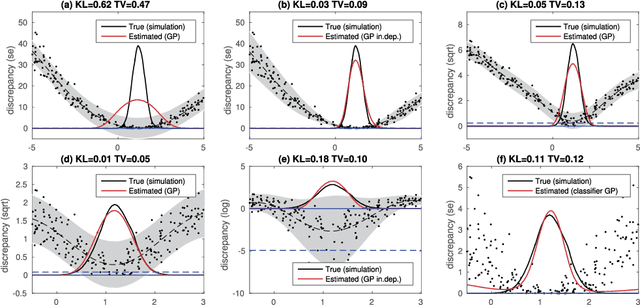
Approximate Bayesian computation (ABC) can be used for model fitting when the likelihood function is intractable but simulating from the model is feasible. However, even a single evaluation of a complex model may take several hours, limiting the number of model evaluations available. Modelling the discrepancy between the simulated and observed data using a Gaussian process (GP) can be used to reduce the number of model evaluations required by ABC, but the sensitivity of this approach to a specific GP formulation has not yet been thoroughly investigated. We begin with a comprehensive empirical evaluation of using GPs in ABC, including various transformations of the discrepancies and two novel GP formulations. Our results indicate the choice of GP may significantly affect the accuracy of the estimated posterior distribution. Selection of an appropriate GP model is thus important. We formulate expected utility to measure the accuracy of classifying discrepancies below or above the ABC threshold, and show that it can be used to automate the GP model selection step. Finally, based on the understanding gained with toy examples, we fit a population genetic model for bacteria, providing insight into horizontal gene transfer events within the population and from external origins.