Batch simulations and uncertainty quantification in Gaussian process surrogate-based approximate Bayesian computation

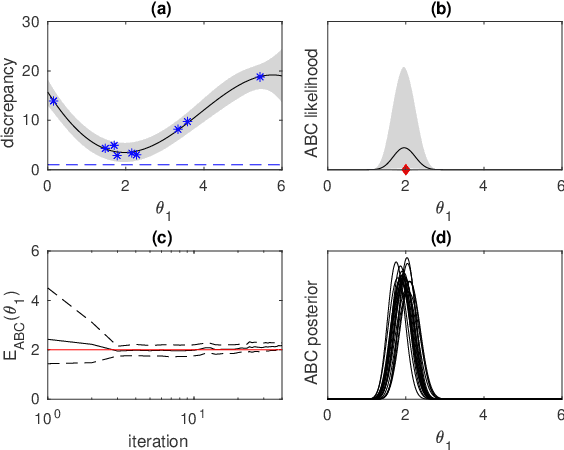
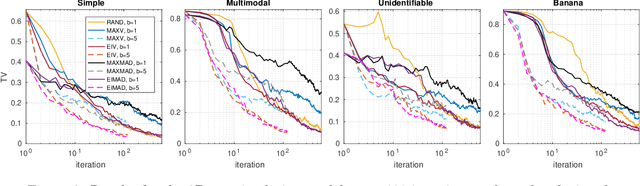
Surrogate models such as Gaussian processes (GP) have been proposed to accelerate approximate Bayesian computation (ABC) when the statistical model of interest is expensive-to-simulate. In one such promising framework the discrepancy between simulated and observed data is modelled with a GP. So far principled strategies have been proposed only for sequential selection of the simulation locations. To address this limitation, we develop Bayesian optimal design strategies to parallellise the expensive simulations. Current surrogate-based ABC methods also produce only a point estimate of the ABC posterior while there can be substantial additional uncertainty due to the limited budget of simulations. We also address the problem of quantifying the uncertainty of ABC posterior and discuss the connections between our resulting framework called Bayesian ABC, Bayesian quadrature (BQ) and Bayesian optimisation (BO). Experiments with several toy and real-world simulation models demonstrate advantages of the proposed techniques.