Designing Optimal Behavioral Experiments Using Machine Learning

Computational models are powerful tools for understanding human cognition and behavior. They let us express our theories clearly and precisely, and offer predictions that can be subtle and often counter-intuitive. However, this same richness and ability to surprise means our scientific intuitions and traditional tools are ill-suited to designing experiments to test and compare these models. To avoid these pitfalls and realize the full potential of computational modeling, we require tools to design experiments that provide clear answers about what models explain human behavior and the auxiliary assumptions those models must make. Bayesian optimal experimental design (BOED) formalizes the search for optimal experimental designs by identifying experiments that are expected to yield informative data. In this work, we provide a tutorial on leveraging recent advances in BOED and machine learning to find optimal experiments for any kind of model that we can simulate data from, and show how by-products of this procedure allow for quick and straightforward evaluation of models and their parameters against real experimental data. As a case study, we consider theories of how people balance exploration and exploitation in multi-armed bandit decision-making tasks. We validate the presented approach using simulations and a real-world experiment. As compared to experimental designs commonly used in the literature, we show that our optimal designs more efficiently determine which of a set of models best account for individual human behavior, and more efficiently characterize behavior given a preferred model. We provide code to replicate all analyses as well as tutorial notebooks and pointers to adapt the methodology to other experimental settings.

Domain Knowledge in A*-Based Causal Discovery

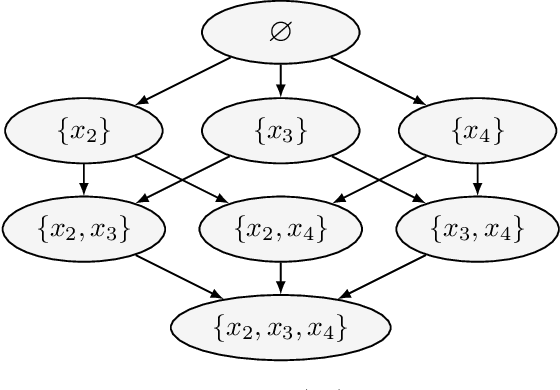
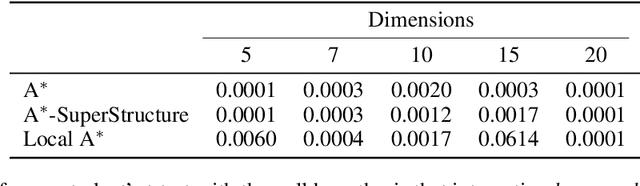
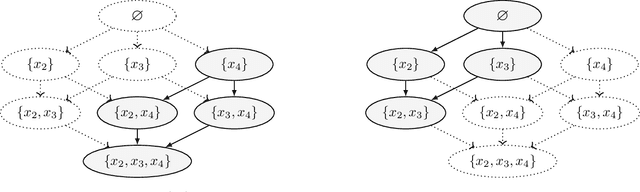
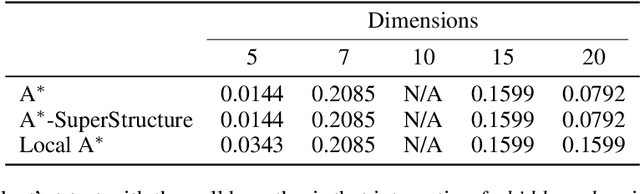
Causal discovery has become a vital tool for scientists and practitioners wanting to discover causal relationships from observational data. While most previous approaches to causal discovery have implicitly assumed that no expert domain knowledge is available, practitioners can often provide such domain knowledge from prior experience. Recent work has incorporated domain knowledge into constraint-based causal discovery. The majority of such constraint-based methods, however, assume causal faithfulness, which has been shown to be frequently violated in practice. Consequently, there has been renewed attention towards exact-search score-based causal discovery methods, which do not assume causal faithfulness, such as A*-based methods. However, there has been no consideration of these methods in the context of domain knowledge. In this work, we focus on efficiently integrating several types of domain knowledge into A*-based causal discovery. In doing so, we discuss and explain how domain knowledge can reduce the graph search space and then provide an analysis of the potential computational gains. We support these findings with experiments on synthetic and real data, showing that even small amounts of domain knowledge can dramatically speed up A*-based causal discovery and improve its performance and practicality.

Statistical applications of contrastive learning

The likelihood function plays a crucial role in statistical inference and experimental design. However, it is computationally intractable for several important classes of statistical models, including energy-based models and simulator-based models. Contrastive learning is an intuitive and computationally feasible alternative to likelihood-based learning. We here first provide an introduction to contrastive learning and then show how we can use it to derive methods for diverse statistical problems, namely parameter estimation for energy-based models, Bayesian inference for simulator-based models, as well as experimental design.

Implicit Deep Adaptive Design: Policy-Based Experimental Design without Likelihoods

We introduce implicit Deep Adaptive Design (iDAD), a new method for performing adaptive experiments in real-time with implicit models. iDAD amortizes the cost of Bayesian optimal experimental design (BOED) by learning a design policy network upfront, which can then be deployed quickly at the time of the experiment. The iDAD network can be trained on any model which simulates differentiable samples, unlike previous design policy work that requires a closed form likelihood and conditionally independent experiments. At deployment, iDAD allows design decisions to be made in milliseconds, in contrast to traditional BOED approaches that require heavy computation during the experiment itself. We illustrate the applicability of iDAD on a number of experiments, and show that it provides a fast and effective mechanism for performing adaptive design with implicit models.

Bayesian Optimal Experimental Design for Simulator Models of Cognition

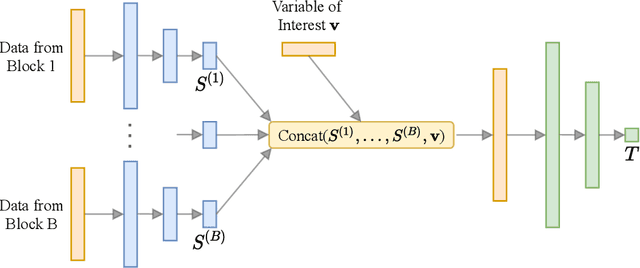
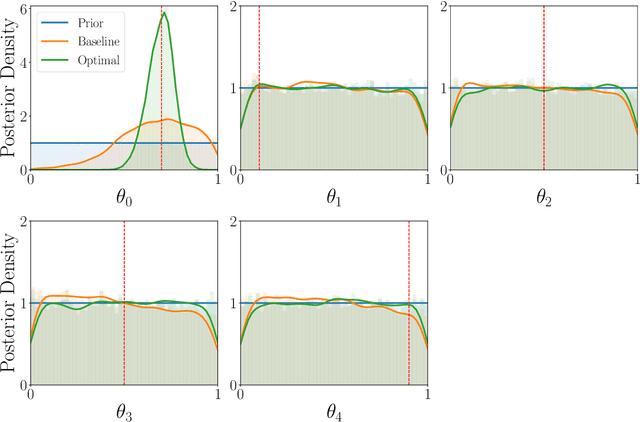
Bayesian optimal experimental design (BOED) is a methodology to identify experiments that are expected to yield informative data. Recent work in cognitive science considered BOED for computational models of human behavior with tractable and known likelihood functions. However, tractability often comes at the cost of realism; simulator models that can capture the richness of human behavior are often intractable. In this work, we combine recent advances in BOED and approximate inference for intractable models, using machine-learning methods to find optimal experimental designs, approximate sufficient summary statistics and amortized posterior distributions. Our simulation experiments on multi-armed bandit tasks show that our method results in improved model discrimination and parameter estimation, as compared to experimental designs commonly used in the literature.

Gradient-based Bayesian Experimental Design for Implicit Models using Mutual Information Lower Bounds

We introduce a framework for Bayesian experimental design (BED) with implicit models, where the data-generating distribution is intractable but sampling from it is still possible. In order to find optimal experimental designs for such models, our approach maximises mutual information lower bounds that are parametrised by neural networks. By training a neural network on sampled data, we simultaneously update network parameters and designs using stochastic gradient-ascent. The framework enables experimental design with a variety of prominent lower bounds and can be applied to a wide range of scientific tasks, such as parameter estimation, model discrimination and improving future predictions. Using a set of intractable toy models, we provide a comprehensive empirical comparison of prominent lower bounds applied to the aforementioned tasks. We further validate our framework on a challenging system of stochastic differential equations from epidemiology.

Sequential Bayesian Experimental Design for Implicit Models via Mutual Information

Bayesian experimental design (BED) is a framework that uses statistical models and decision making under uncertainty to optimise the cost and performance of a scientific experiment. Sequential BED, as opposed to static BED, considers the scenario where we can sequentially update our beliefs about the model parameters through data gathered in the experiment. A class of models of particular interest for the natural and medical sciences are implicit models, where the data generating distribution is intractable, but sampling from it is possible. Even though there has been a lot of work on static BED for implicit models in the past few years, the notoriously difficult problem of sequential BED for implicit models has barely been touched upon. We address this gap in the literature by devising a novel sequential design framework for parameter estimation that uses the Mutual Information (MI) between model parameters and simulated data as a utility function to find optimal experimental designs, which has not been done before for implicit models. Our approach uses likelihood-free inference by ratio estimation to simultaneously estimate posterior distributions and the MI. During the sequential BED procedure we utilise Bayesian optimisation to help us optimise the MI utility. We find that our framework is efficient for the various implicit models tested, yielding accurate parameter estimates after only a few iterations.

Bayesian Experimental Design for Implicit Models by Mutual Information Neural Estimation

Implicit stochastic models, where the data-generation distribution is intractable but sampling is possible, are ubiquitous in the natural sciences. The models typically have free parameters that need to be inferred from data collected in scientific experiments. A fundamental question is how to design the experiments so that the collected data are most useful. The field of Bayesian experimental design advocates that, ideally, we should choose designs that maximise the mutual information (MI) between the data and the parameters. For implicit models, however, this approach is severely hampered by the high computational cost of computing posteriors and maximising MI, in particular when we have more than a handful of design variables to optimise. In this paper, we propose a new approach to Bayesian experimental design for implicit models that leverages recent advances in neural MI estimation to deal with these issues. We show that training a neural network to maximise a lower bound on MI allows us to jointly determine the optimal design and the posterior. Simulation studies illustrate that this gracefully extends Bayesian experimental design for implicit models to higher design dimensions.

Efficient Bayesian Experimental Design for Implicit Models

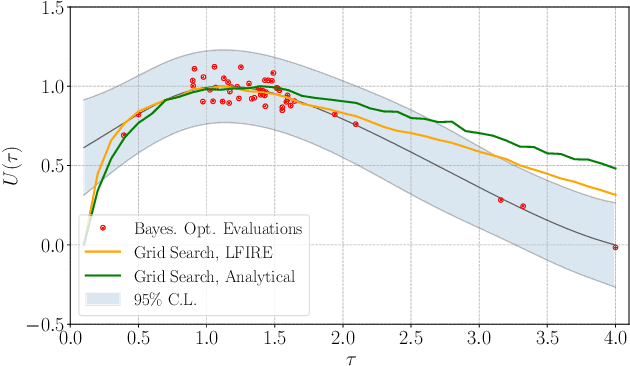
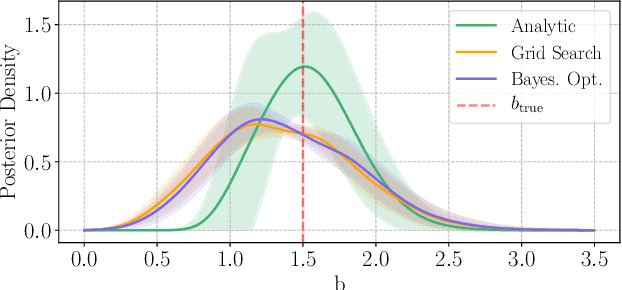
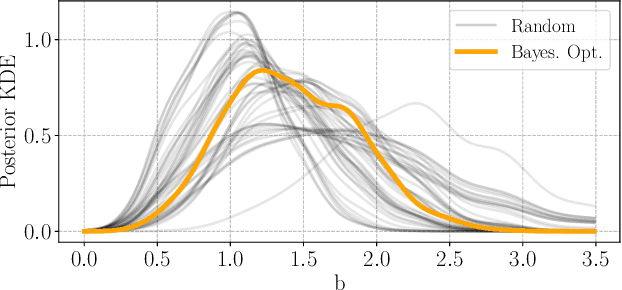
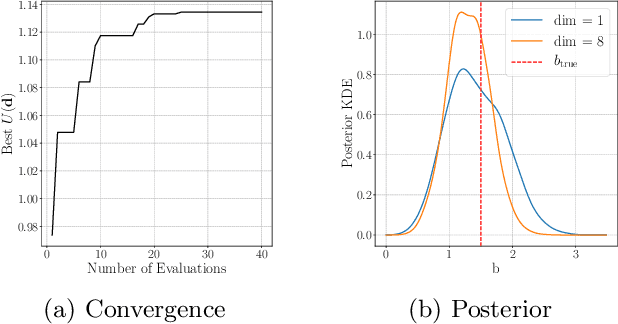
Bayesian experimental design involves the optimal allocation of resources in an experiment, with the aim of optimising cost and performance. For implicit models, where the likelihood is intractable but sampling from the model is possible, this task is particularly difficult and therefore largely unexplored. This is mainly due to technical difficulties associated with approximating posterior distributions and utility functions. We devise a novel experimental design framework for implicit models that improves upon previous work in two ways. First, we use the mutual information between parameters and data as the utility function, which has previously not been feasible. We achieve this by utilising Likelihood-Free Inference by Ratio Estimation (LFIRE) to approximate posterior distributions, instead of the traditional approximate Bayesian computation or synthetic likelihood methods. Secondly, we use Bayesian optimisation in order to solve the optimal design problem, as opposed to the typically used grid search. We find that this increases efficiency and allows us to consider higher design dimensions.