Equality of Effort via Algorithmic Recourse

This paper proposes a method for measuring fairness through equality of effort by applying algorithmic recourse through minimal interventions. Equality of effort is a property that can be quantified at both the individual and the group level. It answers the counterfactual question: what is the minimal cost for a protected individual or the average minimal cost for a protected group of individuals to reverse the outcome computed by an automated system? Algorithmic recourse increases the flexibility and applicability of the notion of equal effort: it overcomes its previous limitations by reconciling multiple treatment variables, introducing feasibility and plausibility constraints, and integrating the actual relative costs of interventions. We extend the existing definition of equality of effort and present an algorithm for its assessment via algorithmic recourse. We validate our approach both on synthetic data and on the German credit dataset.

Causal Analysis of the TOPCAT Trial: Spironolactone for Preserved Cardiac Function Heart Failure

We describe the results of applying causal discovery methods on the data from a multi-site clinical trial, on the Treatment of Preserved Cardiac Function Heart Failure with an Aldosterone Antagonist (TOPCAT). The trial was inconclusive, with no clear benefits consistently shown for the whole cohort. However, there were questions regarding the reliability of the diagnosis and treatment protocol for a geographic subgroup of the cohort. With the inclusion of medical context in the form of domain knowledge, causal discovery is used to demonstrate regional discrepancies and to frame the regional transportability of the results. Furthermore, we show that, globally and especially for some subgroups, the treatment has significant causal effects, thus offering a more refined view of the trial results.

Domain Knowledge in A*-Based Causal Discovery

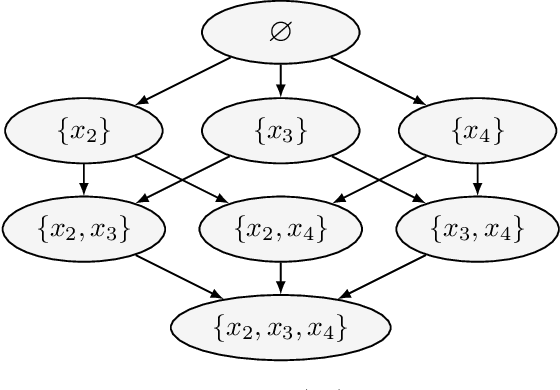
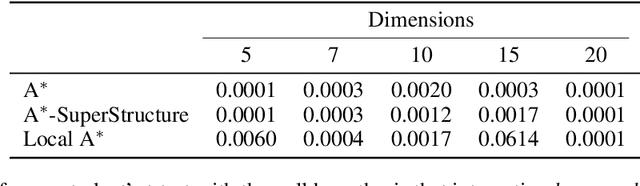
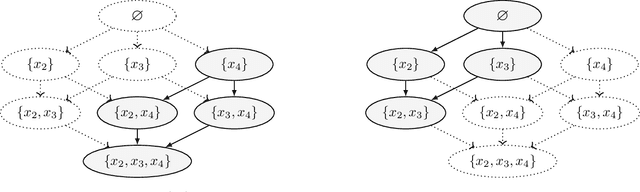
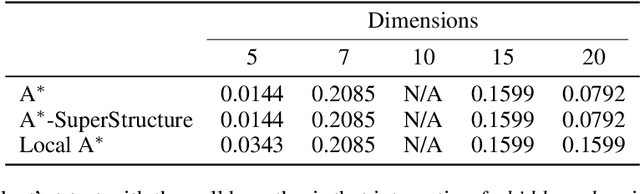
Causal discovery has become a vital tool for scientists and practitioners wanting to discover causal relationships from observational data. While most previous approaches to causal discovery have implicitly assumed that no expert domain knowledge is available, practitioners can often provide such domain knowledge from prior experience. Recent work has incorporated domain knowledge into constraint-based causal discovery. The majority of such constraint-based methods, however, assume causal faithfulness, which has been shown to be frequently violated in practice. Consequently, there has been renewed attention towards exact-search score-based causal discovery methods, which do not assume causal faithfulness, such as A*-based methods. However, there has been no consideration of these methods in the context of domain knowledge. In this work, we focus on efficiently integrating several types of domain knowledge into A*-based causal discovery. In doing so, we discuss and explain how domain knowledge can reduce the graph search space and then provide an analysis of the potential computational gains. We support these findings with experiments on synthetic and real data, showing that even small amounts of domain knowledge can dramatically speed up A*-based causal discovery and improve its performance and practicality.

Data Generating Process to Evaluate Causal Discovery Techniques for Time Series Data

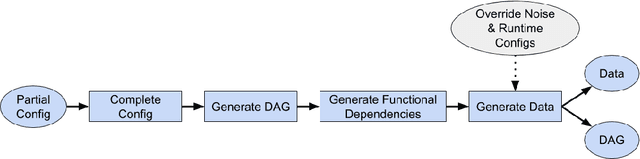
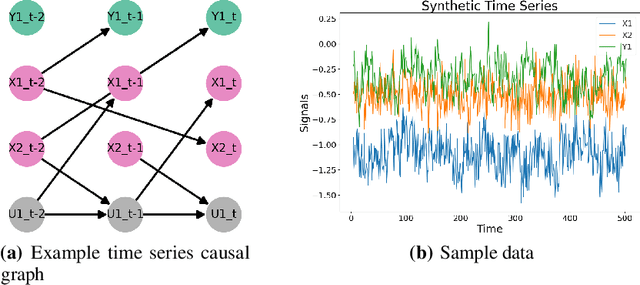
Going beyond correlations, the understanding and identification of causal relationships in observational time series, an important subfield of Causal Discovery, poses a major challenge. The lack of access to a well-defined ground truth for real-world data creates the need to rely on synthetic data for the evaluation of these methods. Existing benchmarks are limited in their scope, as they either are restricted to a "static" selection of data sets, or do not allow for a granular assessment of the methods' performance when commonly made assumptions are violated. We propose a flexible and simple to use framework for generating time series data, which is aimed at developing, evaluating, and benchmarking time series causal discovery methods. In particular, the framework can be used to fine tune novel methods on vast amounts of data, without "overfitting" them to a benchmark, but rather so they perform well in real-world use cases. Using our framework, we evaluate prominent time series causal discovery methods and demonstrate a notable degradation in performance when their assumptions are invalidated and their sensitivity to choice of hyperparameters. Finally, we propose future research directions and how our framework can support both researchers and practitioners.

DP-GP-LVM: A Bayesian Non-Parametric Model for Learning Multivariate Dependency Structures

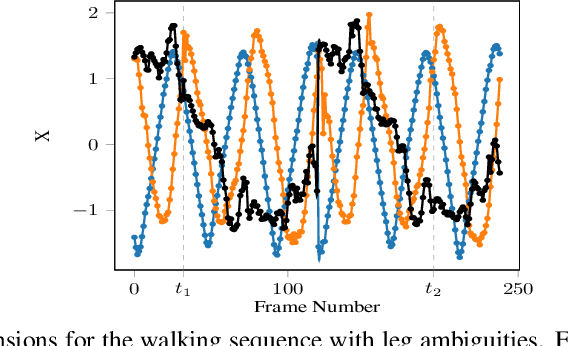
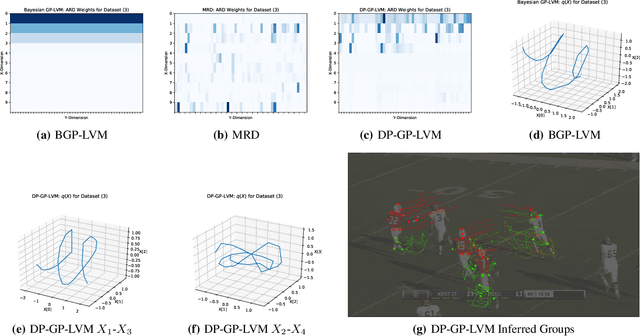
We present a non-parametric Bayesian latent variable model capable of learning dependency structures across dimensions in a multivariate setting. Our approach is based on flexible Gaussian process priors for the generative mappings and interchangeable Dirichlet process priors to learn the structure. The introduction of the Dirichlet process as a specific structural prior allows our model to circumvent issues associated with previous Gaussian process latent variable models. Inference is performed by deriving an efficient variational bound on the marginal log-likelihood on the model.