Partner Modelling Emerges in Recurrent Agents (But Only When It Matters)

Humans are remarkably adept at collaboration, able to infer the strengths and weaknesses of new partners in order to work successfully towards shared goals. To build AI systems with this capability, we must first understand its building blocks: does such flexibility require explicit, dedicated mechanisms for modelling others -- or can it emerge spontaneously from the pressures of open-ended cooperative interaction? To investigate this question, we train simple model-free RNN agents to collaborate with a population of diverse partners. Using the `Overcooked-AI' environment, we collect data from thousands of collaborative teams, and analyse agents' internal hidden states. Despite a lack of additional architectural features, inductive biases, or auxiliary objectives, the agents nevertheless develop structured internal representations of their partners' task abilities, enabling rapid adaptation and generalisation to novel collaborators. We investigated these internal models through probing techniques, and large-scale behavioural analysis. Notably, we find that structured partner modelling emerges when agents can influence partner behaviour by controlling task allocation. Our results show that partner modelling can arise spontaneously in model-free agents -- but only under environmental conditions that impose the right kind of social pressure.

Designing Optimal Behavioral Experiments Using Machine Learning

Computational models are powerful tools for understanding human cognition and behavior. They let us express our theories clearly and precisely, and offer predictions that can be subtle and often counter-intuitive. However, this same richness and ability to surprise means our scientific intuitions and traditional tools are ill-suited to designing experiments to test and compare these models. To avoid these pitfalls and realize the full potential of computational modeling, we require tools to design experiments that provide clear answers about what models explain human behavior and the auxiliary assumptions those models must make. Bayesian optimal experimental design (BOED) formalizes the search for optimal experimental designs by identifying experiments that are expected to yield informative data. In this work, we provide a tutorial on leveraging recent advances in BOED and machine learning to find optimal experiments for any kind of model that we can simulate data from, and show how by-products of this procedure allow for quick and straightforward evaluation of models and their parameters against real experimental data. As a case study, we consider theories of how people balance exploration and exploitation in multi-armed bandit decision-making tasks. We validate the presented approach using simulations and a real-world experiment. As compared to experimental designs commonly used in the literature, we show that our optimal designs more efficiently determine which of a set of models best account for individual human behavior, and more efficiently characterize behavior given a preferred model. We provide code to replicate all analyses as well as tutorial notebooks and pointers to adapt the methodology to other experimental settings.

Building Object-based Causal Programs for Human-like Generalization

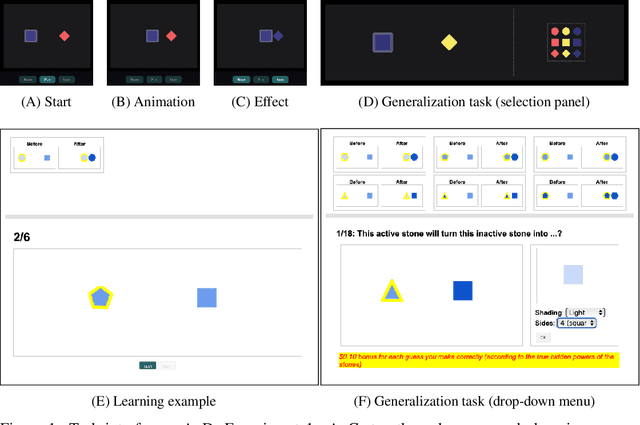
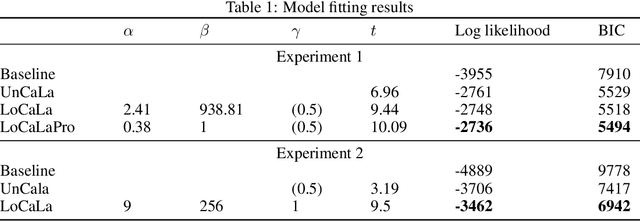
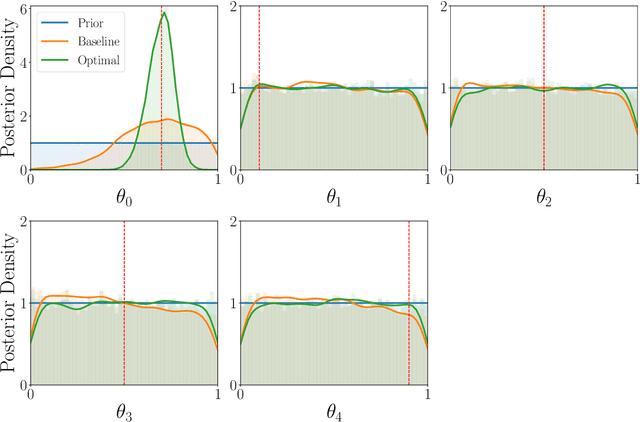
We present a novel task that measures how people generalize objects' causal powers based on observing a single (Experiment 1) or a few (Experiment 2) causal interactions between object pairs. We propose a computational modeling framework that can synthesize human-like generalization patterns in our task setting, and sheds light on how people may navigate the compositional space of possible causal functions and categories efficiently. Our modeling framework combines a causal function generator that makes use of agent and recipient objects' features and relations, and a Bayesian non-parametric inference process to govern the degree of similarity-based generalization. Our model has a natural "resource-rational" variant that outperforms a naive Bayesian account in describing participants, in particular reproducing a generalization-order effect and causal asymmetry observed in our behavioral experiments. We argue that this modeling framework provides a computationally plausible mechanism for real world causal generalization.

Bayesian Optimal Experimental Design for Simulator Models of Cognition

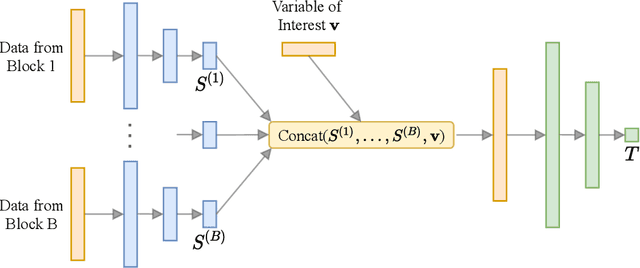
Bayesian optimal experimental design (BOED) is a methodology to identify experiments that are expected to yield informative data. Recent work in cognitive science considered BOED for computational models of human behavior with tractable and known likelihood functions. However, tractability often comes at the cost of realism; simulator models that can capture the richness of human behavior are often intractable. In this work, we combine recent advances in BOED and approximate inference for intractable models, using machine-learning methods to find optimal experimental designs, approximate sufficient summary statistics and amortized posterior distributions. Our simulation experiments on multi-armed bandit tasks show that our method results in improved model discrimination and parameter estimation, as compared to experimental designs commonly used in the literature.

Formalizing Neurath's Ship: Approximate Algorithms for Online Causal Learning

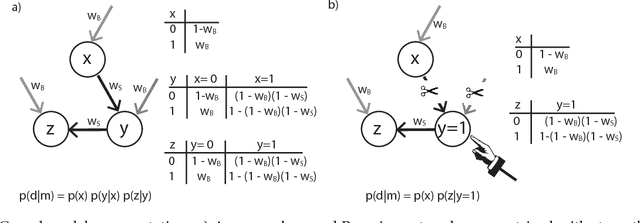
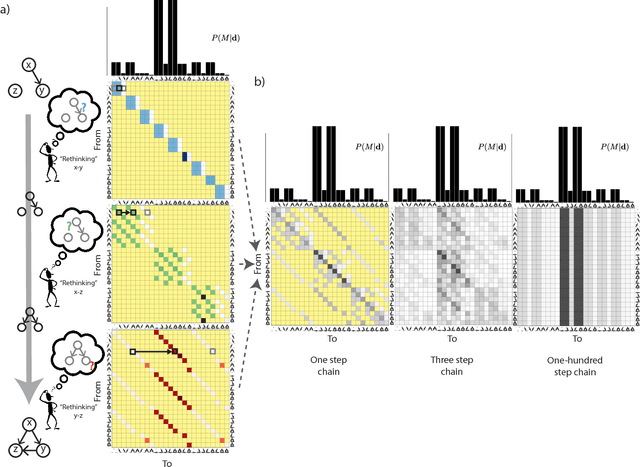
Higher-level cognition depends on the ability to learn models of the world. We can characterize this at the computational level as a structure-learning problem with the goal of best identifying the prevailing causal relationships among a set of relata. However, the computational cost of performing exact Bayesian inference over causal models grows rapidly as the number of relata increases. This implies that the cognitive processes underlying causal learning must be substantially approximate. A powerful class of approximations that focuses on the sequential absorption of successive inputs is captured by the Neurath's ship metaphor in philosophy of science, where theory change is cast as a stochastic and gradual process shaped as much by people's limited willingness to abandon their current theory when considering alternatives as by the ground truth they hope to approach. Inspired by this metaphor and by algorithms for approximating Bayesian inference in machine learning, we propose an algorithmic-level model of causal structure learning under which learners represent only a single global hypothesis that they update locally as they gather evidence. We propose a related scheme for understanding how, under these limitations, learners choose informative interventions that manipulate the causal system to help elucidate its workings. We find support for our approach in the analysis of four experiments.