CFMI: Flow Matching for Missing Data Imputation

We introduce conditional flow matching for imputation (CFMI), a new general-purpose method to impute missing data. The method combines continuous normalising flows, flow-matching, and shared conditional modelling to deal with intractabilities of traditional multiple imputation. Our comparison with nine classical and state-of-the-art imputation methods on 24 small to moderate-dimensional tabular data sets shows that CFMI matches or outperforms both traditional and modern techniques across a wide range of metrics. Applying the method to zero-shot imputation of time-series data, we find that it matches the accuracy of a related diffusion-based method while outperforming it in terms of computational efficiency. Overall, CFMI performs at least as well as traditional methods on lower-dimensional data while remaining scalable to high-dimensional settings, matching or exceeding the performance of other deep learning-based approaches, making it a go-to imputation method for a wide range of data types and dimensionalities.

Improving Variational Autoencoder Estimation from Incomplete Data with Mixture Variational Families

We consider the task of estimating variational autoencoders (VAEs) when the training data is incomplete. We show that missing data increases the complexity of the model's posterior distribution over the latent variables compared to the fully-observed case. The increased complexity may adversely affect the fit of the model due to a mismatch between the variational and model posterior distributions. We introduce two strategies based on (i) finite variational-mixture and (ii) imputation-based variational-mixture distributions to address the increased posterior complexity. Through a comprehensive evaluation of the proposed approaches, we show that variational mixtures are effective at improving the accuracy of VAE estimation from incomplete data.

Conditional Sampling of Variational Autoencoders via Iterated Approximate Ancestral Sampling

Conditional sampling of variational autoencoders (VAEs) is needed in various applications, such as missing data imputation, but is computationally intractable. A principled choice for asymptotically exact conditional sampling is Metropolis-within-Gibbs (MWG). However, we observe that the tendency of VAEs to learn a structured latent space, a commonly desired property, can cause the MWG sampler to get "stuck" far from the target distribution. This paper mitigates the limitations of MWG: we systematically outline the pitfalls in the context of VAEs, propose two original methods that address these pitfalls, and demonstrate an improved performance of the proposed methods on a set of sampling tasks.

Learning Job Titles Similarity from Noisy Skill Labels

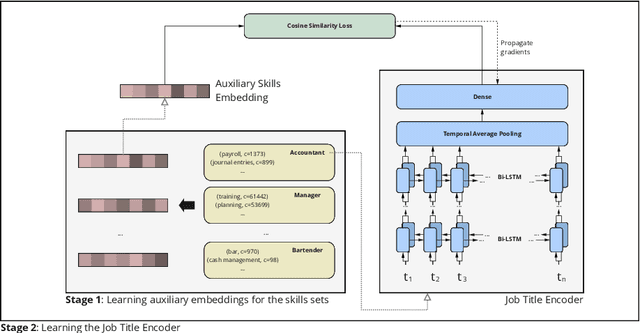
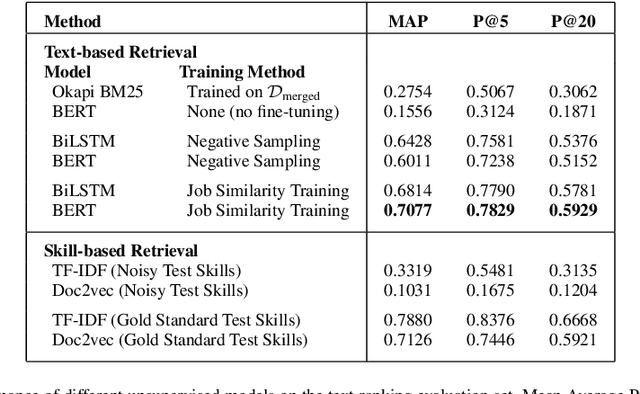
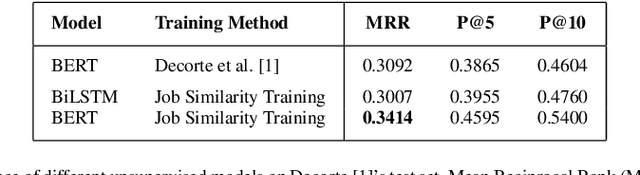
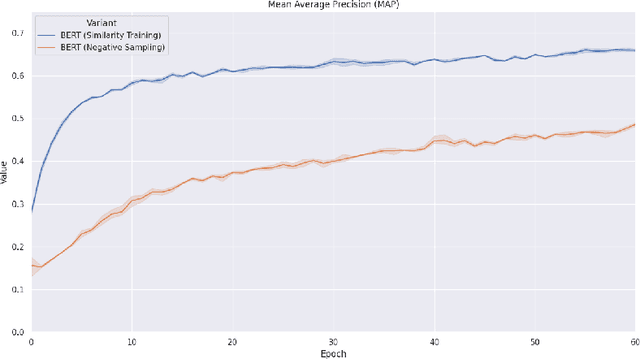
Measuring semantic similarity between job titles is an essential functionality for automatic job recommendations. This task is usually approached using supervised learning techniques, which requires training data in the form of equivalent job title pairs. In this paper, we instead propose an unsupervised representation learning method for training a job title similarity model using noisy skill labels. We show that it is highly effective for tasks such as text ranking and job normalization.

Variational Gibbs inference for statistical model estimation from incomplete data

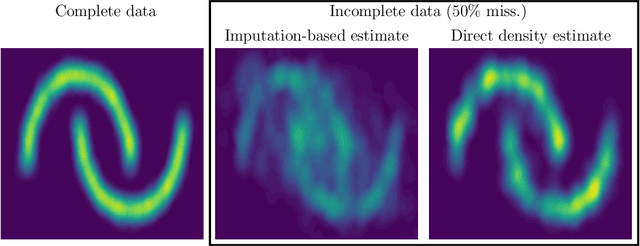
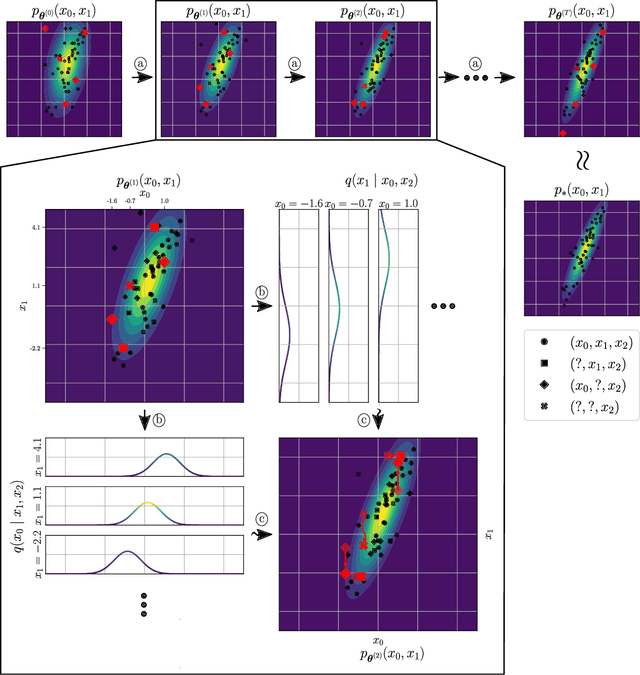
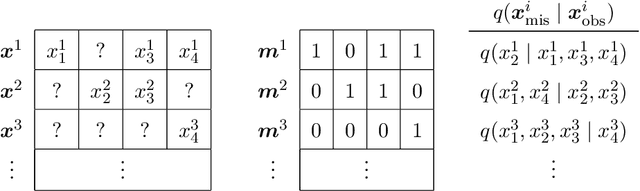
Statistical models are central to machine learning with broad applicability across a range of downstream tasks. The models are typically controlled by free parameters that are estimated from data by maximum-likelihood estimation. However, when faced with real-world datasets many of the models run into a critical issue: they are formulated in terms of fully-observed data, whereas in practice the datasets are plagued with missing data. The theory of statistical model estimation from incomplete data is conceptually similar to the estimation of latent-variable models, where powerful tools such as variational inference (VI) exist. However, in contrast to standard latent-variable models, parameter estimation with incomplete data often requires estimating exponentially-many conditional distributions of the missing variables, hence making standard VI methods intractable. We address this gap by introducing variational Gibbs inference (VGI), a new general-purpose method to estimate the parameters of statistical models from incomplete data. We validate VGI on a set of synthetic and real-world estimation tasks, estimating important machine learning models, VAEs and normalising flows, from incomplete data. The proposed method, whilst general-purpose, achieves competitive or better performance than existing model-specific estimation methods.