A Stochastic Bundle Method for Interpolating Networks
Paper and Code
Jan 29, 2022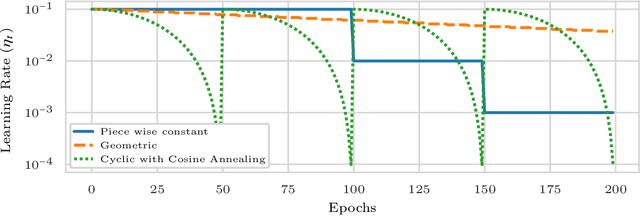
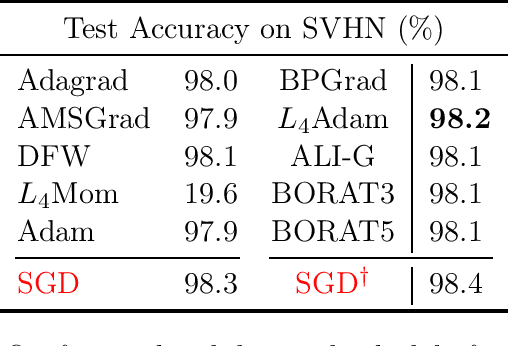
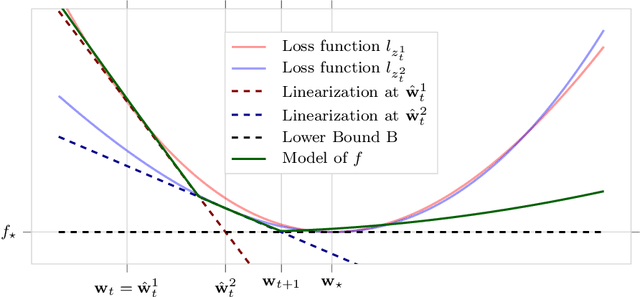
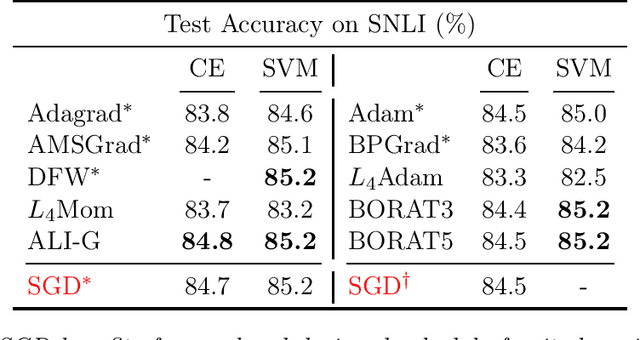
We propose a novel method for training deep neural networks that are capable of interpolation, that is, driving the empirical loss to zero. At each iteration, our method constructs a stochastic approximation of the learning objective. The approximation, known as a bundle, is a pointwise maximum of linear functions. Our bundle contains a constant function that lower bounds the empirical loss. This enables us to compute an automatic adaptive learning rate, thereby providing an accurate solution. In addition, our bundle includes linear approximations computed at the current iterate and other linear estimates of the DNN parameters. The use of these additional approximations makes our method significantly more robust to its hyperparameters. Based on its desirable empirical properties, we term our method Bundle Optimisation for Robust and Accurate Training (BORAT). In order to operationalise BORAT, we design a novel algorithm for optimising the bundle approximation efficiently at each iteration. We establish the theoretical convergence of BORAT in both convex and non-convex settings. Using standard publicly available data sets, we provide a thorough comparison of BORAT to other single hyperparameter optimisation algorithms. Our experiments demonstrate BORAT matches the state-of-the-art generalisation performance for these methods and is the most robust.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge