Learning Structure-from-Motion with Graph Attention Networks

In this paper we tackle the problem of learning Structure-from-Motion (SfM) through the use of graph attention networks. SfM is a classic computer vision problem that is solved though iterative minimization of reprojection errors, referred to as Bundle Adjustment (BA), starting from a good initialization. In order to obtain a good enough initialization to BA, conventional methods rely on a sequence of sub-problems (such as pairwise pose estimation, pose averaging or triangulation) which provides an initial solution that can then be refined using BA. In this work we replace these sub-problems by learning a model that takes as input the 2D keypoints detected across multiple views, and outputs the corresponding camera poses and 3D keypoint coordinates. Our model takes advantage of graph neural networks to learn SfM-specific primitives, and we show that it can be used for fast inference of the reconstruction for new and unseen sequences. The experimental results show that the proposed model outperforms competing learning-based methods, and challenges COLMAP while having lower runtime.

On the Tightness of Semidefinite Relaxations for Rotation Estimation

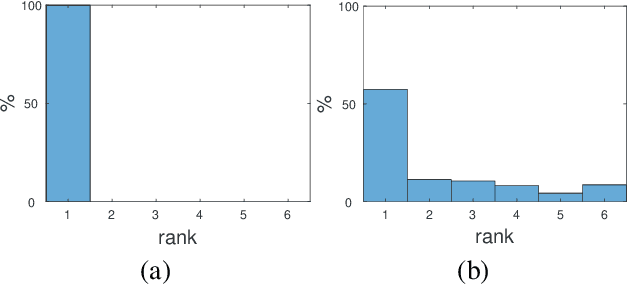
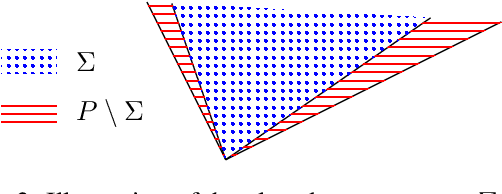
Why is it that semidefinite relaxations have been so successful in numerous applications in computer vision and robotics for solving non-convex optimization problems involving rotations? In studying the empirical performance, we note that there are hardly any failure cases reported in the literature, motivating us to approach these problems from a theoretical perspective. A general framework based on tools from algebraic geometry is introduced for analyzing the power of semidefinite relaxations of problems with quadratic objective functions and rotational constraints. Applications include registration, hand-eye calibration, camera resectioning and rotation averaging. We characterize the extreme points, and show that there are plenty of failure cases for which the relaxation is not tight, even in the case of a single rotation. We also show that for some problem classes, an appropriate rotation parametrization guarantees tight relaxations. Our theoretical findings are accompanied with numerical simulations, providing further evidence and understanding of the results.

Monocular Depth Parameterizing Networks

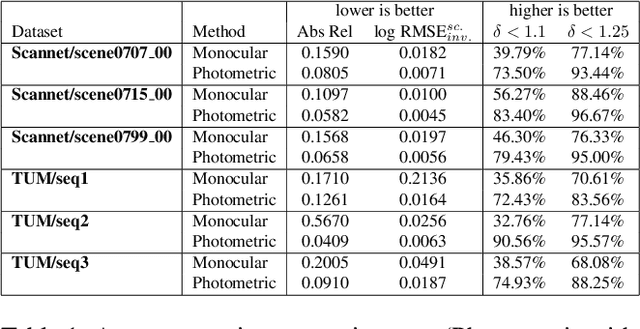
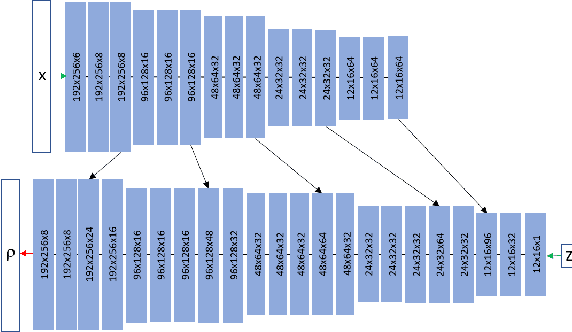
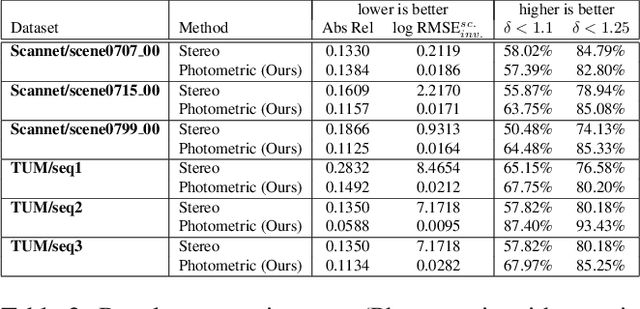
Monocular depth estimation is a highly challenging problem that is often addressed with deep neural networks. While these are able to use recognition of image features to predict reasonably looking depth maps the result often has low metric accuracy. In contrast traditional stereo methods using multiple cameras provide highly accurate estimation when pixel matching is possible. In this work we propose to combine the two approaches leveraging their respective strengths. For this purpose we propose a network structure that given an image provides a parameterization of a set of depth maps with feasible shapes. Optimizing over the parameterization then allows us to search the shapes for a photo consistent solution with respect to other images. This allows us to enforce geometric properties that are difficult to observe in single image as well as relaxes the learning problem allowing us to use relatively small networks. Our experimental evaluation shows that our method generates more accurate depth maps and generalizes better than competing state-of-the-art approaches.

Accurate Optimization of Weighted Nuclear Norm for Non-Rigid Structure from Motion

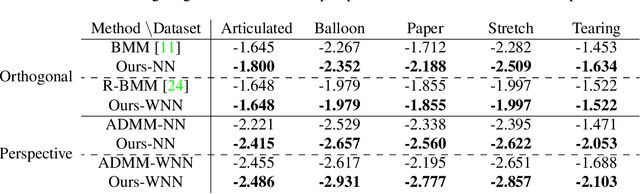
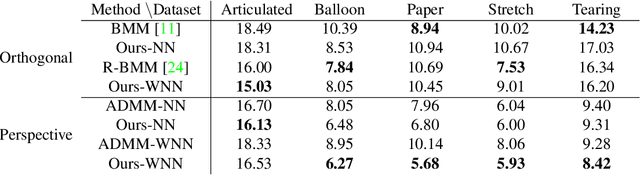
Fitting a matrix of a given rank to data in a least squares sense can be done very effectively using 2nd order methods such as Levenberg-Marquardt by explicitly optimizing over a bilinear parameterization of the matrix. In contrast, when applying more general singular value penalties, such as weighted nuclear norm priors, direct optimization over the elements of the matrix is typically used. Due to non-differentiability of the resulting objective function, first order sub-gradient or splitting methods are predominantly used. While these offer rapid iterations it is well known that they become inefficent near the minimum due to zig-zagging and in practice one is therefore often forced to settle for an approximate solution. In this paper we show that more accurate results can in many cases be achieved with 2nd order methods. Our main result shows how to construct bilinear formulations, for a general class of regularizers including weighted nuclear norm penalties, that are provably equivalent to the original problems. With these formulations the regularizing function becomes twice differentiable and 2nd order methods can be applied. We show experimentally, on a number of structure from motion problems, that our approach outperforms state-of-the-art methods.

Bilinear Parameterization For Differentiable Rank-Regularization

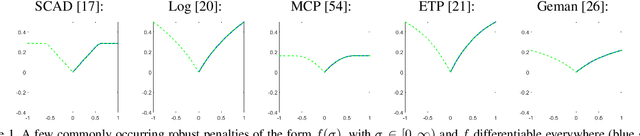
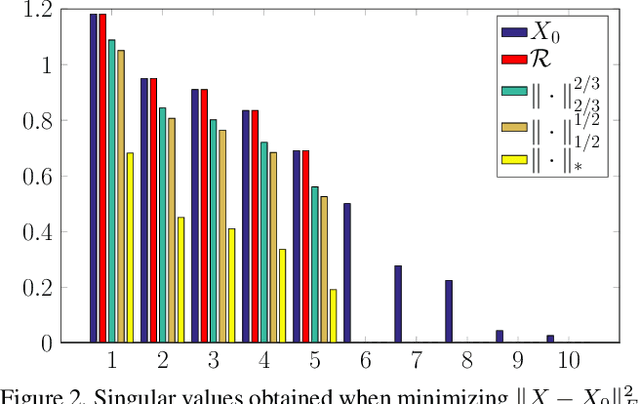
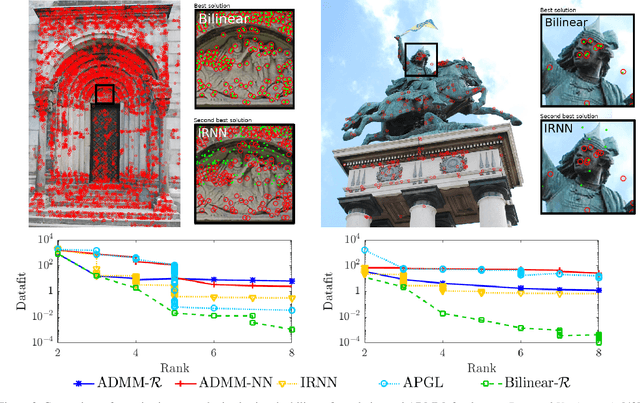
Low rank approximation is a commonly occurring problem in many computer vision and machine learning applications. There are two common ways of optimizing the resulting models. Either the set of matrices with a given sought rank can be explicitly parametrized using a bilinear factorization, or low rank can be implicitly enforced using regularization terms penalizing non-zero singular values. While the former results in differentiable problems that can be efficiently optimized using local quadratic approximation the latter are typically not differentiable (sometimes even discontinuous) and require splitting methods such as Alternating Direction Method of Multipliers (ADMM). It is well known that while ADMM makes rapid improvements the first couple of iterations convergence to the exact minimizer can be tediously slow. On the other hand regularization formulations can in certain cases come with theoretical optimality guarantees. In this paper we show how many non-differentiable regularization methods can be reformulated into smooth objectives using bilinear parameterization. This opens up the possibility of using second order methods such as Levenberg--Marquardt (LM) and Variable Projection (VarPro) to achieve accurate solutions for ill-conditioned problems. We show on several real and synthetic experiments that our second order formulation converges to substantially more accurate solutions than what ADMM formulations provide in a reasonable amount of time.

Rotation Averaging and Strong Duality

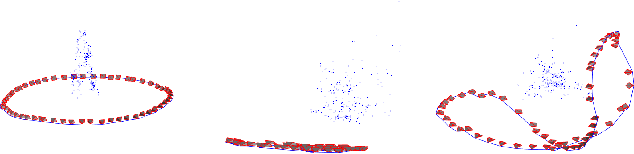
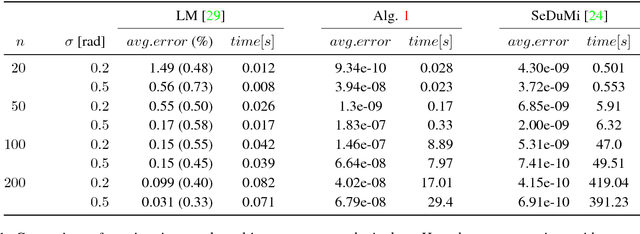
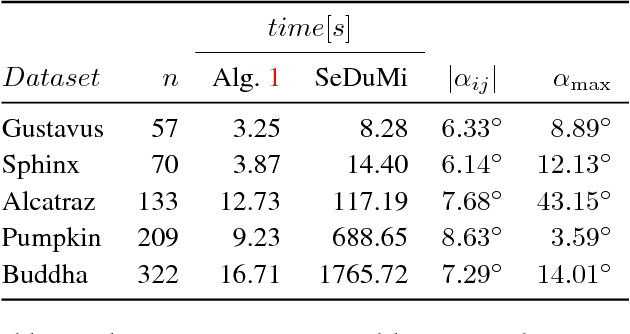
In this paper we explore the role of duality principles within the problem of rotation averaging, a fundamental task in a wide range of computer vision applications. In its conventional form, rotation averaging is stated as a minimization over multiple rotation constraints. As these constraints are non-convex, this problem is generally considered challenging to solve globally. We show how to circumvent this difficulty through the use of Lagrangian duality. While such an approach is well-known it is normally not guaranteed to provide a tight relaxation. Based on spectral graph theory, we analytically prove that in many cases there is no duality gap unless the noise levels are severe. This allows us to obtain certifiably global solutions to a class of important non-convex problems in polynomial time. We also propose an efficient, scalable algorithm that out-performs general purpose numerical solvers and is able to handle the large problem instances commonly occurring in structure from motion settings. The potential of this proposed method is demonstrated on a number of different problems, consisting of both synthetic and real-world data.

Volumetric Bias in Segmentation and Reconstruction: Secrets and Solutions

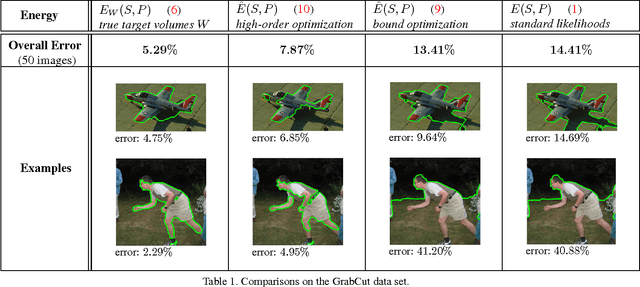
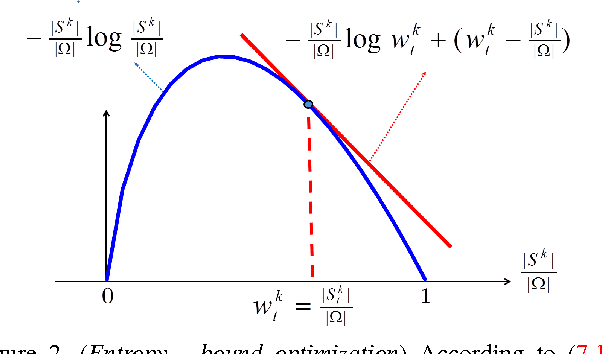
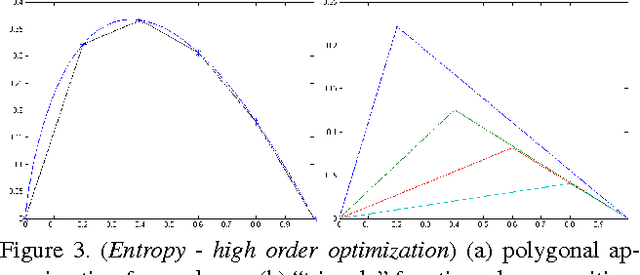
Many standard optimization methods for segmentation and reconstruction compute ML model estimates for appearance or geometry of segments, e.g. Zhu-Yuille 1996, Torr 1998, Chan-Vese 2001, GrabCut 2004, Delong et al. 2012. We observe that the standard likelihood term in these formulations corresponds to a generalized probabilistic K-means energy. In learning it is well known that this energy has a strong bias to clusters of equal size, which can be expressed as a penalty for KL divergence from a uniform distribution of cardinalities. However, this volumetric bias has been mostly ignored in computer vision. We demonstrate significant artifacts in standard segmentation and reconstruction methods due to this bias. Moreover, we propose binary and multi-label optimization techniques that either (a) remove this bias or (b) replace it by a KL divergence term for any given target volume distribution. Our general ideas apply to many continuous or discrete energy formulations in segmentation, stereo, and other reconstruction problems.

Simplifying Energy Optimization using Partial Enumeration

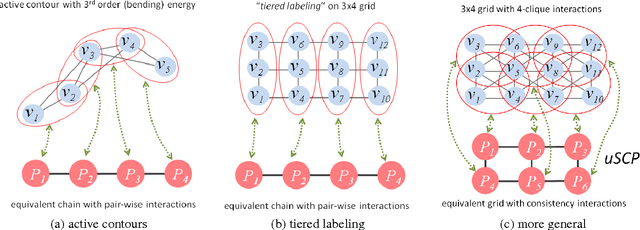
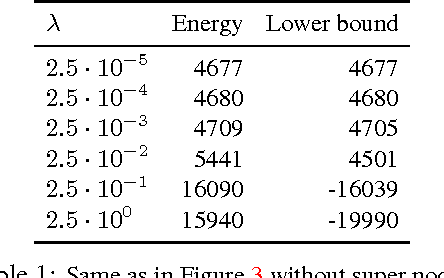
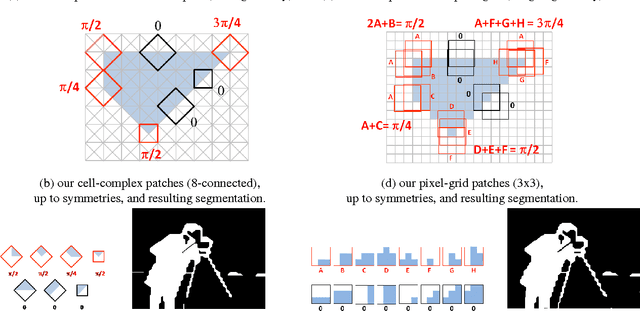
Energies with high-order non-submodular interactions have been shown to be very useful in vision due to their high modeling power. Optimization of such energies, however, is generally NP-hard. A naive approach that works for small problem instances is exhaustive search, that is, enumeration of all possible labelings of the underlying graph. We propose a general minimization approach for large graphs based on enumeration of labelings of certain small patches. This partial enumeration technique reduces complex high-order energy formulations to pairwise Constraint Satisfaction Problems with unary costs (uCSP), which can be efficiently solved using standard methods like TRW-S. Our approach outperforms a number of existing state-of-the-art algorithms on well known difficult problems (e.g. curvature regularization, stereo, deconvolution); it gives near global minimum and better speed. Our main application of interest is curvature regularization. In the context of segmentation, our partial enumeration technique allows to evaluate curvature directly on small patches using a novel integral geometry approach.